数据结构-归并排序

1、归并排序（Merge sort） 

是创建在归并操作上的一种有效的排序算法，时间复杂度为 O(n log n) 。1945年由约翰·冯·诺伊曼首次提出。该算法是采用 分治法（Divide and Conquer） 的一个非常典型的应用，且各层分治递归可以同时进行。

将已有序的子序列合并，得到完全有序的序列；即先使每个子序列有序，再使子序列段间有序。若将两个有序表合并成一个有序表，称为二路归并。

归并排序（MERGE-SORT）是利用归并的思想实现的排序方法，该算法采用经典的分治（divide-and-conquer）策略（分治法将问题分(divide)成一些小的问题然后递归求解，而治(conquer)的阶段则将分的阶段得到的各答案"修补"在一起，即分而治之)。

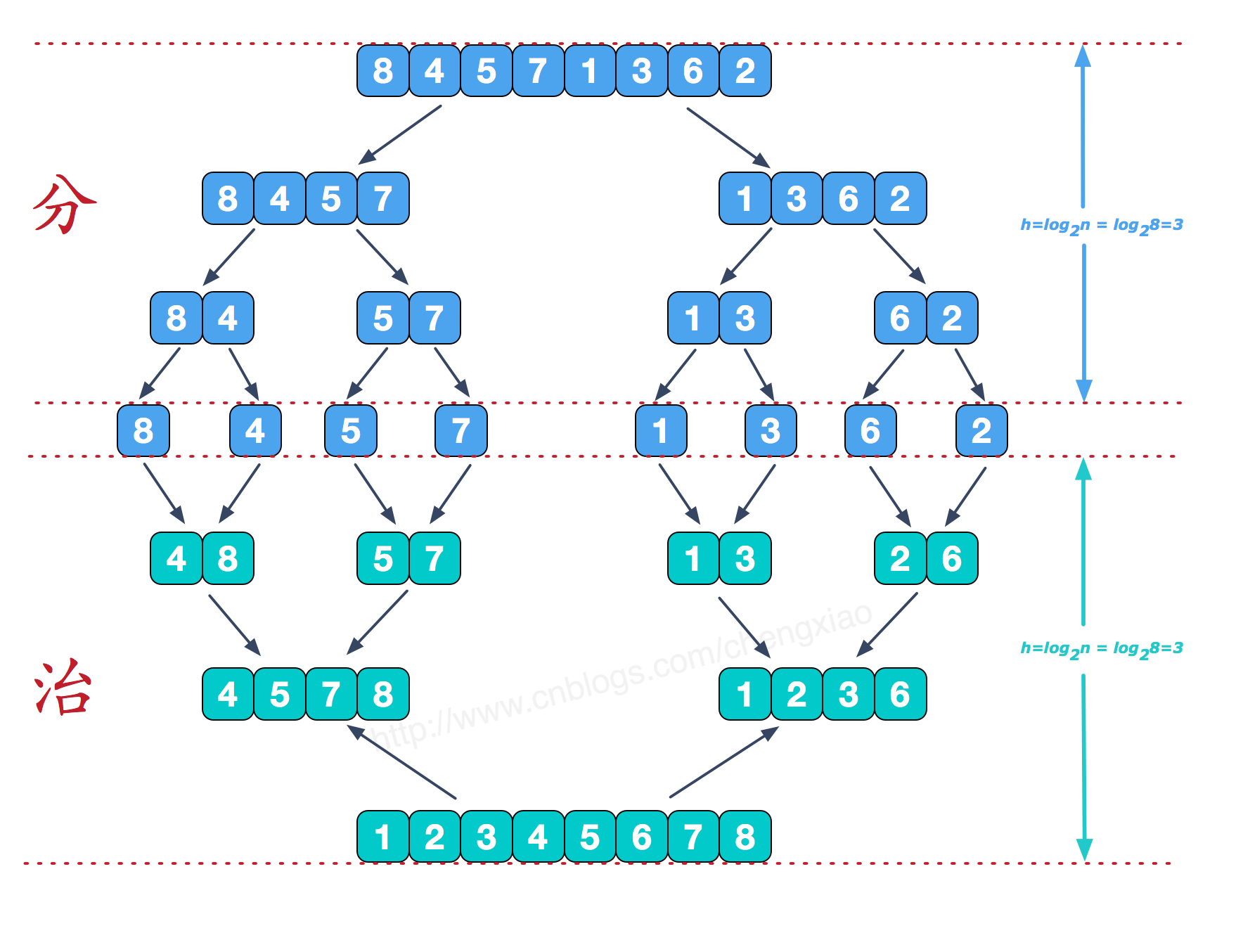
1、递归实现

（1）“分解”——将序列每次折半划分。
（2）“合并”——将划分后的序列段两两合并后排序。

#include <stdio.h>
#define Maxsize 10

void merge(int left[], int leftsize, int right[], int rightsize)
{
 int temp[Maxsize], i, j, k;
 i = j = k = 0;
 //对两个有序数组，进行合并，将最小的元素依次放入temp数组中
 while (i < leftsize && j < rightsize)
 {
  if (left[i] > right[j])
  {
   temp[k++] = right[j++];
  }
  else
  {
   temp[k++] = left[i++];
  }
 }
 //对未排放有序元素进行排放
 for (; i < leftsize; i++)
 {
  temp[k++] = left[i];
 }
 for (; j < rightsize; j++)
 {
  temp[k++] = right[j];
 }
 ////将局部变量数据存放入left[]中
 for (i = 0; i < (leftsize + rightsize); i++)
 {
  left[i] = temp[i];
 }
}

void MergeSort(int Arr[], int n)
{
 if (n > 1)
 {
  int* left = Arr;
  int leftsize = n / 2;
  int* right = Arr + leftsize;
  int rightsize = n - leftsize;

  MergeSort(left, leftsize);
  MergeSort(right, rightsize);

  merge(left, leftsize, right, rightsize);
 }
}

int main()
{
 int i;
 int a[10] = { 5, 2, 6, 0, 3, 9, 1, 7, 4, 8 };
 MergeSort(a, 10);

 for (i = 0; i < 10; i++)
  printf("%d ", a[i]);

 system("pause");
 return 0;
}

归并排序是稳定排序，它也是一种十分高效的排序，能利用完全二叉树特性的排序一般性能都不会太差。
从上文的图中可看出，每次合并操作的平均时间复杂度为O(n)，而完全二叉树的深度为|log2n|。总的平均时间复杂度为O(nlogn)。
而且，归并排序的最好，最坏，平均时间复杂度均为O(nlogn)。

用迭代方式实现归并排序的算法：

非递归的方法，避免了递归时深度为log2N的栈空间，空间只是用到归并临时申请的跟原来数组一样大小的空间，并且在时间性能上也有一定的提升，因此，使用归并排序是，尽量考虑用非递归的方法。

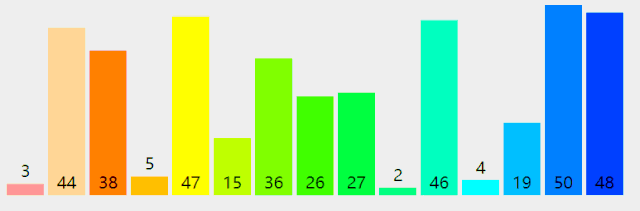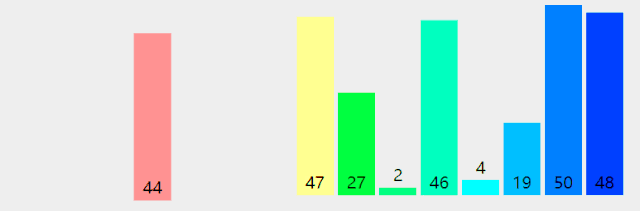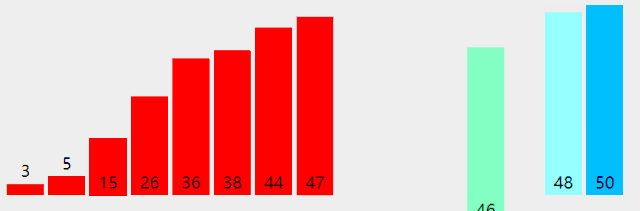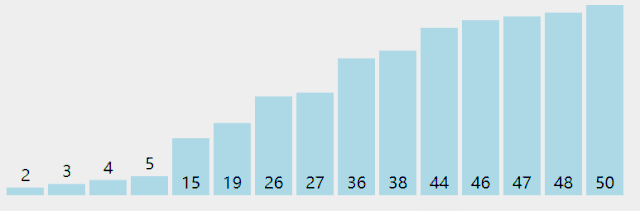
#include <stdio.h>
#define Maxsize 10


void MergeSort2(int k[], int n)
{
    int step, next, left_min, left_max, right_min, right_max;
    //开辟一个与原来数组一样大小的空间用来存储
    int* temp = (int*)malloc(sizeof(int) * n);
    //分组步长step逐级上升，第一次比较2个，然后4，8...
    for (step = 1; step < n; step *= 2)
    {
        //每个步长下，都是从0开始，数组的头元素开始
        for (left_min = 0; left_min < n - step; left_min = right_max)
        {
            //min指向的是要合并序列的第一个元素，max指向的是界限
            right_min = left_max = left_min + step;
            right_max = right_min + step;

            //最右边的下标只能为n
            if (right_max > n)
                right_max = n;

            //next是用来标志temp下标的，由于每次数据都会返回到k，故每次开始都会重新置零
            next = 0;
            //如果左边的数据还没有到达分割线且右边的数据也没有到达分割线，执行循环
            while (left_min < left_max && right_min < right_max)
            {
                if (k[left_min] < k[right_min])
                {
                    temp[next++] = k[left_min++];
                }
                else
                {
                    temp[next++] = k[right_min++];
                }
            }
            //上面循环结束的条件有两个，如果是左边的游标尚未到达，那么需要把
            //数组接回去，可能会有疑问，那如果右边的没到达呢，其实模拟一下就可以
            //知道，如果右边没到达，那么说明右边的数据比较大，这时也就不用移动位置了
            while (left_min < left_max)
            {
                //如果执行，则说明左边的序列数值要大，则现在需要将他们接在合并数组的最后面，从后先前排列
                k[--right_min] = k[--left_max];
            }
            //将合并的部分有序数组返回原数组
            while (next > 0)
            {
                k[--right_min] = temp[--next];
            }
        }
    }
}

int main()
{
    int i;
    int a[10] = { 5, 2, 6, 0, 3, 9, 1, 7, 4, 8 };
    //MergeSort(a, 10);
    MergeSort2(a, 10);
    for (i = 0; i < 10; i++)
        printf("%d ", a[i]);

    system("pause");
    return 0;
}

参考

参考

链表实现归并排序：

public class Hello {
    public  static  void  main(String [] args)
    {
       // System.out.println("Hello");
        Node head=new Node(5);
        Node p=head;
        for(int i=10;i>=0;i--)
        {
            Node q=new Node(i);
            p.next=q;
            p=q;

        }
        //head.next=new Node(1);
        //head.next.next=new Node(9);
        //head.toPrint();

        Hello s= new Hello();
        s.mergeSort(head).toPrint();
    }
    public  Node mergeSort(Node head){
        if(head==null)
            return  null;
        if(head.next==null)                     // 递归调用结束条件
            return  head;
        Node mid=findMiddle(head);              // 二分
        return merge(mergeSort(head),mergeSort(mid));   归并
    }

    private Node merge(Node p1, Node p2){
        Node dummy=new Node(-1);                // 定义头节点
        Node p=dummy;
        while(p1!=null && p2!=null)             // p1和p2相当于两个滑动指针
        {
            if(p1.val<p2.val)
            {
                p.next=p1;
                p1=p1.next;
            }
            else
            {
                p.next=p2;
                p2=p2.next;
            }
            p=p.next;
        }
        while(p1!=null)
        {
            p.next=p1;
            p1=p1.next;
            p=p.next;
        }
        while(p2!=null)
        {
            p.next=p2;
            p2=p2.next;
            p=p.next;
        }
        return  dummy.next;
    }

    private Node findMiddle(Node head){             //使用快慢指针对链表进行二分
        Node fast=head;
        Node slow=head;
        while(fast.next!=null && fast.next.next!=null){
            slow=slow.next;
            fast=fast.next.next;
        }
        Node mid=slow.next;                         // 将链表分为两部分
        slow.next=null;
        return  mid;

    }

    static class  Node{
        int val;
        Node next;
        Node(int val)
        {
            this.val=val;
        }
        void toPrint(){
            Node p=this;
            while(p!=null){
                System.out.println(p.val+" ");
                p=p.next;
            }
        }
    }


}

 

 

 

/*
public class ListNode {
    int val;
    ListNode next = null;

    ListNode(int val) {
        this.val = val;
    }
}*/
public class Solution {
    public ListNode Merge(ListNode p1,ListNode p2) {
        if(p1==null)
            return p2;
        if(p2==null)
            return p1;
         //新建一个头节点，用来存合并的链表。
        ListNode head=new ListNode(0);
        ListNode L=head;
        while(p1!=null && p2!=null)
        {
            if(p1.val<p2.val)
            {
                head.next=p1;
                p1=p1.next;
                head=head.next;
            }else{
                head.next=p2;
                p2=p2.next;
                head=head.next;

            }
        }
         //把未结束的链表连接到合并后的链表尾部
        while(p1!=null){
            head.next=p1;
            p1=p1.next;
            head=head.next;
        }
        while(p2!=null){
            head.next=p2;
            p2=p2.next;
            head=head.next;
        }
        return L.next;
    }
}