51Nod 1352 集合计数 扩展欧几里得

基准时间限制：1 秒 空间限制：131072 KB 分值: 20 难度：3级算法题
给出N个固定集合{1，N},{2,N-1},{3,N-2},...,{N-1,2},{N,1}.求出有多少个集合满足：第一个元素是A的倍数且第二个元素是B的倍数。
提示：
对于第二组测试数据，集合分别是：{1,10},{2,9},{3,8},{4,7},{5,6},{6,5},{7,4},{8,3},{9,2},{10,1}.满足条件的是第2个和第8个。

Input
第1行：1个整数T（1<=T<=50000)，表示有多少组测试数据。
第2 - T+1行：每行三个整数N，A,B（1<=N，A，B<=2147483647)
Output
对于每组测试数据输出一个数表示满足条件的集合的数量，占一行。
Input示例
2
5 2 4
10 2 3
Output示例
1
2
思路：
设A的倍数x，B的倍数y，则有Ax+By=N+1
利用exgcd，求Ax+By=gcd(A,B)的解，在求出符合题意最小的x
要注意x==0的情况是不符合题意的
判断第一组解是否符合题意，不符合
然受剩余的部分除以lcm(A,B)即可得到
注：最后除以lcm的证明
证：当x为最小正整数的第一组解符合题意的时候有（设此时为x0，y0）：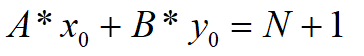

设增量为k,则有：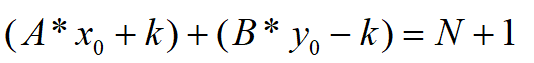

此时仍要满足以下等式：

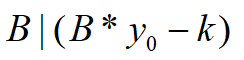
对于第一个式子，显然A*x0满足条件，即需要满足：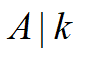

同理有：

所以k最小为lcm(A,B)

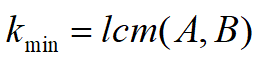
代码：

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
ll exgcd(ll a, ll b, ll &x, ll&y) {
    if(!b) {
        x=1;
        y=0;
        return a;
    }
    ll ans=exgcd(b,a%b,x,y);
    ll temp=x;
    x=y;
    y=temp-a/b*y;
    return ans;
}
int main() {
    ios::sync_with_stdio(false);
    ll T,N,A,B,x,y,sum;
    cin>>T;
    while(T--) {
        sum=0;
        cin>>N>>A>>B;
        ll g=exgcd(A,B,x,y);
        if((N+1)%g!=0) {
            cout<<"0"<<endl;
            continue;
        }
        x=(N+1)/g*x;
        ll b2=B/g;
        x=(x%b2+b2)%b2;
        if(!x) x=b2;
        y=(N+1-x*A)/B;
        if(x>=1&&x*A<=N&&y>=1&&y*B<=N&&((x*A+y*B)==(N+1)))
            sum++;
        else {
            cout<<"0"<<endl;
            continue;
        }
        ll lcm;
        if(!A/g) lcm=A/g*B;
        else lcm=B/g*A; 
        ll t=(N-x*A)/lcm;
        if(t>0) sum+=t;
        cout<<sum<<endl;
    } 
    return 0;
}