Wannafly模拟赛5 A Split 暴力 二分加速

你有一个大小为𝑆的𝐽𝑎𝑏𝑏𝑦，每次你可以从你已有的𝐽𝑎𝑏𝑏𝑦中选择一个大小不为1的𝐽𝑎𝑏𝑏𝑦，设他的大小为𝑄，然后把它分裂成𝑎和𝑄−𝑎，其中1≤𝑎<𝑄，这样你获得的收益是𝑎∗(𝑄−𝑎)给定𝑆，𝑀，求最少分裂几次才能得到至少𝑀的收益

思路：

首先需要证明

假设已经将题目中的S分成了n等份，那么对于当前分裂方式能够取得的最大收益需要满足：

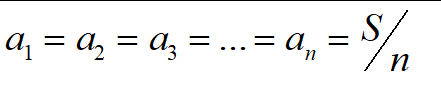当前假设S/n余数为0，或者尽可能接近均分

举例：

eg1. S=10 M=33

第一种方式：

所能够获得总收益为 come=5*5+2*3=31<33,若再将另外一个5分解才能满足>=33，此时分裂次数为3次

第二种方式：

此时总收益为 come=4*6+3*3=33 符合要求，分裂次数为2

对于第一种方式 （5,5）对于10是最优解，（2,3）对于5是最优解，但（2,3,5）对于10不是最优解

对于第二种方式（3,3）对于6是最优解，（4,6）对于10是最优解（再无法均分的情况下），同时（3,43,4）对于10是最优解，均分方式

eg2.假设最后分成了4份，如下：

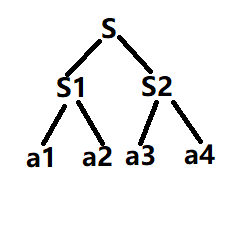
则有：

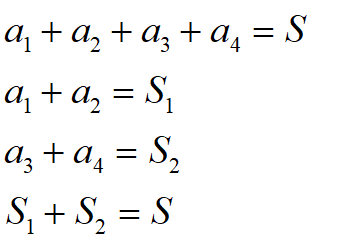
总收益为：

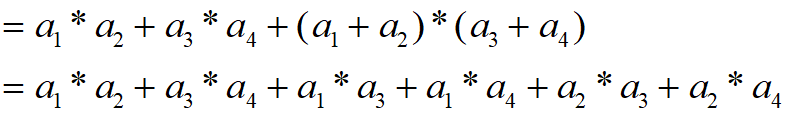
则需保证(a_1,a₂)对于S₁最优，(a_3,a₄)对于S₂最优

那么(a_1,a₃)，(a_1,a₄)，(a_2,a₃)，(a_2,a₄)也要保证最优，必有a₁=a₂=a₃=a₄=S/4（尽量平均分）

推论：对于总收益总能够表示为

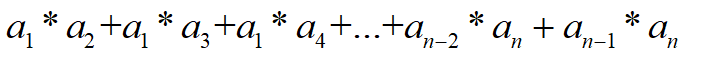
发现　　a₁与其余每一项都有乘积形式

　　　　a₂与其余每一项都有乘积形式

　　　　...

　　　　a_n与其余每一项都有乘积形式

这就要求尽可能将S均分给a_i

解题思路：

枚举能够分成的份数从2到S，计算当前份数下能够获取的最大收益值与M比较，大于等于就跳出

暴力代码：

#include <bits/stdc++.h>
using namespace std;
int main() {
    int s,m;
    scanf("%d %d",&s,&m);
    for(int i=2;i<=s;++i) {
        long long come=0;//总收益
        long long sum=0;//由下往上的数字和
        int ai=s/i;
        int r=s%i;
        if(r>=2) {
            come=(ai+1)*(ai+1);
            sum=(ai+1)*2;
        } else if(r==1) {
            come=(ai+1)*ai;
            sum=ai*2+1;
        } else {
            come=ai*ai;
            sum=ai*2;
        }
        int num;
        for(int j=3;j<=i;++j) {
            if(j<=r) num=ai+1;
            else num=ai;
            come+=num*sum;
            sum+=num;
        }
        if(come>=m) {
            printf("%d\n",i-1);
            return 0;
        }
    }
    printf("-1\n");
    return 0;
}

二分加速代码：二分分割次数，速度更快

#include <bits/stdc++.h>
using namespace std; 
long long  check(int s,int k)
{
    k++;//分割成k++份
    int  num=s/k;//每份的大小
    int  r=s%k;//多出来的部分
    long long ans=0;//当前划分最大收益
    for(int i=1;i<=r;++i){
        ans+=(num+1)*(s-num-1);
        s-=num+1;
    }
    for(int i=r+1;i<k;++i)
    {
        ans+=num*(s-num);
        s-=num;
    }
    return ans;
}
 
int main(){
    int  s,m;
    scanf("%d %d",&s,&m);
    int l=1,r=s-1;
    int k=-1;
    while(l<=r){
        int mid=(l+r)>>1;
        if(check(s,mid)>=m){
            r=mid-1;
            k=mid;
        }else l=mid+1;
    }
    printf("%d\n",k);
    return 0;
}