HDU 5194 DZY Loves Balls
DZY Loves Balls
Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 65536/65536 K (Java/Others)Total Submission(s): 807 Accepted Submission(s): 439
Problem Description
There are n black
balls and m white
balls in the big box.
Now, DZY starts to randomly pick out the balls one by one. It forms a sequenceS .
If at the i -th
operation, DZY takes out the black ball, Si=1 ,
otherwise Si=0 .
DZY wants to know the expected times that '01' occurs inS .
Now, DZY starts to randomly pick out the balls one by one. It forms a sequence
DZY wants to know the expected times that '01' occurs in
Input
The input consists several test cases. (TestCase≤150 )
The first line contains two integers,n , m(1≤n,m≤12)
The first line contains two integers,
Output
For each case, output the corresponding result, the format is p/q (p and q are
coprime)
Sample Input
1 1 2 3
Sample Output
1/2 6/5HintCase 1: S='01' or S='10', so the expected times = 1/2 = 1/2 Case 2: S='00011' or S='00101' or S='00110' or S='01001' or S='01010' or S='01100' or S='10001' or S='10010' or S='10100' or S='11000', so the expected times = (1+2+1+2+2+1+1+1+1+0)/10 = 12/10 = 6/5
题目大意:
给你n个黑球,m个白球,黑球标记为1,白球标记为0,问在所有的组合当中一共出现了多少个“01”串。
解题思路:
用概率统计的角度讲,这就是一个n重的伯努利试验。首先,确定一个随机变量。
设置为Xi,则在Xi位置上出现白球,并在X(i+1)位置上出现黑球的概率是p=(m/(n+m))*(n/(n+m-1))。这就是出现01串的概率,否则其他的情况概记为q=1-p。
即Xi只有两种状态,出现01串为1,否则为0。如下图所示。
这就是一个最为简单的二项分布了,以为Xi的取值是从1-(m+n-1)的。
所以有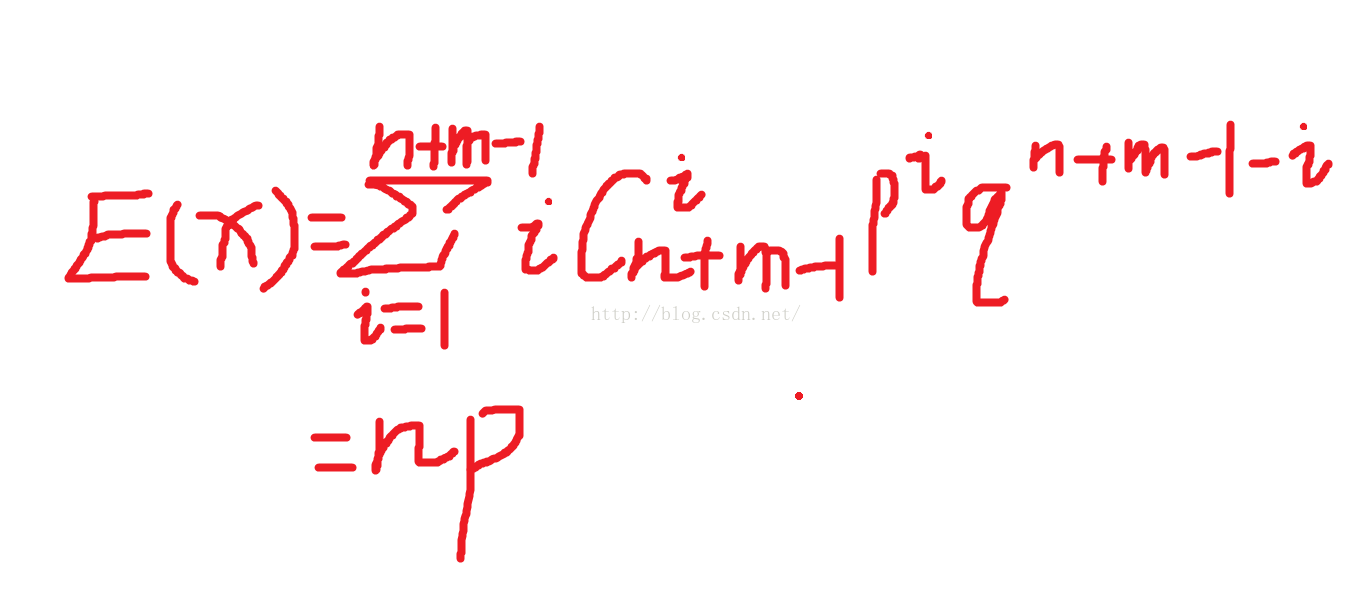
得E(X)=(m/(m+n))*(n/(n+m-1))*(n+m-1)=(m*n)/(m+n)。
程序里面需要求的就是m*n和m+n的最大公约数化简了。
源代码:
#include<iostream>
#include<stdio.h>
#include<stdlib.h>
#include<string>
#include<string.h>
#include<math.h>
#include<map>
#include<vector>
#include<algorithm>
#include<queue>
using namespace std;
#define MAX 0x3f3f3f3f
#define MIN -0x3f3f3f3f
#define PI 3.14159265358979323
#define N 1005
int gcd(int n, int m)
{
int temp;
if (m > n)
swap(m, n);
if (m == 1 || n == 1)
return 1;
temp = n%m;
while (temp != 0)
{
n = m;
m = temp;
temp = n%m;
}
return m;
}
int main()
{
int n, m;
int num;
int nn, mm;
while (scanf("%d%d", &n, &m) != EOF)
{
nn = m*n;
mm = m + n;
num = gcd(nn, mm);
printf("%d/%d\n", nn / num, mm / num);
}
return 0;
}

