A Path Plan（2018黑龙江省赛）

又get 新知识   Lindström–Gessel–Viennot引理

改引理主要是解决n条严格不相交的路径的问题

其中ai代表路径的起点,  bi代表路径的终点,  e(ai,bj)代表ai到bj的方案数，答案是这个行列式的值 

 

对于这道题而言，知道这个引理，这就是水题啊

 

其他知识：求组合数，本文采用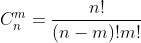这个公式，因为数据是2e5，所以提前将阶乘存起来，而阶乘的逆，先求出最后n!的逆(我采用的是费马小定理)，记为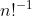，,所以 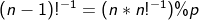,以此类推。

 

code:

#include <bits/stdc++.h>
 
using namespace std;
 
const int MOD = 1e9 + 7;
typedef long long ll;
const int N = 2e5 + 10;
 
ll f[N],finv[N];
ll fast_pow(ll a,ll n)
{
    ll ans = 1;
    while(n)
    {
        if(n&1) ans = (ans * a)%MOD;
        a = (a * a)%MOD;
        n >>= 1;
    }
    return ans;
}
ll C(ll n,ll m)
{
    return (n<0||m<0||n<m)?0:f[n]*(finv[m])%MOD*finv[n-m]%MOD;
}
void init()
{
    f[0]=1;
    for(int i=1;i< N;i++)
        f[i]=f[i-1]*i%MOD;
    finv[N-1] = fast_pow(f[N-1],MOD-2);
    for (int i=N-1; i > 0; i--)
        finv[i-1]=finv[i]*i%MOD;
}
 
int main()
{
    int t;
    init();
    scanf("%d",&t);
    while(t--)
    {
        int a,b,c,d;
        scanf("%d%d%d%d",&a,&b,&c,&d);
        ll ans = (C(a+c,a)*C(b+d,b) % MOD - C(b+c,b)*C(a+d,a) % MOD + MOD)%MOD;
        printf("%lld\n",ans);
    }
    return 0;
}