hdu 6395 Sequence

Sequence

Problem Description

Let us define a sequence as below

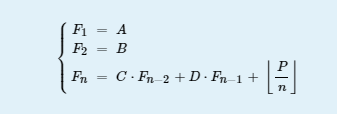
  Your job is simple, for each task, you should output Fn module 1e9+7.

 

Input

The first line has only one integer T, indicates the number of tasks.

Then, for the next T lines, each line consists of 6 integers, A , B, C, D, P, n.

1≤T≤200≤A,B,C,D≤1e9 1≤P,n≤1e9

 

Sample Input

2 3 3 2 1 3 5 3 2 2 2 1 4

 

Sample Output

36 24

 

 

Source

2018 Multi-University Training Contest 7

 

好菜呀。。。。

很明显是一道矩阵快速幂的题，但就是不知道怎么推.

对于 p/i 这个数 肯定是 p 的因子，因此不会超过2 * sqrt(p) 个，因此根据这个来分块，时间复杂度是2 * sqrt(p) * log(n) 

 

AC code:

#include <bits/stdc++.h>

using namespace std;
const int MOD = 1e9 + 7;
typedef long long LL;
const int M = 3;
struct Matrix{
    LL matrix[M][M];
};
void init(Matrix &res){
    for(int i=0;i<M;i++)
    {
        for(int j=0;j<M;j++)
            res.matrix[i][j]=0;
        res.matrix[i][i]=1;
    }
}
Matrix multiplicative(Matrix a,Matrix b){
    Matrix res;
    memset(res.matrix,0,sizeof(res.matrix));
    for(int i = 0 ; i < M ; i++)
        for(int j = 0 ; j < M ; j++)
            for(int k = 0 ; k < M ; k++)
                res.matrix[i][j] =(res.matrix[i][j]%MOD+a.matrix[i][k]%MOD*b.matrix[k][j]%MOD)%MOD;
return res;
}
Matrix pow(Matrix mx,int m){
    Matrix res,base=mx;
    init(res); //初始为单位矩阵，即除主对角线都是1外，其他都是0
    while(m)
    {
        if(m&1)
            res=multiplicative(res,base);
        base=multiplicative(base,base);
        m>>=1;
    }
    return res;
}

int main()
{
    int t;
    LL a,b,c,d,n,p;
    a = 3;b = 4;c = 5;d = 6;
    scanf("%d",&t);
    while(t--)
    {
        scanf("%lld%lld%lld%lld%lld%lld",&a,&b,&c,&d,&p,&n);
        if(n == 1)  printf("%lld\n",a);
        else if(n == 2) printf("%lld\n",b);
        else{
            int st = 3,ed;
            LL A,B;
            while(st <= n)
            {
                if(p/st == 0)   ed = n;
                else ed = min(n,p/(p/st));
                Matrix base = {
                        d,c,1,
                        1,0,0,
                        0,0,1,
                };
                Matrix pw = pow(base,ed - st + 1);
                B = (b * pw.matrix[0][0] % MOD + a * pw.matrix[0][1] + 1LL * (p/st) * pw.matrix[0][2] % MOD) % MOD;
                A = (b * pw.matrix[1][0] % MOD + a * pw.matrix[1][1] + 1LL * (p/st) * pw.matrix[1][2] % MOD) % MOD;
                b = B; a = A;
                st = ed + 1;
            }
            printf("%lld\n",b);
        }
    }
    return 0;
}