阅读《计算机图形学编程（使用OpenGL和C++）》12 - 光照

现在最常见的光照模型称为“ADS”模型，因为它们基于标记为A、D和S的3种类型的反射。

●环境光反射（Ambient reflection）模拟低级光照，影响场景中的所有物体。

●漫反射（Diffuse reflection）根据光线的入射角度调整物体亮度。

●镜面反射（Specular reflection）用以展示物体的光泽，通过在物体表面上，光线最直接地反射到我们的眼睛的位置，策略性地放置适当大小的高光来实现。

ADS模型可用于模拟不同的光照效果和各种材质。

场景的绘制最终是由片段着色器为屏幕上的每个像素输出颜色而实现的。使用ADS光照模型需要指定由于像素的RGBA输出值上的光照而产生的分量。因素包括：

●光源类型及其环境、漫反射和镜面反射特性；

●对象材质的环境、漫反射和镜面反射特征；

●对象的材质指定为“光泽”；

●光线照射物体的角度；

●从中查看场景的角度。

光源有许多类型，每种光源具有不同的特性，需要不同的步骤来模拟其效果。常见光源类型有：

全局环境光是最简单的光源模型。它没有光源位置——无论场景中的对象在何处，其上的每个像素都有着相同的光照。仅具有环境光反射分量，用RGBA值设定；它没有漫反射或镜面反射分量。例如，全局环境光可以定义如下：

float globalAmbient[4] = { 0.7f, 0.7f, 0.7f, 1.0f };

RGBA的取值范围为0～1，全局环境光通常被建模为偏暗的白光，其中RGB各值设为0～1的相同的小数，alpha设置为1。

定向光或远距离光也没有源位置，但它具有方向。它可以用来模拟光源距离非常远，以至于光线接近平行的情况，例如阳光。建模定向光需要指定其方向（以向量形式）及其环境、漫反射和镜面特征（以RGBA值）。指向Z轴负方向的红色定向光可以指定如下：

float lightAmbient[4] = { 0.1f, 0.0f, 0.0f, 1.0f };
float lightDiffuse[4] = { 1.0f, 0.0f, 0.0f, 1.0f };
float lightSpecular[4] = { 1.0f, 0.0f, 0.0f, 1.0f };
float lightSpecular[3] = { 0.0f, 0.0f, -1.0f};

位置光在3D场景中具有特定位置。靠近场景的光源，例如台灯，蜡烛等。位置光还可以包含衰减因子，以模拟它们的强度随距离减小的程度。与我们看到的其他类型的光源一样，位置光具有指定为RGBA值的环境光反射、漫反射和镜面反射特性。位置（5,2,−3）处的红色位置光可以指定如下例：

float lightAmbient[4] = { 0.1f, 0.0f, 0.0f, 1.0f };
float lightDiffuse[4] = { 1.0f, 0.0f, 0.0f, 1.0f };
float lightSpecular[4] = { 1.0f, 0.0f, 0.0f, 1.0f };
float lightSpecular[3] = { 5.0f, 2.0f, -3.0f};

衰减因子有多种建模方式。其中一种方式是使用恒定、线性和二次方（分别称为kc, kl和kq）衰减，并引入非负可调参数。这些参数与离光源的距离（d）结合进行计算：

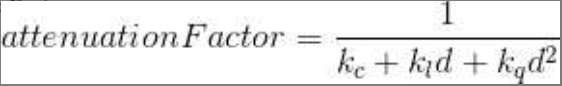
将这个因子与光的强度相乘可以使距光更远时，光的强度衰减更多。注意，kc应当永远设置为大于等于1的值，从而使得衰减因子落入[0…1]区间，并当d增大时接近于0。

聚光灯（spotlight）同时具有位置和方向。其“锥形”效果可以使用0°～90°的截光角θ来模拟，指定光束的半宽度，并使用衰减指数来模拟随光束角度的强度变化。如图所示，我们确定聚光灯方向与从聚光灯到像素的向量之间的角度φ。当φ小于θ时，我们通过将φ的余弦提高到衰减指数来计算强度因子（当φ大于θ时，强度因子设置为0）。结果是强度因子的范围为0～1。衰减指数会影响当角度φ增加时，强度因子趋于0的速率。然后将强度因子乘以光的强度以模拟锥形效果。

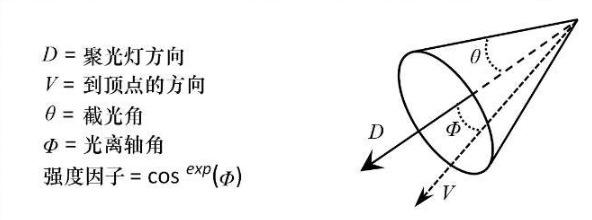
通过指定4个值（我们已经熟悉其中3个值——环境光、漫反射和镜面RGB颜色），可以在ADS光照模型中模拟材质。第四种叫作光泽，它被用来为所选材质建立一个合适的镜面高光。 

透明度由RGBA标准中的第四个（alpha）通道的不透明度来实现。取值为1.0是表示完全不透明，取值为0时表示完全透明。

预定义一些可供选择的材质，在使用时会很方便。因此我们需要在Utils.cpp文件中添加如下代码：

 1 // 黄金材质 — 环境光、漫反射、镜面反射和光泽
 2 float * Utils::goldAmbient()
 3 {
 4     static float a[4] = { 0.2473f, 0.1995f, 0.0745f, 1 };
 5     return (float*)a;
 6 }
 7 
 8 float * Utils::goldDiffuse()
 9 {
10     static float a[4] = { 0.7516f, 0.6065f, 0.2265f, 1 };
11     return (float*)a;
12 }
13 
14 float * Utils::goldSpecular()
15 {
16     static float a[4] = { 0.6283f, 0.5559f, 0.3661f, 1 };
17     return (float*)a;
18 }
19 
20 float Utils::goldShininess()
21 {
22     return 51.2f;
23 }
24 // 白银材质 — 环境光、漫反射、镜面反射和光泽
25 float * Utils::silverAmbient()
26 {
27     static float a[4] = { 0.1923f, 0.1923f, 0.1923f, 1 };
28     return (float*)a;
29 }
30 
31 float * Utils::silverDiffuse()
32 {
33     static float a[4] = { 0.5075f, 0.5075f, 0.5075f, 1 };
34     return (float*)a;
35 }
36 
37 float * Utils::silverSpecular()
38 {
39     static float a[4] = { 0.5083f, 0.5083f, 0.5083f, 1 };
40     return (float*)a;
41 }
42 
43 float Utils::silverShininess()
44 {
45     return 51.2f;
46 }
47 // 青铜材质 — 环境光、漫反射、镜面反射和光泽
48 float * Utils::bronzeAmbient()
49 {
50     static float a[4] = { 0.2125f, 0.1275f, 0.0540f, 1 };
51     return (float*)a;
52 }
53 
54 float * Utils::bronzeDiffuse()
55 {
56     static float a[4] = { 0.7140f, 0.4284f, 0.1814f, 1 };
57     return (float*)a;
58 }
59 
60 float * Utils::bronzeSpecular()
61 {
62     static float a[4] = { 0.3936f, 0.2719f, 0.1667f, 1 };
63     return (float*)a;
64 }
65 
66 float Utils::bronzeShininess()
67 {
68     return 25.6f;
69 }

 我们需要做的基础ADS光照计算是确定每个像素的反射强度（Reflection Intensity，I）。我们需要计算每个光源对于每个像素的环境光反射、漫反射和镜面反射分量，并求和。计算过程如下：

Iobserved = Iambient + Idiffuse + Ispecular

这些计算都基于场景内的光源类型以及渲染中模型的材质类型。

环境光分量是最简单的。它的值是场景环境光与材质环境光分量的乘积：

Iambient = Lightambient * Materialambient

光与材质亮度都是RGB值，计算可以更准确地描述为：

　　Iredambient = Lightredambient * Materialredambient

　　Igreenambient = Lightgreenambient * Materialgreenambient

　　Iblueambient = Lightblueambient * Materialblueambient

下面同理。

漫反射分量基于光对于平面的入射角。朗伯余弦定律（1760年出版）确定了表面反射的光量与光入射角的余弦成正比。可以建模为如下公式：

Idiffuse = Lightdiffuse * Materialdiffuse * cos(θ)

 确定入射角θ需要

（a）求解从所绘制向量到光源的向量（或者与光照方向相反的向量）

（b）求解所渲染物体表面的法（垂直）向量。让我们将其分别称为L和N

 

 

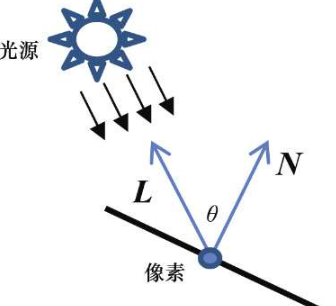
 在5数学部分，cos(θ)可以通过点乘计算得出。漫反射分量仅当表面暴露在光照中时起作用，即当−90 < θ < 90，cos(θ) > 0时。

Idiffuse = Lightdiffuse * Materialdiffuse * 

 

 镜面反射分量决定所渲染的像素是否需要作为“镜面高光”的一部分变亮。它不止与光源的入射角相关，也与光在表面上的反射角以及观察点与反光表面之间的夹角相关。

R代表光反射的方向，V（叫作观察向量view vector）是从像素到眼睛的向量。注意，V是对从眼睛到像素的向量取反（在相机空间中，眼睛位于原点）。在R与V之间的小夹角φ越小，眼睛越靠近光轴，或者说看向反射光，因此像素的镜面高光分量也就越大（像素看来应该更亮）。

 

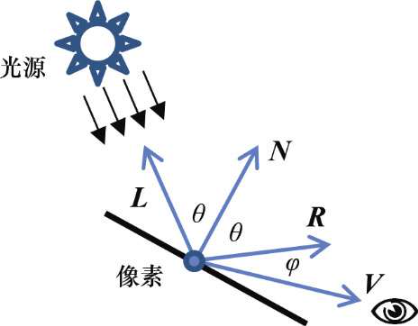
 φ用于计算镜面反射分量的方式取决于所渲染物体的“光泽度”。极端闪亮的物体，如镜子，其镜面高光非常小——它们将入射的光直接反射给了眼睛。不那么闪亮的物体，其镜面高光会扩散开来，因此高光会包含更多的像素。

反光度通常用衰减函数来建模，这个衰减函数用来表达随着角度φ的增大，镜面反射分量降低到0的速度。我们可以用cos(φ)来对衰减进行建模，通过余弦函数的乘方来增减反光度，如cos(φ), cos2(φ), cos3(φ), cos10(φ), cos50(φ)等，

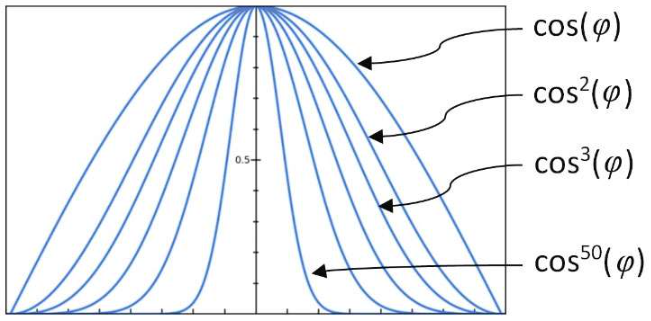
注意，指数中的阶数越高，衰减越快，因此在视角光轴外的反光像素镜面反射分量越小。我们将衰减函数cosn(φ)中的指数n叫作材质的反光度因子。现在我们可以给出完整的镜面反射计算： 

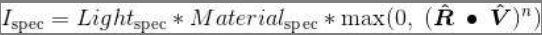
 与之前计算漫反射一样，我们使用了max()函数。在本例中，我们需要确保镜面反射分量不使用cos(φ)所产生的负值，如果使用了负值，则会有奇怪的伪影，如“暗”镜面高光。

Gouraud着色（双线性光强插值法）

Gouraud着色过程如下。

（1）确定每个顶点的颜色，以及光照相关计算。

（2）允许正常的光栅化过程在插入像素时对颜色也进行插值（同时也对光照进行插值）。

 

  1 ...
  2 #include "Torus.h"
  3 #include "Utils.h"
  4 ...
  5 // 给display()用
  6 GLuint mvLoc, projLoc, nLoc;
  7 int width, height;
  8 float aspect;
  9 glm::mat4 pMat, vMat, mMat, mvMat, invTrMat;
 10 glm::mat4 tMat, rMat;
 11 GLuint vLoc, tfLoc, mLoc;
 12 stack<glm::mat4> mvStack;
 13 // 着色器统一变量中的位置
 14 GLuint globalAmbLoc, ambLoc, diffLoc, specLoc, posLoc, mAmbLoc, mDiffLoc, mSpecLoc, mShiLoc;
 15 glm::vec3 currentLightPos, lightPosV; //在模型和视觉空间中的光照位置， Vector3f类型
 16 float lightPos[3]; // 光照位置的浮点数组
 17 // 初始化光照位置
 18 glm::vec3 initialLightLoc = glm::vec3(5.0f, 2.0f, 2.0f);
 19 // 白光特性
 20 float globalAmbient[4] = { 0.7f, 0.7f, 0.7f, 1.0f };
 21 float lightAmbient[4] = { 0.0f, 0.0f, 0.0f, 1.0f };
 22 float lightDiffuse[4] = { 1.0f, 1.0f, 1.0f, 1.0f };
 23 float lightSpecular[4] = { 1.0f, 1.0f, 1.0f, 1.0f };
 24 // 黄金材质特性
 25 float* matAmb = Utils::goldAmbient();
 26 float* matDif = Utils::goldDiffuse();
 27 float* matSpe = Utils::goldSpecular();
 28 float matShi = Utils::goldShininess();
 29 Torus myTorus(0.5f, 0.2f, 48);
 30 ...
 31 void installLights(glm::mat4 vMatrix)
 32 {
 33     //将光源位置转换为视图空间坐标，并存入浮点数组
 34     lightPosV = glm::vec3(vMatrix * glm::vec4(currentLightPos, 1.0));
 35     lightPos[0] = lightPosV.x;
 36     lightPos[1] = lightPosV.y;
 37     lightPos[2] = lightPosV.z;
 38     //在着色器中获取光源位置和材质属性
 39     globalAmbLoc = glGetUniformLocation(renderingProgram, "globalAmbient");
 40     ambLoc = glGetUniformLocation(renderingProgram, "light.ambient");
 41     diffLoc = glGetUniformLocation(renderingProgram, "light.diffuse");
 42     specLoc = glGetUniformLocation(renderingProgram, "light.specular");
 43     posLoc = glGetUniformLocation(renderingProgram, "light.position");
 44     mAmbLoc = glGetUniformLocation(renderingProgram, "material.ambient");
 45     mDiffLoc = glGetUniformLocation(renderingProgram, "material.diffuse");
 46     mSpecLoc = glGetUniformLocation(renderingProgram, "material.specular");
 47     mShiLoc = glGetUniformLocation(renderingProgram, "material.shininess");
 48     //在着色器中为光源与材质统一变量赋值
 49     glProgramUniform4fv(renderingProgram, globalAmbLoc, 1, globalAmbient);
 50     glProgramUniform4fv(renderingProgram, ambLoc, 1, lightAmbient);
 51     glProgramUniform4fv(renderingProgram, diffLoc, 1, lightDiffuse);
 52     glProgramUniform4fv(renderingProgram, specLoc, 1, lightSpecular);
 53     glProgramUniform3fv(renderingProgram, posLoc, 1, lightPos);
 54     glProgramUniform4fv(renderingProgram, mAmbLoc, 1, matAmb);
 55     glProgramUniform4fv(renderingProgram, mDiffLoc, 1, matDif);
 56     glProgramUniform4fv(renderingProgram, mSpecLoc, 1, matSpe);
 57     glProgramUniform1f(renderingProgram, mShiLoc, matShi);
 58 }
 59 
 60 void setupVertices(void)
 61 {    
 62     //顶点同前面环形
 63 }
 64 ...
 65 void display(GLFWwindow* window, double currentTime)
 66 {
 67     ...
 68     // 用于模型-视图变换、投影以及逆转置（法向量）矩阵的统一变量
 69     mvLoc = glGetUniformLocation(renderingProgram, "mv_matrix");
 70     projLoc = glGetUniformLocation(renderingProgram, "proj_matrix");
 71     nLoc = glGetUniformLocation(renderingProgram, "norm_matrix");    
 72     // 模型-视图变换同前面旋转的太阳
 73     ...
 74     // 基于当前光源位置，初始化光照
 75     currentLightPos = glm::vec3(initialLightLoc.x, initialLightLoc.y, initialLightLoc.z);
 76     installLights(vMat);
 77 
 78     // 构建MV矩阵的逆转置矩阵，以变换法向量
 79     invTrMat = glm::transpose(glm::inverse(mvStack.top()));//mvMat
 80 
 81     // 太阳旋转
 82     glUniformMatrix4fv(mvLoc, 1, GL_FALSE, glm::value_ptr(mvStack.top())); //mvMat
 83     glUniformMatrix4fv(nLoc, 1, GL_FALSE, glm::value_ptr(invTrMat));
 84 
 85     glBindBuffer(GL_ARRAY_BUFFER, vbo[0]);
 86     glVertexAttribPointer(0, 3, GL_FLOAT, GL_FALSE, 0, 0);
 87     glEnableVertexAttribArray(0);
 88 
 89     glBindBuffer(GL_ARRAY_BUFFER, vbo[2]);
 90     glVertexAttribPointer(1, 3, GL_FLOAT, GL_FALSE, 0, 0);
 91     glEnableVertexAttribArray(1);
 92 
 93     glEnable(GL_CULL_FACE); // 要求识别并“剔除”背向的三角形
 94     glFrontFace(GL_CCW);
 95     glEnable(GL_DEPTH_TEST);
 96     glDepthFunc(GL_LEQUAL);
 97 
 98     glBindBuffer(GL_ELEMENT_ARRAY_BUFFER, vbo[3]);
 99     glDrawElements(GL_TRIANGLES, myTorus.getNumIndices(), GL_UNSIGNED_INT, 0);
100 }

顶点着色器

 1 #version 460
 2 layout (location = 0) in vec3 vertPos;
 3 layout (location = 1) in vec3 vertNormal;
 4 out vec4 varyingColor;
 5 
 6 struct PositionalLight
 7 {
 8 vec4 ambient;
 9 vec4 diffuse;
10 vec4 specular;
11 vec3 position;
12 };
13 
14 struct Material
15 {
16 vec4 ambient;
17 vec4 diffuse;
18 vec4 specular;
19 float shininess;
20 };
21 
22 uniform mat4 norm_matrix;  // 用来变换法向量
23 uniform mat4 mv_matrix;
24 uniform mat4 proj_matrix;
25 uniform Material material; 
26 uniform vec4 globalAmbient;
27 uniform PositionalLight light;
28 
29 void main(void)
30 { 
31     vec4 color;
32     // 将顶点位置转换到视觉空间
33     // 将法向量转换到视觉空间
34     // 计算视觉空间光照向量（从顶点到光源）
35     vec4 P = mv_matrix * vec4(vertPos, 1.0);
36     vec3 N = normalize((norm_matrix * vec4(vertNormal, 1.0)).xyz);
37     vec3 L = normalize(light.position - P.xyz);
38     // 视觉向量等于视觉空间中的负顶点位置
39     vec3 V = normalize(-P.xyz);
40     // R是-L的相对于表面向量N的镜像
41     vec3 R = reflect(-L, N);
42     // 环境光、漫反射和镜面反射分量
43     vec3 ambient = ((globalAmbient * material.ambient) + (light.ambient * material.ambient)).xyz;
44     vec3 diffuse = light.diffuse.xyz * material.diffuse.xyz * max(dot(N, L), 0.0);
45     vec3 specular = material.specular.xyz * light.specular.xyz * pow(max(dot(R, V), 0.0f), material.shininess);
46     // 将颜色输出发送到片段着色器
47     varyingColor = vec4((ambient + diffuse + specular), 1.0);
48     // 将位置发送到片段着色器，如前
49     gl_Position = proj_matrix * mv_matrix * vec4(vertPos, 1.0);
50 }

片段着色器

 1 #version 460
 2 out vec4 fragColor;
 3 in vec4 varyingColor;
 4 
 5 // 与顶点着色器相同的统一变量
 6 // 但并不直接在当前片段着色器使用
 7 
 8 struct PositionalLight
 9 {
10 vec4 ambient;
11 vec4 diffuse;
12 vec4 specular;
13 vec3 position;
14 };
15 
16 struct Material
17 {
18 vec4 ambient;
19 vec4 diffuse;
20 vec4 specular;
21 float shininess;
22 };
23 
24 uniform mat4 norm_matrix;  // 用来变换法向量
25 uniform mat4 mv_matrix;
26 uniform mat4 proj_matrix;
27 uniform Material material; 
28 uniform vec4 globalAmbient;
29 uniform PositionalLight light;
30 
31 void main(void)
32 { 
33 //color = vec4(1.0, 0.0, 0.0, 1.0);
34 fragColor = varyingColor;
35 }

效果如下所示：

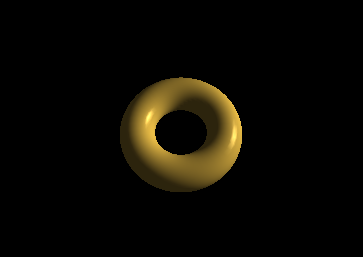
 installLights()，将光源在视觉空间中的位置，以及材质的ADS特性，读入相应的统一变量以供着色器使用。

其中一个重要的细节是变换矩阵MV，用来将顶点位置移动到视觉空间，是MV的逆转置矩阵，这个新增的矩阵叫作“invTrMat”，通过统一变量传入着色器。

顶点着色器代码中有我们第一次使用了结构体语法的示例。GLSL“结构体”就像一个数据类型，它有名称和一组字段。要注意字段选择器符号“.xyz”，这是将vec4转换为仅包含其前3个元素的等效vec3的快捷方式。

绝大多数光照计算发生在顶点着色器中。对于每个顶点，将适当的矩阵变换应用于顶点位置和相关的法向量，并计算用于光方向（L）和反射（R）的向量。然后执行ADS计算，得到每个顶点的颜色（代码中名为varyingColor）。颜色作为正常光栅化过程的一部分进行插值。之后片段着色器仅作为简单传递。冗长的统一变量声明列表也在片段着色器中，但实际上并没有在那里使用它们。

GLSL函数normalize()，它用来将向量转换为单位长度。正确地进行点积运算必须要先使用该函数。

reflect()函数则计算一个向量基于另一个向量的反射。

输出的环面中有很明显的伪影。其镜面高光有着块状、面片感。这种伪影在物体移动时会更加明显。

Gouraud着色也容易受到其他伪影影响。如果镜面高光整个范围都在模型中的一个三角形内——即高光范围内一个模型顶点也没有——那么它可能不会被渲染出来。由于镜面反射分量是依顶点计算的，因此，当模型所有顶点都没有镜面反射分量时，其光栅化后的像素也不会有镜面反射光。

Phong着色

Bui Tuong Phong在犹他大学的研究生期间开发了一种平滑的着色算法。该算法的结构类似于Gouraud着色的算法，其不同之处在于光照计算是按像素而非顶点完成。

之前部分在顶点着色器中完成的过程现在回放入片段着色器中进行。法向量插值的效果如图所示：

 

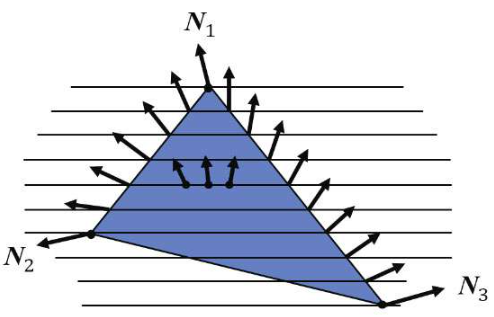
由于C++/OpenGL代码完全没有改变，在此我们只展示修改过的顶点着色器和片段着色器。 

顶点着色器

#version 460
layout (location = 0) in vec3 vertPos;
layout (location = 1) in vec3 vertNormal;
out vec3 varyingNormal; // 视觉空间顶点法向量
out vec3 varyingLightDir; // 指向光源的向量
out vec3 varyingVertPos; // 视觉空间中的顶点位置

struct PositionalLight
{
vec4 ambient;
vec4 diffuse;
vec4 specular;
vec3 position;
};

struct Material
{
vec4 ambient;
vec4 diffuse;
vec4 specular;
float shininess;
};

uniform mat4 norm_matrix;  // 用来变换法向量
uniform mat4 mv_matrix;
uniform mat4 proj_matrix;
uniform Material material; 
uniform vec4 globalAmbient;
uniform PositionalLight light;

void main(void)
{ 
    //输出顶点位置、光照方向和法向量到光栅器以进行插值
    varyingVertPos = (mv_matrix * vec4(vertPos, 1.0)).xyz;
    varyingLightDir = light.position - varyingVertPos; 
    varyingNormal = (norm_matrix * vec4(vertNormal, 1.0)).xyz; 
    
    gl_Position = proj_matrix * mv_matrix * vec4(vertPos, 1.0);
}

片段着色器

#version 460
out vec4 fragColor;
in vec3 varyingNormal; 
in vec3 varyingLightDir;
in vec3 varyingVertPos;

struct PositionalLight
{
vec4 ambient;
vec4 diffuse;
vec4 specular;
vec3 position;
};

struct Material
{
vec4 ambient;
vec4 diffuse;
vec4 specular;
float shininess;
};

uniform mat4 norm_matrix;  // 用来变换法向量
uniform mat4 mv_matrix;
uniform mat4 proj_matrix;
uniform Material material; 
uniform vec4 globalAmbient;
uniform PositionalLight light;

void main(void)
{ 
    // 正规化光照向量、法向量、视觉向量
    vec3 L = normalize(varyingLightDir);
    vec3 N = normalize(varyingNormal);
    vec3 V = normalize(-varyingVertPos);
    // 计算光照向量基于N的反射向量
    vec3 R = normalize(reflect(-L, N));
    // 计算光照与平面法向量间的角度
    float cosTheta = dot(L, N);
    // 计算视觉向量与反射光向量的角度
    float cosPhi = dot(V, R);
    // 计算ADS分量（按像素），并合并以构建输出颜色
    vec3 ambient = ((globalAmbient * material.ambient) + (light.ambient * material.ambient)).xyz;
    vec3 diffuse = light.diffuse.xyz * material.diffuse.xyz * max(cosTheta, 0.0);
    vec3 specular = light.specular.xyz * material.specular.xyz * pow(max(cosPhi, 0.0), material.shininess);
    fragColor = vec4((ambient + diffuse + specular), 1.0);
}

效果如下

 

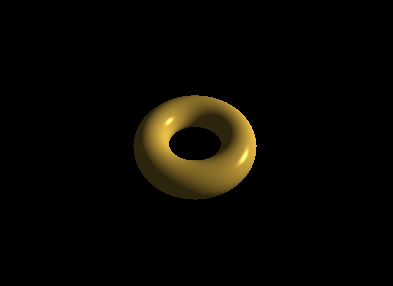
虽然Phong着色有着比Gouraud着色更真实的效果，但这是建立在增大性能消耗的基础上的。James Blinn在1977年提出了一种对于Phong着色的优化方法，被称为Blinn-Phong反射模型。这种优化是基于观察到Phong着色中消耗最大的计算之一是解出反射向量R。

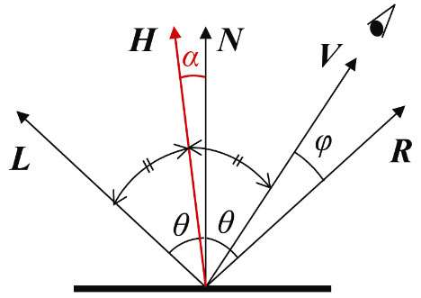
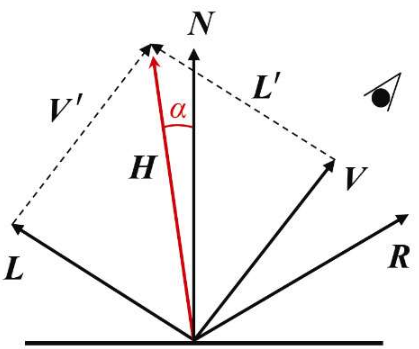
Blinn发现向量R在计算过程中并不是必需的——R只是用来计算角φ的手段。角φ的计算可以不用向量R，而通过L与V的角平分线向量H得到。如图所示，H和N之间的角α刚好等于1⁄2(φ)。

 

 角平分线向量可以简单地使用L+V得到，之后cos(α)可以通过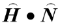的点积计算。

 

 这些计算可以在片段着色器中进行，甚至为了性能考虑（经过一些调整）也可以在顶点着色器中进行。

 同样C++/OpenGL代码完全没有改变。

顶点着色器

...
// 角平分线向量H作为新增的输出
out vec3 varyingHalfVector;
 ...
void main(void)
{ 
    // 与之前的计算相同，增加了 L+V 的计算
    varyingHalfVector = (varyingLightDir + (-varyingVertPos)).xyz;
    // 其余代码没改动
}

片段着色器

 1 ...
 2 in vec3 varyingHalfVector;
 3 ...
 4 void main(void)
 5 { 
 6     // 现在不需要计算R
 7     vec3 L = normalize(varyingLightDir);
 8     vec3 N = normalize(varyingNormal);
 9     vec3 V = normalize(-varyingVertPos);
10     vec3 H = normalize(varyingHalfVector);    
11     // 计算光照与平面法向量间的角度
12     float cosTheta = dot(L, N);
13     // 计算法向量N与角平分线向量H之间的角度
14     float cosPhi = dot(H, N);
15     // 角平分线向量H已经在顶点着色器中计算过，并在光栅器中进行过插值
16     vec3 ambient = ((globalAmbient * material.ambient) + (light.ambient * material.ambient)).xyz;
17     vec3 diffuse = light.diffuse.xyz * material.diffuse.xyz * max(cosTheta, 0.0);
18     vec3 specular = light.specular.xyz * material.specular.xyz * pow(max(cosPhi, 0.0), material.shininess*3.0);
19     // 最后乘以3.0作为改善镜面高光的微调
20     fragColor = vec4((ambient + diffuse + specular), 1.0);
21 }

效果如图所示：

初学光照看不太出来不同，我把三种效果放一起看看吧：

 

 

 眼睛花了

posted @ 2022-08-30 17:05  yangly  阅读(353)  评论(0)  编辑  收藏  举报