二叉树遍历理解

 

口诀：

前序遍历：根结点 ---> 左子树 ---> 右子树

中序遍历：左子树---> 根结点 ---> 右子树

后序遍历：左子树 ---> 右子树 ---> 根结点

层次遍历：仅仅需按层次遍历就可以

 

二叉树的遍历，是从左到右的，前、中、后这三个字代表着根结点的位置（其实也是最终根结点的位置）。

再次看到前序遍历，“前”就代表根结点在前，然后从左到右，就是：根结点——左子树——右子树

 

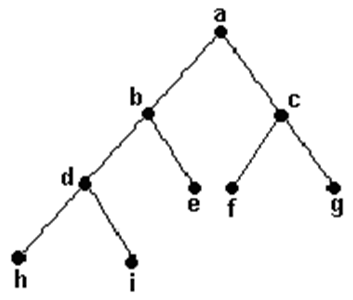
层次遍历就不详细讲解了，从上往下就ok了，结果是：abcdefghi

　　1、前序遍历思考方式：根——左——右。a，然后是左子树b，但是b也有左子树，此时把b再当成根，下一步应该是根b-左d-右e。到这，我们确定了a-b，由于d还有子树，到达d时，我们要重新统计根d-左h-右i，由于 h、i没有子树，这一步我们的顺序扩大到：a-b-d-h-i，d的子树已遍历，这时继续走根b-左d-右e，所以顺序后添加e，以此类推，补完整个结构，最后结果为：a-b-d-h-i-e-c-f-g。

　　2、中序遍历思考方式：左——根——右。此时起点是最左边的左子树h，左h-根d-右i，这个时候，我继续前序遍历的思考方式，得出的结果却是：h-d-b-a-i-e-f-c-g，而且中间逻辑有点诡异。这是为什么呢？急于获得答案，我先根据正确结果得结出一个规律：从上往下找，可以用前序的那种思维模式，每一步都是新起点，从下往上，是把它们这一部分作为一个整体，需要走完，才能往上找，如：d、h、i看成一个d点，d内的顺序（中序）是h-d-i，这时再把d当作左子树，继续遍历。按照规律，h-d-i（d点的内部顺序），d-b-e（b点的内部顺序），最后找出的顺序：h-d-i-b-e-a-f-c-g。

　　3、后序遍历思考方式：后序遍历，又叫后根遍历。
　　遍历顺序：左子树 -> 右子树 -> 根；左——右——根。结合中序得出的规律，把h-i-d看作d点的内部顺序，最后查找结果为：h-i-d-e-b-f-g-c-a。

　　先遍历左子树，然后遍历右子树，最后访问根节点；同样，在遍历左右子树的时候同样要先遍历左子树，然后遍历右子树，最后访问根节点。前图后序遍历结果如下。

 

 

总规律：上到下，新起点。下到上，根为口。（这个口是接口，接口内的东西，自己有顺序，整个接口再和外面排序）