3D旋转

该公式的证明在3D Math Primer for Graphics and Game Development
chapter5 .
假设v绕向量N(当然经过原点)旋转θ度,得到v′
v′ = vR(N, θ). 求矩阵R
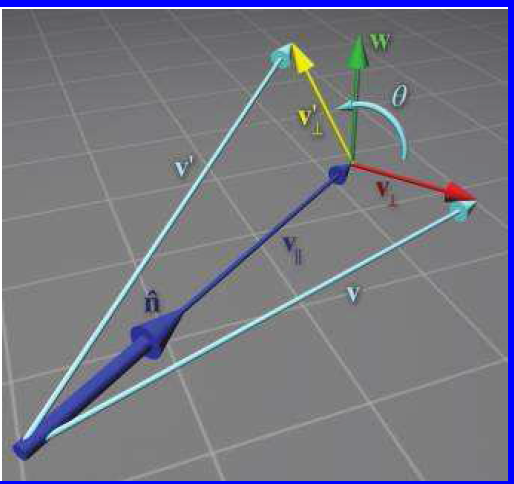
(注意:图示是左手坐标系,无论左右手坐标系,旋转角度总是逆时针方向为正,
N的方向是新的虚拟的Z轴方向,v1是X轴方向,)
把v分解成垂直和平行于N的v1(v垂直),v2(v平行)
同理v′分解成v1′和v2′
v2=v2′=(v·N)N
v1=v-v2
构造向量W,垂直于v1和v2,长度等于v1,
W=N×v1=N×v
这里把v1和W组成一个新的坐标系,v1是x轴,W是y轴,v1′是v1旋转θ之后得到。
v1′=cosθv1+ sinθW
=cosθ(v-(v·N)N)+ sinθ(N×v)
so,v'=v1'+v2=cosθ(v-(v·N)N)+ sinθ(N×v)+(v·N)N ...........................................................................式子3.0
=(1-cosθ)(v·N)N +cosθv+sinθ(N×v)
令e1=(1,0,0),e2=(0,1,0),e3=(0,0,1),采用OpenGL 矩阵,这里都是列形式。
R的三列自然就是[R(e1),R(e2),R(e3)]
N是(x,y,z),cosθ写为c,sinθ写为s,
对于e1,(v·N)N =(x^2,xy,xz),
sinθ(N×v)=(0,sz,-sy)
R(e1)=(1-c)(xx,xy,xz)+(c,0,0)+(0,sz,-sy)=(1-c)x*x+c,(1-c)xy+sz,(1-c)xz-sy.....................column one
for e2,(v·N)N=(xy,yy,yz), sinθ(N×v)=(-sz,0,sx)
R(e2)=(1-c)(xy,yy,yz)+(0,c,0)+(-sz,0,sx)=(1-c)xy-sz,(1-c)yy+c,(1-c)yz+sx...................column two
for e3,(v·N)N=(xz,yz,zz),sinθ(N×v)=(sy,-sx,0)
R(e3)=(1-c)(xz,yz,zz)+(0,0,c)+(sy,-sx,0)=(1-c)xz+sy,(1-c)yz-sx,(1-c)zz+c......................column three
四元数和旋转
平面复数的回顾
每一个 关于原点)的旋转都可以用一个复数
关于原点)的旋转都可以用一个复数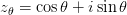 来表示。这是因为,对于每一个点
来表示。这是因为,对于每一个点
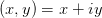 ,
,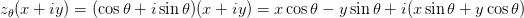
所以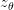 把
把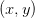 移到了
移到了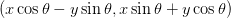 的位置,也就是旋转了
的位置,也就是旋转了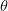
我们还可以把这个过程写成矩阵形式:
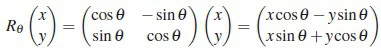
先介绍四元数的性质
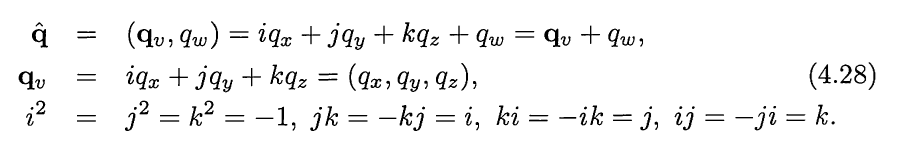
四元数相乘
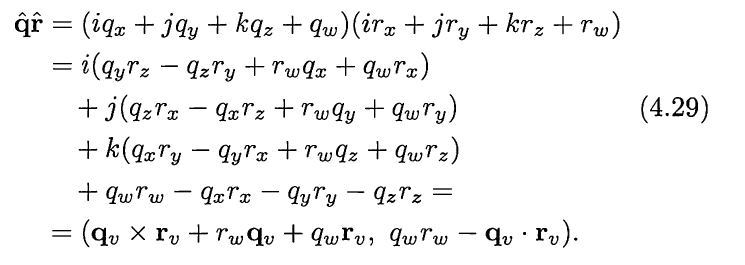

四元数相乘表示旋转,是通过构造p=(v,0),实部为0,表示一个点,
关键点:相乘的形式是qpq*
 ...............................................................式子5.0
...............................................................式子5.0
计算式子5.0利用4.29的形式
实部为0,因为
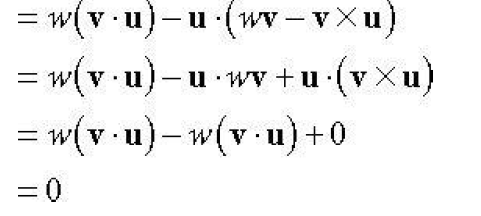
虚部=

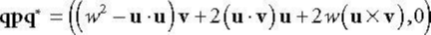

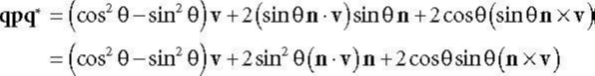
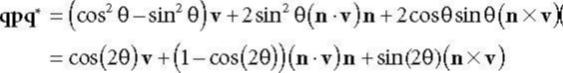
这个式子3.0完全一致,说明了一个四元数p,(v,0)实部为0,v表示为任意向量,顶点的时候,

qpq*表示v绕着q其中的单位向量n,旋转2θ的角度。
矩阵的表达形式:
围绕N(n1,n2,n3)旋转theta角度的OpenGL矩阵为
cosθ,==》c
sinθ===》s
(1-c)n1*n1 +c (1-c)n1*n2-s*n3 (1-c)n1*n3+s*n2
(1-c)n1*n2+s*n3 (1-c)n2*n2+c (1-c)n2*n3-s*n1
(1-c)n1*n3-s*n2 (1-c)*n2*n3+s*n1 (1-c)n3*n3 +c
如果该旋转的四元数表达式为w+xi+yj+zk
那么cos(θ/2)=w,
sin(θ/2)n1=x,
sin(θ/2)n2=y,
sin(θ/2)n3=z,
代入计算,该矩阵为
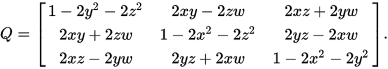


 浙公网安备 33010602011771号
浙公网安备 33010602011771号