UNIQUE VISION Programming Contest 2024 Summer (AtCoder Beginner Contest 359) 题解
A - Count Takahashi
没啥好说的
点击查看代码
#include <bits/stdc++.h>
#define rep(i,n) for(int i=0;i<n;++i)
#define repn(i,n) for(int i=1;i<=n;++i)
#define LL long long
#define fi first
#define se second
#define pb push_back
#define mpr make_pair
void fileio()
{
#ifdef LGS
freopen("in.txt","r",stdin);
freopen("out.txt","w",stdout);
#endif
}
void termin()
{
#ifdef LGS
std::cout<<"\n\nEXECUTION TERMINATED";
#endif
exit(0);
}
using namespace std;
int main()
{
fileio();
int n,ans=0;
string s;
cin>>n;
rep(i,n)
{
cin>>s;
if(s[0]=='T') ++ans;
}
cout<<ans<<endl;
termin();
}
B - Couples
从$1$到$n-2$依次检查第$i$个数和第$i+2$个数是否相同,相同就把答案加一。
时间复杂度$O(n)$。
点击查看代码
#include <bits/stdc++.h>
#define rep(i,n) for(int i=0;i<n;++i)
#define repn(i,n) for(int i=1;i<=n;++i)
#define LL long long
#define fi first
#define se second
#define pb push_back
#define mpr make_pair
void fileio()
{
#ifdef LGS
freopen("in.txt","r",stdin);
freopen("out.txt","w",stdout);
#endif
}
void termin()
{
#ifdef LGS
std::cout<<"\n\nEXECUTION TERMINATED";
#endif
exit(0);
}
using namespace std;
int n,a[210];
int main()
{
fileio();
cin>>n;
rep(i,n*2) cin>>a[i];
int ans=0;
rep(i,n*2-2) if(a[i]==a[i+2]) ++ans;
cout<<ans<<endl;
termin();
}
C - Tile Distance 2
发现我们的最优策略一定是先走到与终点在同一行(y坐标相同),这个过程中尽量缩短横向与终点的距离;到达终点所在行后,再直着走过去。证明:瞪眼法。也就是说我们的路线大概长这样:
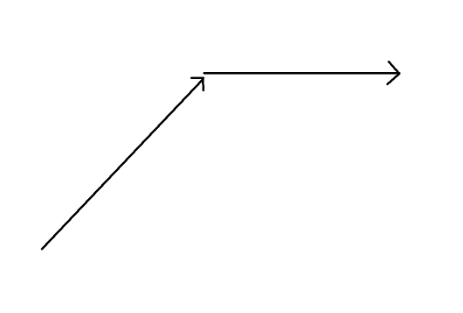
其中斜着的那一段与x轴夹角为45度,这样走可以在把纵向距离缩到0的同时尽量缩短横向距离。令起点和终点的纵向距离为d。走了d步并把纵向距离缩到0后,我们可能到达的砖块是下面这些:
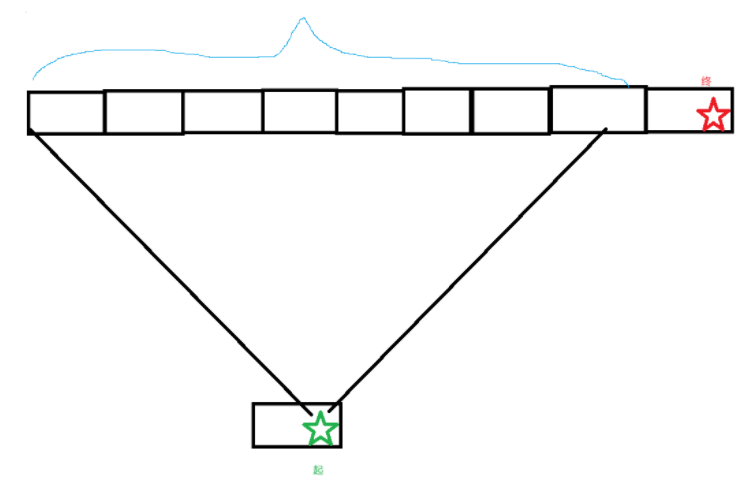
如果终点已经在这些砖块中,那么答案就是d;否则我们就一开始花d步走到这些砖块中离终点最近的,然后横向直着走过去。
时间复杂度$O(1)$。
点击查看代码
#include <bits/stdc++.h>
#define rep(i,n) for(int i=0;i<n;++i)
#define repn(i,n) for(int i=1;i<=n;++i)
#define LL long long
#define pii pair <LL,LL>
#define fi first
#define se second
#define pb push_back
#define mpr make_pair
void fileio()
{
#ifdef LGS
freopen("in.txt","r",stdin);
freopen("out.txt","w",stdout);
#endif
}
void termin()
{
#ifdef LGS
std::cout<<"\n\nEXECUTION TERMINATED";
#endif
exit(0);
}
using namespace std;
pii s,t;
bool same(LL x1,LL y1,LL x2,LL y2)
{
pii aa=mpr(x1,y1),bb=mpr(x2,y2);
if(aa>bb) swap(aa,bb);
return (aa==bb)||(aa.se==bb.se&&aa.fi+1==bb.fi&&(aa.fi+aa.se)%2==0);
}
int main()
{
fileio();
cin>>s.fi>>s.se>>t.fi>>t.se;
LL ans=0;
while(!same(s.fi,s.se,t.fi,t.se))
{
if(s>t) swap(s,t);
if(s.se==t.se)
{
if((s.fi+s.se)%2==0) ++s.fi;
if((t.fi+t.se)%2==1) --t.fi;
LL dist=(t.fi-s.fi-1)/2+1;
ans+=dist;
break;
}
LL dirx=(t.fi>s.fi ? 1:(t.fi==s.fi ? 0:-1)),diry=(t.se>s.se ? 1:(t.se==s.se ? 0:-1)),dist=abs(t.se-s.se);
ans+=dist;
LL ori=s.fi;
s.fi+=dirx*dist;
s.se+=diry*dist;
if(min(ori,s.fi)<t.fi&&t.fi<max(ori,s.fi)) s.fi=t.fi;
}
cout<<ans<<endl;
termin();
}
D - Avoid K Palindrome
令$f_{i,j}$表示处理了前i个位置,从第i个位置往前k个位置的字母组成的bitmask为j的二进制表示的方案数(如果i<k,可以用0填充)。转移时枚举下一位填A(0)还是B(1),计算出新的j(\(nj=(j<<1)\&((1<<k)-1)|newbit\)),然后看一下nj写成k位二进制数是否回文,如果不是就可以转移。
时间复杂度$O(2^kn)$。
点击查看代码
#include <bits/stdc++.h>
#define rep(i,n) for(int i=0;i<n;++i)
#define repn(i,n) for(int i=1;i<=n;++i)
#define LL long long
#define pii pair <int,int>
#define fi first
#define se second
#define pb push_back
#define mpr make_pair
void fileio()
{
#ifdef LGS
freopen("in.txt","r",stdin);
freopen("out.txt","w",stdout);
#endif
}
void termin()
{
#ifdef LGS
std::cout<<"\n\nEXECUTION TERMINATED";
#endif
exit(0);
}
using namespace std;
const int MOD=998244353;
int n,k,bad[1100],dp[1100][1100];
string s;
int main()
{
fileio();
cin>>n>>k>>s;
rep(i,1<<k)
{
string ss="",tt;
int j=i;
rep(p,k)
{
ss+=(j%2+'0');
j/=2;
}
tt=ss;
reverse(tt.begin(),tt.end());
if(ss==tt) bad[i]=1;
}
dp[0][0]=1;
rep(i,n) rep(j,1<<k) if(dp[i][j])
{
//cout<<i<<' '<<j<<' '<<dp[i][j]<<endl;
rep(p,2) if((p==0&&s[i]!='B')||(p==1&&s[i]!='A'))
{
int nj=(j<<1)&((1<<k)-1)|p;
if(i+1<k||!bad[nj]) dp[i+1][nj]=(dp[i+1][nj]+dp[i][j])%MOD;
}
}
int ans=0;
rep(j,1<<k) ans=(ans+dp[n][j])%MOD;
cout<<ans<<endl;
termin();
}
E - Water Tank
拒绝理性思考,拥抱感性猜测(雾。
第i个容器有水的前一刻,所有容器的状态应该是这样:
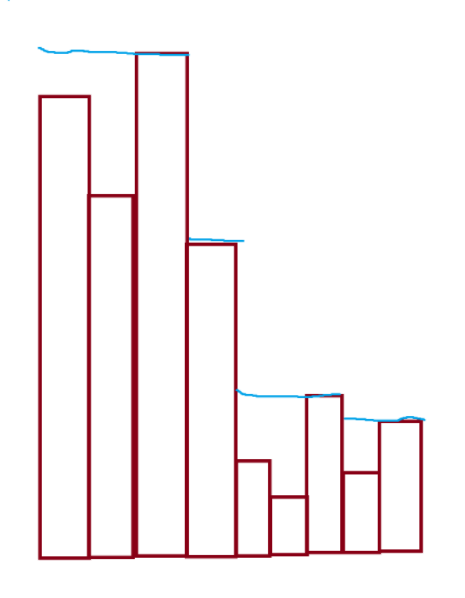
也就是第j个容器中水的高度是$max_{k\in[j,i)}{H_k}$。我们要对每个$i\in[2,n+1]\(求出\)\sum_^max_{k\in[j,i)}{H_k}$。用一个单调栈完美解决。
时间复杂度$O(n)$。
点击查看代码
#include <bits/stdc++.h>
#define rep(i,n) for(int i=0;i<n;++i)
#define repn(i,n) for(int i=1;i<=n;++i)
#define LL long long
#define pii pair <LL,LL>
#define fi first
#define se second
#define pb push_back
#define mpr make_pair
void fileio()
{
#ifdef LGS
freopen("in.txt","r",stdin);
freopen("out.txt","w",stdout);
#endif
}
void termin()
{
#ifdef LGS
std::cout<<"\n\nEXECUTION TERMINATED";
#endif
exit(0);
}
using namespace std;
LL n,a[200010];
stack <pii> q;
pii Front(){return q.empty() ? mpr(-1LL,-1LL):q.top();}
int main()
{
fileio();
cin>>n;
LL ans=0;
rep(i,n)
{
scanf("%lld",a+i);
while(!q.empty()&&q.top().fi<=a[i])
{
pii cur=q.top();q.pop();
pii nxt=Front();
ans-=cur.fi*(cur.se-nxt.se);
}
pii cur=Front();
ans+=a[i]*(i-cur.se);
q.push(mpr(a[i],i));
printf("%lld ",ans+1);
}
cout<<endl;
termin();
}
F - Tree Degree Optimization
注意到如果所有n个节点的度数都>0且和为$2n-2$,那一定存在一棵合法的树。所以只要构造一个满足这个条件的最优的度数序列就可以了。
发现答案不会特别大。比如我们给权值最大的两个点分配度数1,其它点分配度数2,那答案最大就是$4\cdot权值_\cdot n$这个级别。我们先按这个方式分配初始权值,然后通过微小的调整把他调成最优构造。其实一开始怎么分配都行
维护两个堆(可以是set),第一个装所有节点度数+1后会增加的花费以及相应节点的编号;第二个装所有当前分配的度数>1的节点度数-1后会减少的花费以及相应节点的编号。两个堆都按增加/减少的花费为关键字排序。贪心地想,如果第一个堆中的最大元素增加的花费$\geq$第二个堆中的最小元素减少的花费,那怎么调整都不能使花费更小,当前的分配方式就是最优解。否则就把第一个堆中的最大元素度数+1,第二个堆中的最小元素度数-1,然后在两个堆中也做出相应的调整。用瞪眼法看出调整的次数不会超过n次。
时间复杂度$O(nlog_2n)$。
点击查看代码
#include <bits/stdc++.h>
#define rep(i,n) for(int i=0;i<n;++i)
#define repn(i,n) for(int i=1;i<=n;++i)
#define LL long long
#define pii pair <LL,LL>
#define fi first
#define se second
#define pb push_back
#define mpr make_pair
void fileio()
{
#ifdef LGS
freopen("in.txt","r",stdin);
freopen("out.txt","w",stdout);
#endif
}
void termin()
{
#ifdef LGS
std::cout<<"\n\nEXECUTION TERMINATED";
#endif
exit(0);
}
using namespace std;
LL n,a[200010],deg[200010];
set <pii> incs,decs;
LL inc(LL x){return ((deg[x]<<1)|1)*a[x];}
LL dec(LL x){return ((deg[x]<<1)-1)*a[x];}
int main()
{
fileio();
cin>>n;
rep(i,n) scanf("%lld",a+i);
sort(a,a+n);
rep(i,n-2) deg[i]=2;
deg[n-2]=deg[n-1]=1;
rep(i,n)
{
incs.insert(mpr(inc(i),i));
if(deg[i]>1) decs.insert(mpr(dec(i),i));
}
while(!incs.empty()&&!decs.empty())
{
pii d=*decs.rbegin(),i=*incs.begin();
if(d.fi<=i.fi) break;
decs.erase(d);if(incs.find(mpr(inc(d.se),d.se))!=incs.end()) incs.erase(mpr(inc(d.se),d.se));
incs.erase(i);if(decs.find(mpr(dec(i.se),i.se))!=decs.end()) decs.erase(mpr(dec(i.se),i.se));
--deg[d.se];++deg[i.se];
if(deg[d.se]>1) decs.insert(mpr(dec(d.se),d.se));incs.insert(mpr(inc(d.se),d.se));
if(deg[i.se]>1) decs.insert(mpr(dec(i.se),i.se));incs.insert(mpr(inc(i.se),i.se));
}
LL ans=0;
rep(i,n) ans+=a[i]*deg[i]*deg[i];
cout<<ans<<endl;
termin();
}
G - Sum of Tree Distance
这题长的一脸启发式合并的样子。我们随便找一个点作为根开始dfs,并对每个节点维护一个set,其中的元素是一些三元组${颜色,子树中这个颜色的节点个数,子树中所有这个颜色的节点的深度之和}$。其中"颜色"包括了这个子树中出现过的所有颜色。 在搜完当前节点所有子树后,我们来在搞出这个节点对应set的同时计算所有经过这个节点的路径产生的贡献。维护set则用启发式合并,也就是在儿子节点中选择最大的一个set作为"母set",然后把其它儿子的set中的元素加入进去,加入完的set作为当前节点的set。这样总加入次数是$O(nlog_2n)$的。具体实现:令当前节点为pos,set最大的儿子为u,然后swap(s[pos],s[u])(set的swap是O(1)的)。这样空间复杂度也是$O(nlog_2n)$。具体的加入方式就是如果要加入的元素的颜色没有在母set中出现过,就直接插入且不需计算贡献;否则把这个元素和母set中对应颜色的元素合并,然后计算一下这俩元素所代表的对应颜色的节点们互相之间的路径总长,这个用记录的深度之和以及当前节点的深度可以算出来。
时间复杂度$O(nlog_2n)$。
点击查看代码
#include <bits/stdc++.h>
#define rep(i,n) for(int i=0;i<n;++i)
#define repn(i,n) for(int i=1;i<=n;++i)
#define LL long long
#define pii pair <LL,LL>
#define fi first
#define se second
#define pb push_back
#define mpr make_pair
void fileio()
{
#ifdef LGS
freopen("in.txt","r",stdin);
freopen("out.txt","w",stdout);
#endif
}
void termin()
{
#ifdef LGS
std::cout<<"\n\nEXECUTION TERMINATED";
#endif
exit(0);
}
using namespace std;
LL n,a[200010],dep[200010],ans=0;
vector <LL> g[200010];
set <pair <LL,pii> > st[200010];//{color,{count,sum of depths}}
void dfs(LL pos,LL par,LL d)
{
dep[pos]=d;
rep(i,g[pos].size())
{
LL u=g[pos][i];
if(u==par) continue;
dfs(u,pos,d+1);
}
}
void dfs2(LL pos,LL par)
{
st[pos].insert(mpr(a[pos],mpr(1,dep[pos])));
vector <LL> v={pos};
rep(i,g[pos].size()) if(g[pos][i]!=par)
{
dfs2(g[pos][i],pos);
v.pb(g[pos][i]);
}
sort(v.begin(),v.end(),[&](LL x,LL y){return st[x].size()>st[y].size();});
swap(st[pos],st[v[0]]);
rep(i,v.size()) if(v[i]!=pos)
{
LL u=v[i];
for(auto it:st[u])
{
LL col=it.fi,cnt=it.se.fi,sum=it.se.se;
auto it2=st[pos].lower_bound(mpr(col,mpr(0,0)));
if(it2!=st[pos].end()&&it2->fi==col)
{
LL cnt2=it2->se.fi,sum2=it2->se.se;
ans+=cnt*(sum2-dep[pos]*cnt2)+cnt2*(sum-dep[pos]*cnt);
st[pos].erase(it2);
st[pos].insert(mpr(col,mpr(cnt+cnt2,sum+sum2)));
}
else st[pos].insert(it);
}
}
}
int main()
{
fileio();
cin>>n;
LL x,y;
repn(i,n-1)
{
scanf("%lld%lld",&x,&y);
g[x].pb(y);
g[y].pb(x);
}
repn(i,n) scanf("%lld",&a[i]);
dfs(1,0,0);
dfs2(1,0);
cout<<ans<<endl;
termin();
}



