电路布线

电路布线

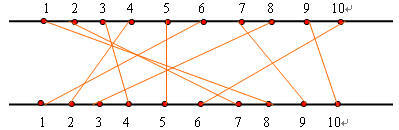
在一块电路板的上、下两端分别有n个接线柱。根据电路设计，要求用导线（i，π(i)）将上端接线柱i与下端接线柱π(i)相连，如图所示。

其中，π(i)，1<=i<=n是{1，2，…，n}的一个排列。导线（i，π(i)）称为该电路板上的第i条连线。对于任何1<=i π(j)。

在制作电路板时，要求将这n条连线分布到若干绝缘层上。在同一层上的连线不相交。你的任务是要确定将哪些连线安排在第一层上，使得该层上有尽可能多的连线。换句话说，就是确定导线集Nets={ i，π(i)，1<=i<=n}的最大不相交子集。

 

今天看书实在看不下去，闲得无聊随手拿了本算法书以乱心智。心烦地的乱翻，最后停在了这道题目上。一开始没有看题解，一通胡思乱想之后，设法证明自己的想法是正确，结果失败了。这里的失败是说未能给证明，并不是指我算法的正确与否。回来调试，又是几个小case错误外。。。上网一搜，网上的文章一大抄，都是书的一样的算法（见附录）。。。。

思想来源上次看到的一道题目: 谁看的最多。

算法思想：

。。。。懒得写，迟点再写。。。

隐约地觉得算法是正确的。但是，现在还没有证明。其实更隐约地觉得其实我的思路里已经蕴含了它的思想。。。

#include<iostream>
#include<malloc.h>

using namespace std;

int func17(int b[], int n)
{
    int *c; //c[i]记录上排线0到i-1中的连线不相交的最大集合
    int *d; //d[i]记录i阶段的选择 若无,则为-1
    int bigpos; //当前最大值得下标, 若有相同的最大值,择选b[]小的
    int i,j;

    if (n<=0)
    {
        return 0;
    }
    c = (int *)malloc(sizeof(int)*n);
    d= (int *)malloc(sizeof(int)*n);
    
    c[0] =1;
    d[0] = -1;
    bigpos = 0;

    for (i=0; i<n; i++)
    {
        for (j=bigpos; j!=-1;)
        {
            if (b[j] <b[i])
            {
                break;
            }
            else
            {
                j = d[j];
            }
        }
        if (j==-1)
        {
            c[i] =1;
            d[i] =-1;

        }
        else
        {
            c[i] = c[j]+1;
            d[i] = j;
        }
        if (c[i]> c[bigpos] || (c[i]==c[bigpos] && b[i]<b[bigpos]))
        {
            bigpos = i;
        }
    }

    int tmp = c[bigpos];
    
    free(c);
    free(d);

    return tmp;
}

int main()
{
        int a[] = {8,7,4,2,5,1,9,3,10};

    cout<<func17(a, sizeof(a)/sizeof(int))<<endl;;

    return 0;
}

附录：

问题分析：

1.       最优子结构性质

记N(i,j) = {t|(t, π(i)) ∈ Nets,t ≤ i, π(t) ≤ j }. N(i,j)的最大不相交子集为MNS（i,j）。Size(i,j)=|MNS(i,j)|。 

    1） 当i = 1时

 

2)       当i >1时，

①       j <π(i)。此时，(i,π(i)) 不属于N(i,j)。故在这种情况下，N(i,j) = N(i-1,j)，从而Size(i,j)=Size(i-1,j).

②       j ≥π(i)。此时，若(i, π(i))∈MNS(i,j)，则对任意(t, π(i))∈MNS(i,j)有t < i且π(t)< π(i)；否则，(t, π(t))与(i, π(i))相交。在这种情况下MNS(i,j)-{(i, π(i))}是N(i-1, π(i)-1)的最大不相交子集。否则，子集MNS(i-1, π(i)-1)∪{(i, π(i))}包含于N(i,j)是比MNS(i,j)更大的N(i,j)的不相交子集。这与MNS(i,j)的定义相矛盾。

若(i, π(i))不属于MNS(i,j)，则对任意(t, π(t))∈MNS(i,j)，有t<i。从而MNS(i,j)包含于N(i-1,j)，因此，Size(i,j)≤Size(i-1,j).

另一方面，MNS(i-1,j)包含于N(i,j),故又有Size(i,j) ≥Size(i-1,j)，从而Size（i,j）= Size(i-1,j).

2.       递归计算最优值

经以上后分，可电路布线问题的最优值为Size(n,n)。由该问题的最优子结构性质可知： 

 

 

毕