0-1背包问题的分枝—限界算法
1.分枝—限界法的基本原理 分枝—限界算法类似于回溯法,也是一种在问题的解空间树上搜索问题解的算法。但两者求解方法有两点不同:第一,回溯法只通过约束条件剪去非可行解,而分枝—限界法不仅通过约束条件,而且通过目标函数的限界来减少无效搜索,也就是剪掉了某些不包含最优解的可行解;第二,在解空间树上,回溯法以深度优先搜索,而分枝—限界法则以广度优先或最小耗费优先的方式搜索。分枝—限界的搜索策略是,在扩展节点处,首先生成其所有的儿子结点(分支),然后再从当前的活结点表中选择下一个扩展结点。为了有效地选择下一扩展结点,以加速搜索进程,在每一活结点处,计算一个函数值(限界),并根据这些已计算出的函数值从当前活结点表中选择一个最有利的结点做为扩展,使搜索朝着解空间树上最优解的分支推进,以便尽快找出一个最优解。 分枝—限界法常以广度优先或以最小耗费优先的方式搜索问题的解空间树(问题的解空间树是表示问题皆空间的一颗有序树,常见的有子集树和排序树)。在搜索问题的解空间树时,分枝—限界法的每一个活结点只有一次机会成为扩展结点。活结点一旦成为扩展结点,就一次性产生其所有儿子结点。在这些儿子结点中,那些导致不可行解或非最优解的儿子结点将被舍弃,其余儿子结点被加入活结点表中。此后,从活结点表取出下一结点成为当前扩展结点,并重复上述扩展过程,直到找到最优解或活结点表为空时停止。 2. 0-1背包问题的分枝—限界算法的数据结构 template<class Typew,class Typep> class HeapNode { friend Knap<Typew,Typep>; public: operator Typep() const { return uprofit; } private: Typep uprofit, //节点的价值上界 profit; //节点所相应的价值 Typew weight; //节点所相应的重量 int level; //活节点在子集树中所处的层序号 bbnode *ptr; //指向活节点在子集中相应节点的指针 }; 3. 限界函数: Typep Knap<Typew,Typep>::Bound(int i)//计算节点所相应价值的上界 { Typew cleft = c-cw; //剩余容量高 Typep b = cp; //价值上界 //以物品单位重量价值递减序装填剩余容量 while(i<=n && w[i]<=cleft) { cleft -= w[i]; b += p[i]; i++; } 4.算法具体实现主要代码如下: //0-1背包问题 分支限界法求解 #include "stdafx.h" #include "MaxHeap.h" #include <iostream> using namespace std; class Object { template<class Typew,class Typep> friend Typep Knapsack(Typep p[],Typew w[],Typew c,int n, int bestx[]); public: int operator <= (Object a) const { return d>=a.d; } private: int ID; float d;//单位重量价值 };
template<class Typew,class Typep> class Knap;
class bbnode { friend Knap<int,int>; template<class Typew,class Typep> friend Typep Knapsack(Typep p[],Typew w[],Typew c,int n, int bestx[]); private: bbnode * parent; //指向父节点的指针 bool LChild; //左儿子节点标识 };
template<class Typew,class Typep> class HeapNode { friend Knap<Typew,Typep>; public: operator Typep() const { return uprofit; } private: Typep uprofit, //节点的价值上界 profit; //节点所相应的价值 Typew weight; //节点所相应的重量 int level; //活节点在子集树中所处的层序号 bbnode *ptr; //指向活节点在子集中相应节点的指针 };
template<class Typew,class Typep> class Knap { template<class Typew,class Typep> friend Typep Knapsack(Typep p[],Typew w[],Typew c,int n, int bestx[]); public: Typep MaxKnapsack(); private: MaxHeap<HeapNode<Typep,Typew>> *H; Typep Bound(int i); void AddLiveNode(Typep up,Typep cp,Typew cw,bool ch,int lev);
bbnode *E; //指向扩展节点的指针 Typew c; //背包容量 int n; //物品数
Typew *w; //物品重量数组 Typep *p; //物品价值数组 Typew cw; //当前重量
Typep cp; //当前价值 int *bestx; //最优解 };
template <class Type> inline void Swap(Type &a,Type &b);
template<class Type> void BubbleSort(Type a[],int n);
int main() { int n = 3;//物品数 int c = 30;//背包容量 int p[] = {0,45,25,25};//物品价值 下标从1开始 int w[] = {0,16,15,15};//物品重量 下标从1开始 int bestx[4];//最优解
cout<<"背包容量为:"<<c<<endl; cout<<"物品重量和价值分别为:"<<endl;
for(int i=1; i<=n; i++) { cout<<"("<<w[i]<<","<<p[i]<<") "; } cout<<endl;
cout<<"背包能装下的最大价值为:"<<Knapsack(p,w,c,n,bestx)<<endl; cout<<"此背包问题最优解为:"<<endl; for(int i=1; i<=n; i++) { cout<<bestx[i]<<" "; } cout<<endl; return 0; }
template<class Typew,class Typep> Typep Knap<Typew,Typep>::Bound(int i)//计算节点所相应价值的上界 { Typew cleft = c-cw; //剩余容量高 Typep b = cp; //价值上界 //以物品单位重量价值递减序装填剩余容量 while(i<=n && w[i]<=cleft) { cleft -= w[i]; b += p[i]; i++; }
//装填剩余容量装满背包 if(i<=n) { b += p[i]/w[i]*cleft; }
return b; }
//将一个活节点插入到子集树和优先队列中 template<class Typew,class Typep> void Knap<Typew,Typep>::AddLiveNode(Typep up,Typep cp,Typew cw,bool ch,int lev) { bbnode *b = new bbnode; b->parent = E; b->LChild = ch;
HeapNode<Typep,Typew> N; N.uprofit = up; N.profit = cp; N.weight = cw; N.level = lev; N.ptr = b;
H->Insert(N); }
//优先队列式分支限界法,返回最大价值,bestx返回最优解 template<class Typew,class Typep> Typep Knap<Typew,Typep>::MaxKnapsack() { H = new MaxHeap<HeapNode<Typep,Typew>>(1000);
//为bestx分配存储空间 bestx = new int[n+1];
//初始化 int i = 1; E = 0; cw = cp = 0; Typep bestp = 0;//当前最优值 Typep up = Bound(1); //价值上界
//搜索子集空间树 while(i!=n+1) { //检查当前扩展节点的左儿子节点 Typew wt = cw + w[i]; if(wt <= c)//左儿子节点为可行节点 { if(cp+p[i]>bestp) { bestp = cp + p[i]; } AddLiveNode(up,cp+p[i],cw+w[i],true,i+1); }
up = Bound(i+1); //检查当前扩展节点的右儿子节点 if(up>=bestp)//右子树可能含有最优解 { AddLiveNode(up,cp,cw,false,i+1); }
//取下一扩展节点 HeapNode<Typep,Typew> N; H->DeleteMax(N); E = N.ptr; cw = N.weight; cp = N.profit; up = N.uprofit; i = N.level; }
//构造当前最优解 for(int j=n; j>0; j--) { bestx[j] = E->LChild; E = E->parent; } return cp; }
//返回最大价值,bestx返回最优解 template<class Typew,class Typep> Typep Knapsack(Typep p[],Typew w[],Typew c,int n, int bestx[]) { //初始化 Typew W = 0; //装包物品重量 Typep P = 0; //装包物品价值
//定义依单位重量价值排序的物品数组 Object *Q = new Object[n]; for(int i=1; i<=n; i++) { //单位重量价值数组 Q[i-1].ID = i; Q[i-1].d = 1.0*p[i]/w[i]; P += p[i]; W += w[i]; }
if(W<=c) { return P;//所有物品装包 }
//依单位价值重量排序 BubbleSort(Q,n);
//创建类Knap的数据成员 Knap<Typew,Typep> K; K.p = new Typep[n+1]; K.w = new Typew[n+1];
for(int i=1; i<=n; i++) { K.p[i] = p[Q[i-1].ID]; K.w[i] = w[Q[i-1].ID]; }
K.cp = 0; K.cw = 0; K.c = c; K.n = n;
//调用MaxKnapsack求问题的最优解 Typep bestp = K.MaxKnapsack(); for(int j=1; j<=n; j++) { bestx[Q[j-1].ID] = K.bestx[j]; }
delete Q; delete []K.w; delete []K.p; delete []K.bestx; return bestp; } template<class Type> void BubbleSort(Type a[],int n) { //记录一次遍历中是否有元素的交换 bool exchange; for(int i=0; i<n-1;i++) { exchange = false ; for(int j=i+1; j<=n-1; j++) { if(a[j]<=a[j-1]) { Swap(a[j],a[j-1]); exchange = true; } } //如果这次遍历没有元素的交换,那么排序结束 if(false == exchange) { break ; } } }
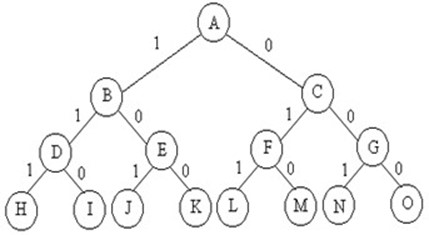
template <class Type> inline void Swap(Type &a,Type &b) { Type temp = a; a = b; b = temp; } 编译并运行程序。 5. 0-1背包问题的分枝—限界算法的搜索过程与解空间树 当n=3时,w={16,15,15}, p={45,25,25}, c=30。优先队列式分支限界法:处理法则:价值大者优先。{}—>{A}—>{B,C}—>{C,D,E}—>{C,E}—>{C,J,K}—>{C}—>{F,G}—>{G,L,M}—>{G,M}—>{G}—>{N,O}—>{O}—>{}
6.算法的时间复杂性和空间复杂性
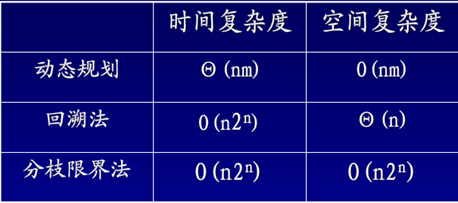
0-1背包问题不同算法时间复杂性和空间复杂性的比较 0-1背包问题的分枝—限界算法的时间复杂度为:O(n*2n),空间复杂度为:O(nm), 0-1背包问题的回溯法时间复杂度为:O(n*2n),与分枝—限界算法相同,而空间复杂度与分枝—限界算法不同,为:θ(n)。 |
测试数据: 背包容量为30 物品重量和价值分别为: 16,45 15,25 15,25 程序运行结果如下:
为了方便只取了一组简单的测试数据,可能会对实验结果造成影响,后面还要取更多的数据进行测试。 |





 浙公网安备 33010602011771号
浙公网安备 33010602011771号