线性代数 | Linear Algebra
网上说《线性代数应该这样学》非常不错，再配合大学教材，把线性代数的基本知识点过一遍。
线性代数 - 知乎
最近在跟一个教程：李宏毅的线性代数
基本知识：
Rn :We denote the set of all vectors with n entries by Rn .
We use Mmxn to denote the set that contains all matrices whose size is m x n
Identity matrix: must be square • 對角線是 1, 其它都是 0
Transpose：𝐴 𝑇 (transpose of A) is an nxm matrix whose (i,j)- entry is the (j-i)-entry of A
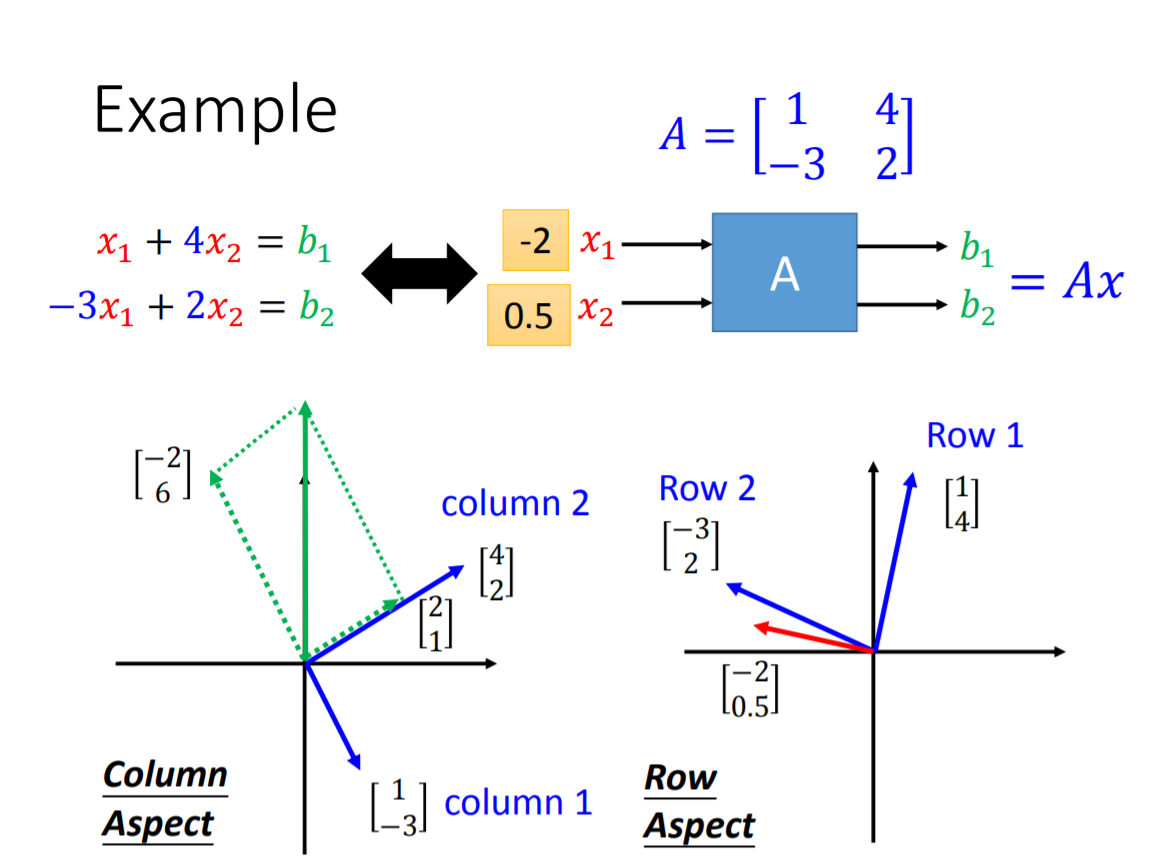
Matrix-Vector Product：乘法。Row Aspect，column aspect。
A and B aremxn matrices. If 𝐴𝑤 = 𝐵𝑤 for all 𝑤 inRn . Is it true that 𝐴 = 𝐵? 可以用于检测两个线性系统是否相同。
linear combination：列向量的线性公式。Ax = b，能否通过A和x的linear combination得到b 等价于 有没有解。在二维空间，两个不平行的非零向量可以通过linear combination形成空间中的所有向量。三维同理。
span：Span of 𝑆 is the vector set of all linear combinations of 𝑢1, 𝑢2,⋯ , 𝑢𝑘. Denoted by 𝑆𝑝𝑎𝑛 𝑢1, 𝑢2,⋯ , 𝑢𝑘 or S𝑝𝑎𝑛 𝑆. 一个向量的所有线性组合。在span里就有解。
总结：Is 𝑏 a linear combination of columns of 𝐴? OR Is 𝑏 in the span of the columns of 𝐴? Have solution （线性组合不就是吧Ax=b换了个说法吗？Ax=b，这里x可能不存在；但是如果能够线性组合就是说Ax=b，但是这个x是存在的。所以线性组合没有解决任何问题啊，只是重新换了个定义而已。）
现在假设已经有解了，我想知道有唯一解还是无穷解。
consistent：有一个及一个以上的解；inconsistent：没有解；row aspect：线或者面是否有交点；
Linear Dependent：对象是vector的集合，也就是A。Given a vector set, {a1, a2, , an}, if there exists any ai that is a linear combination of other vectors.
homogeneous equation：Ax=0
另一种描述：A set of n vectors 𝒂𝟏, 𝒂𝟐, ⋯ , 𝒂𝒏 is linear independent. Only scalars such that: 𝑥1𝒂𝟏 + 𝑥2𝒂𝟐 + ⋯ + 𝑥𝑛𝒂𝒏 = 𝟎, Only if 𝑥1 = 𝑥2 = ⋯ = 𝑥𝑘 = 0
如果存在一个不为零的系数，则说明是Linear Dependent。逆反一下，如果所有系数都为0才能使Ax=0，说明这是Linear inDependent。
rank: the maximum number of linearly independent columns in the matrix
Nullity = Number of columns - rank
If the columns of A are linear independent, then Ax=b has at most one solution. 虽然每个列向量都是独立的，但是还是有可能没有解。
If the columns of A are linear independent, then Ax=0 (homogeneous equation) has unique solution. 是有唯一解，那就是0.
总结：linear equations有没有解，𝑏 is in the span of the columns of 𝐴, 则有至少一个解。The columns of 𝐴 are independent，则等价于Rank A = n and Nullity A = 0，有Unique solution；否则就有无数个解。
发现有解了，现在怎么解？
equivalent的线性方程组。
Augmented Matrix：合并A和b
Row Echelon Form：零row在最下面；leading entries是 Echelon Form
Reduced Row Echelon Form：The columns containing the leading entries are standard vectors.
Gaussian elimination：elementary row operations.
RREF: Reduced Row Echelon Form.
Columns:
• The relations between the columns are the
same.
• The span of the columns is different.
• Rows:
• The relations between the rows are changed.
• The span of the rows is the same.
1 矩阵
2 矩阵的初等变换与线性方程组
3 向量组的线性相关性
4 矩阵的对角化与二次型
5 线性规划问题
6 单纯型方法
待续~
