实战中的贝叶斯
贝叶斯，人人都学过一点，大部分人都以为自己懂了，不就是一个条件概率公式吗，其实还真没那么简单，想完全学通弄透还是要花点力气的
下面的都是你必须弄懂的：
- 怎么用常识解释贝叶斯公式？
- 什么是先验，什么是后验，它们在贝叶斯公式中如何体现，如何解释贝叶斯定理中的每一项？
- 贝叶斯学派的核心思想，它与其他派的区别？ 贝叶斯的优势与不足？
- 最大似然、贝叶斯和最大后验的区别与联系？
- (|)=(|)怎么理解？
- 贝叶斯和机器学习有什么关系？
- 实战中如何运用贝叶斯？
- 复杂情况下的贝叶斯
贝叶斯学派和频率学派的区别之一是特别重视先验信息对于inference的影响。
我们的概率主要有如下几种：P(θ)（先验分布）, p(θ|X)（后验分布）, p(X), p(X|θ) （似然函数）
它们之间的关系可以通过贝叶斯公式进行连接： 后验分布 = 似然函数* 先验分布/ P(X)
之所以采用共轭先验的原因是可以使得先验分布和后验分布的形式相同，这样一方面合符人的直观（它们应该是相同形式的）另外一方面是可以形成一个先验链，即现在的后验分布可以作为下一次计算的先验分布，如果形式相同，就可以形成一个链条。
如果先验分布和似然函数可以使得先验分布和后验分布有相同的形式，那么就称先验分布与似然函数是共轭的。
先理清楚概率论中的三个重要公式：
1.贝叶斯公式：
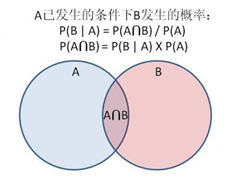
P(A∩B) = P(A)*P(B|A) = P(B)*P(A|B)
P(B|A) = P(A|B)*P(B) / P(A)
其中P(B|A) 和P(A|B)分别为后验概率和先验概率（不同样本空间的问题）都是后验概率，P(A)和P(B)才是先验，先验是任何我们已知的或者假设的， 贝叶斯就是根据已知来求未知。（这么解释是绝对错误的）
就是两个事件同时发生的概率，等于其中一个事件发生的概率，乘以该事件发生概率下另一个事件发生的概率，这里只要求两个事件相互独立（相互独立不等于互斥）。这个模型可以推广到生活中任意的两个相互独立的事件上，韦恩图是直观的展示。
这个公式最大的用处就是恒等带来的额外的作用，我们很容易得到一个先验知识，但我们想要的是另外一个东西，叫做后验知识，在韦恩图中，我们已知P(B|A) ，但我们不知道P(A|B)，即右边粉红的图实际上是一个动态的图。
为什么实验越完备，贝叶斯公式中的先验就越不重要？
为什么说贝叶斯是根据实验所得对我们已知的知识进行修正的模型？
小知识：条件概率可以认为是缩小了样本空间之后的概率。
2.全概率公式：
公式表示若事件A1，A2，…，An构成一个完备事件组且都有正概率，则对任意一个事件B都有公式成立。
全概率公式就是最基本的加法公式，将样本空间合理分割，最后再加起来。
贝叶斯公式是全概率公式的逆运算
3.乘法公式：
P(AB) = P(A|B)P(B)
相互独立事件的运算，相互独立的由来？相互独立的运用？独立与相关？
微信上看到一篇贝叶斯的绝世好文：参数估计：最大似然、贝叶斯与最大后验
实际中，在序列问题上，对于某一个位点，有两个事件，一是该位点出现我们这个观察值及其他的概率P(obs,n,R,S)，一是我们这个位点出现某个特定genotype的概率P(g)。
我们真正想要的是P(g|obs,n,R,S)，即该位点观察值为obs等等时，出现g的概率，这个是我们的后验，我们不知道。我们知道的是P(obs,n,R,S|g)，即真实情况下，出现这些的概率，这个是我们的先验。
我们的先验有：预先知道的该位点的n、R、S、突变率。
我们求得的最大后验就可以看做是该位点真实的genotype。
整个过程我们借用了ref来group reads？还借用了GATK的call genotype功能，PL列就是该位点的基因型genotype及其likelihood。
Question: How to interpret genotype likelihoods?
PL is log10-scaled and normalized
Likelihood ratio = Likelihood(most likely genotype)/(Likelihood(alternative genotype 1) + Likelihood(alternative genotype 2)
Genotype likelihood and QUAL – GATK
PL = -10 * log[P(Data|Genotype)]
HC step 4: Assigning per-sample genotypes
概率（probability)、似然（likelihood)、极大似然法
概率是给定某一参数值，求某一结果的可能性。
似然是给定某一结果，求某一参数值的可能。最大似然法就是用来求最优参数的！可以一个一个试，也可以直接用极大似然函数求解：
L(x1,x2……xn,p)=C(N,x1)*C(N,x2)……*C(N,xn)*p^(∑xi)*(1-p)^(Nn-∑xi)；
取对数ln L=ln(C(N,x1)*C(N,x2)……*C(N,xn))+(∑xi)lnp+(Nn-∑xi)ln(1-p)；对p求导；d(ln L)/dp=(∑xi)/p-(Nn-∑xi)/(1-p)；在p=(∑xi)/Nn时，d(ln L)/dp=0，且此时L取最大值；所以p的极大似然估计是p=(∑xi)/Nn=26/50=0.52(与真实值0.5相比，误差很小）
基本所有的变化都是围绕这三个公式展开，我还是只能看懂，什么时候自己能将他熟练的运用到实际中呢？
概率与似然 同一篇文章，不同时候来读果然感觉不一样，尤其在这个方面。
看文章有感：
条件概率，P(A|B)表示在B事件发生的情况下，A事件发生的概率，就是样本空间缩小到B，再计算A发生的概率
先验和后验是相对的，根据我们已有的经验得到的就是先验，先验一般不是条件概率如P(A)；后验就是条件概率如P(A|B)
Bayes法则：后验概率 = 标准相似度 * 先验概率 （贝叶斯法则，先验概率与后验概率的区别）
后验概率( posterior probability)是指在得到“结果”的信息后重新修正的概率,如贝叶斯公式中的,是“执果寻因”问题中的“因”。
首先打好2个基础
1.这两类均是由2个阶段组成
2.条件概率的思想
1.全概公式：首先建立一个完备事件组的思想,其实全概就是已知第一阶段求第二阶段,比如第一阶段分A B C三种,然后A B C中均有D发生的概率,最后让你求D的概率
P(D)=P(A)*P(D/A）+P(B)*P(D/B）+P(C)*P(D/C）
2.贝叶斯公式,其实原本应该叫逆概公式,为了纪念贝叶斯这样取名而已.在全概公式理解的基础上,贝叶斯其实就是已知第二阶段反推第一阶段,这时候关键是利用条件概率公式做个乾坤大挪移,跟上面建立的A B C D模型一样,已知P(D),求是在A发生下D发生的概率,这就是贝叶斯
P(A/D)=P(AD)/P(D)=P(A)*P(D/A)/P(D)
§1.6全概率公式与贝叶斯公式 （例子讲得很好）
经典文章：从贝叶斯方法谈到贝叶斯网络
