信息论 | information theory | 信息度量 | information measures | R代码（一）

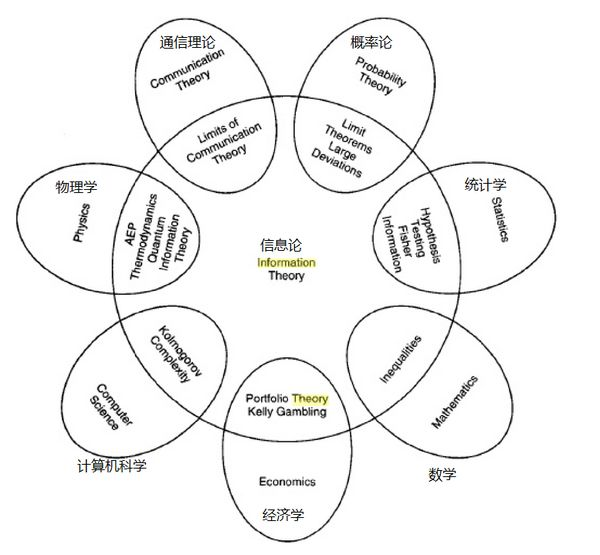
这个时代已经是多学科相互渗透的时代，纯粹的传统学科在没落，新兴的交叉学科在不断兴起。

life science
neurosciences
statistics
computer science
information theory

我的问题很简单：

一个细胞里到底保存了多少信息，复制、转录、翻译过程中传递了多少信息？
神经突触传递信息的上限是多少？

想回答这些问题就必须要学习信息论！

什么是信息？

两个同样的光碟里保存的信息是一样的吗？

人和信息的关系是什么？假设所有人都不存在了，信息还存在吗？

independence of random variables

Mutual Independence
Pairwise Independence
Conditional Independence

Markov chain

strictly positive

重点概念：

条件独立：独立与条件独立，X->Y->Z，X与Y不独立，Y与Z也不独立，X与Z呢？这就是条件独立。也就是X和Z的依赖关系（独立关系）借由Y产生，所以叫条件独立。举例：X：明天下雨，Y：今天下雨，Z：今天地面变湿了。

马尔科夫链：由条件独立引申而来。𝑝(𝑋1,𝑋2,…,𝑋𝑛)=𝑝(𝑋1)𝑝(𝑋1∣𝑋2)𝑝(𝑋2∣𝑋3)…𝑝(𝑋𝑛−1∣𝑋𝑛)。马尔科夫链其实并不是严格的链，也有可能是环。小白都能看懂的马尔可夫链详解

马尔科夫子链：任意从马尔科夫链中取出m个节点，按顺序排列，新的马尔科夫链是原来的一个子链。（有点难以理解，明明断开了）

entropy

conditional entropy

mutual information

conditional mutual information

熵的数学定义：

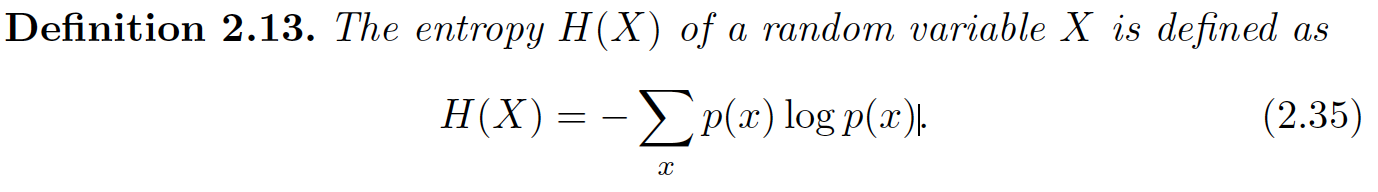
和概率分布一样，熵也是随机变量的函数，更确切的说，熵是概率分布的函数。

此时我们讨论的都是离散随机变量，所以只能选离散分布来计算熵值。

可以看到，对于伯努利分布而言，当0和1出现概率都为0.5时，此时随机变量的概率分布的熵值最大，为1.

library(philentropy)
library(ggplot2)
library(Rlab)

# define probabilities P(X)
Prob <- 1:10/sum(1:10)
# Compute Shannon's Entropy
H(Prob)

x <- (0:1000)/1000
y <- unlist(lapply(x, function(x) {H(dbern(0:1, x))}))
ggplot(data=data.frame(prob=x, entropy=y), aes(x=prob, y=entropy)) + 
  geom_bar(stat="identity") + 
  labs(title = "Entropy of Bernoulli Distribution") +
  geom_hline(yintercept=0) +
  geom_vline(xintercept=0)

H(dbinom(1:100, size = 100, prob = 0.1))
H(dbinom(1:100, size = 100, prob = 0.3))
H(dbinom(1:100, size = 100, prob = 0.5))
H(dbinom(1:100, size = 100, prob = 0.7))
H(dbinom(1:1000, size = 100, prob = 0.7))
H(dbinom(1:1000, size = 1000, prob = 0.7))
ggplot(data=data.frame(x=1:100, probability=dbinom(1:100, size = 100, prob = 0.7)), 
                aes(x=x, y=probability)) + geom_bar(stat="identity")
ggplot(data=data.frame(x=1:1000, probability=dbinom(1:1000, size = 100, prob = 0.7)), 
       aes(x=x, y=probability)) + geom_bar(stat="identity")
ggplot(data=data.frame(x=1:1000, probability=dbinom(1:1000, size = 1000, prob = 0.7)), 
       aes(x=x, y=probability)) + geom_bar(stat="identity")

为什么香农选的是这个公式？

代码可以参考我之前文章：统计分布汇总 | 生物信息学应用 | R代码 | Univariate distribution relationships

可以看到熵值函数是一个求和函数，基本单位是-p*log(p), 其中0<=p<=1. 所有的p值之和为1.

可以将这个基本函数可视化：

可以看到这并不是一个对称函数，极值在x=0.3678694时取得，为0.5307378。

h <- function(x) {-x*log2(x)}
curve(h, 0, 1) + abline(v=0.3678694, h=0.5307378)
plot(h) + abline(v=0.3678694, h=0.5307378)
# h=0.5307378

optimize(h, c(0,1), maximum = T)
# nlm(h, c(0,1))

如何证明，对所有的p(x)的概率分布，h(x)的最大值都是在所有事件等概论时出现？相当于离散型的均匀分布。

最优化问题的求解与R实现

code alphabet - 决定了熵值函数里面的基

Shannon的熵值公式也可以用期望的角度来解读