leetcode题解之51. N皇后

n 皇后问题研究的是如何将 n 个皇后放置在 n×n 的棋盘上，并且使皇后彼此之间不能相互攻击。

上图为 8 皇后问题的一种解法。

给定一个整数 n，返回所有不同的 n 皇后问题的解决方案。

每一种解法包含一个明确的 n 皇后问题的棋子放置方案，该方案中 'Q' 和 '.' 分别代表了皇后和空位。

示例:

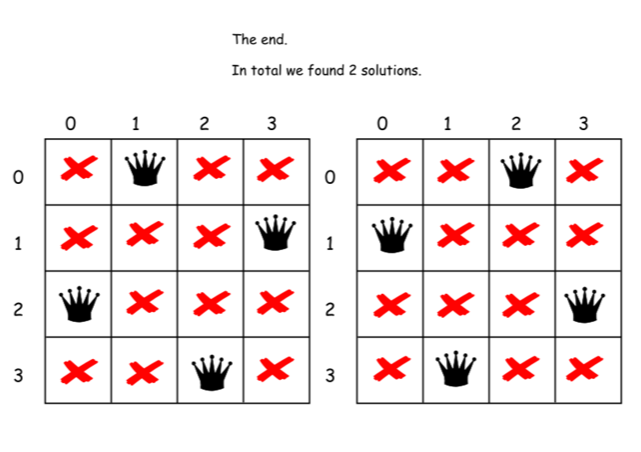
输入: 4
输出: [
 [".Q..",  // 解法 1
  "...Q",
  "Q...",
  "..Q."],

 ["..Q.",  // 解法 2
  "Q...",
  "...Q",
  ".Q.."]
]
解释: 4 皇后问题存在两个不同的解法。

 

提示：

• 皇后，是国际象棋中的棋子，意味着国王的妻子。皇后只做一件事，那就是“吃子”。当她遇见可以吃的棋子时，就迅速冲上去吃掉棋子。当然，她横、竖、斜都可走一到七步，可进可退。（引用自 百度百科 - 皇后 ）

直观想法

第一个想法是使用蛮力法，意味着生成在棋盘上放置 N 个皇后的所有可能的情况，并且检查是否保证没有皇后可以互相攻击。这意味着 $\mathcal{O}(N^N)$ 的时间复杂度，因此我们必须考虑优化。

下面是两个有用的编程概念。

第一个叫做 约束编程.

它的基本含义是在放置每个皇后以后增加限制。当在棋盘上放置了一个皇后后，立即排除当前行，列和对应的两个对角线。该过程传递了 约束 从而有助于减少需要考虑情况数。

第二个叫做 回溯法.

我们来想象一下，当在棋盘上放置了几个皇后且不会相互攻击。但是选择的方案不是最优的，因为无法放置下一个皇后。此时我们该怎么做？回溯。意思是回退一步，来改变最后放置皇后的位置并且接着往下放置。如果还是不行，再 回溯。

---

方法1：回溯

在建立算法之前，我们来考虑两个有用的细节。

一行只可能有一个皇后且一列也只可能有一个皇后。

这意味着没有必要再棋盘上考虑所有的方格。只需要按列循环即可。

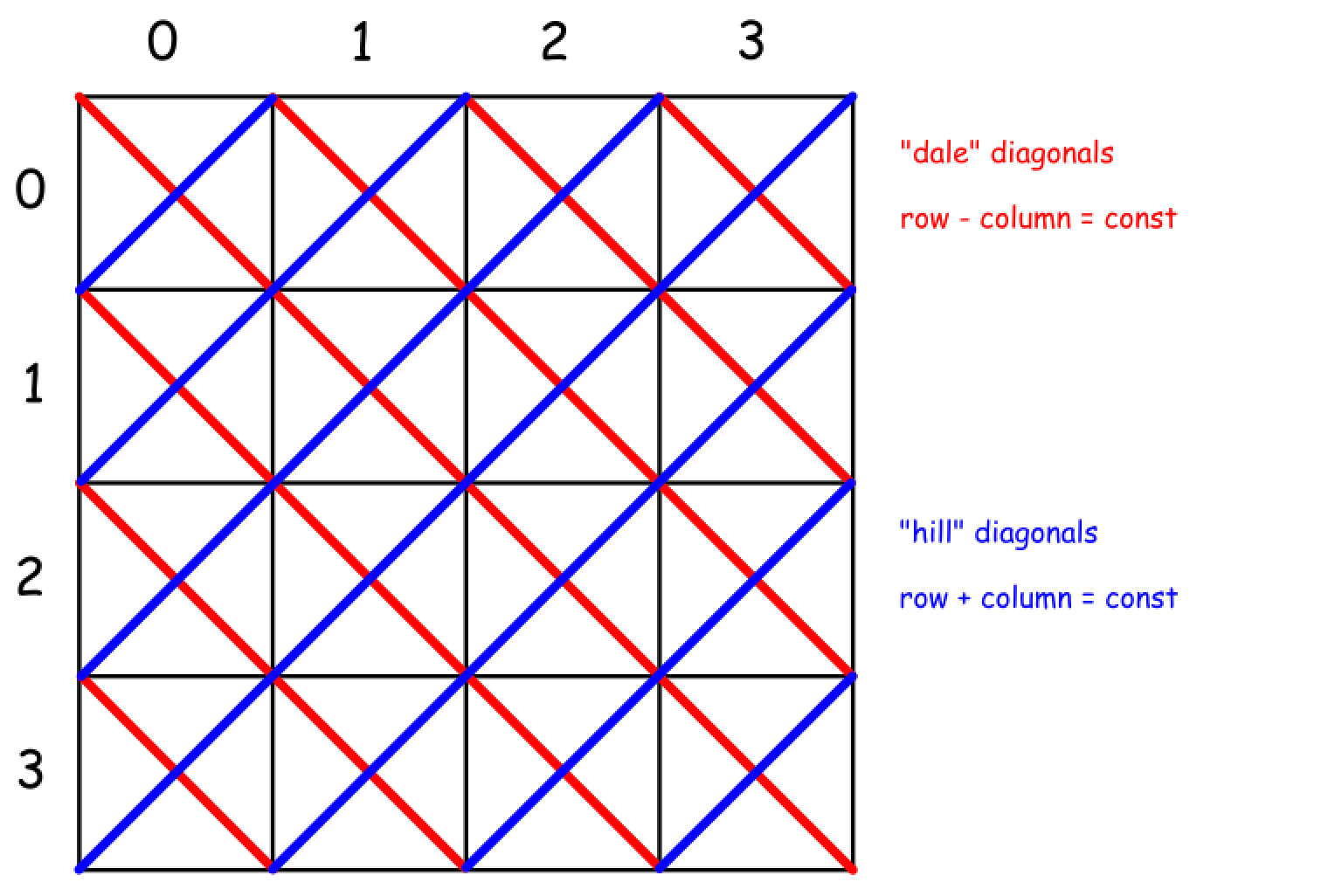
对于所有的主对角线有 行号 + 列号 = 常数，对于所有的次对角线有 行号 - 列号 = 常数.

这可以让我们标记已经在攻击范围下的对角线并且检查一个方格 (行号, 列号) 是否处在攻击位置。

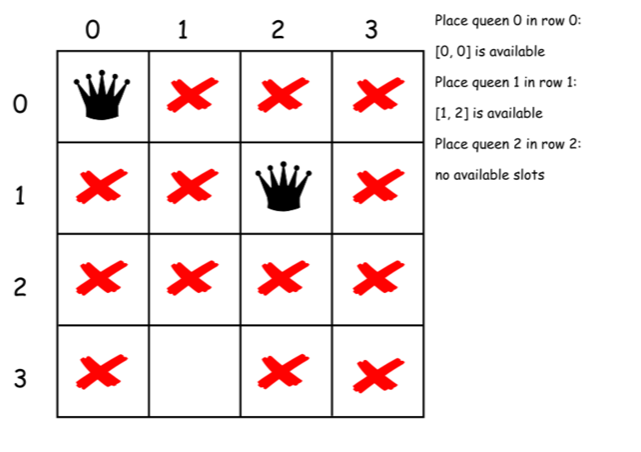
现在已经可以写回溯函数 backtrack(row = 0).

• 从第一个 row = 0 开始.

• 循环列并且试图在每个 column 中放置皇后.

  • 如果方格 (row, column) 不在攻击范围内

    • 在 (row, column) 方格上放置皇后。
    • 排除对应行，列和两个对角线的位置。
    • If 所有的行被考虑过，row == N
      • 意味着我们找到了一个解
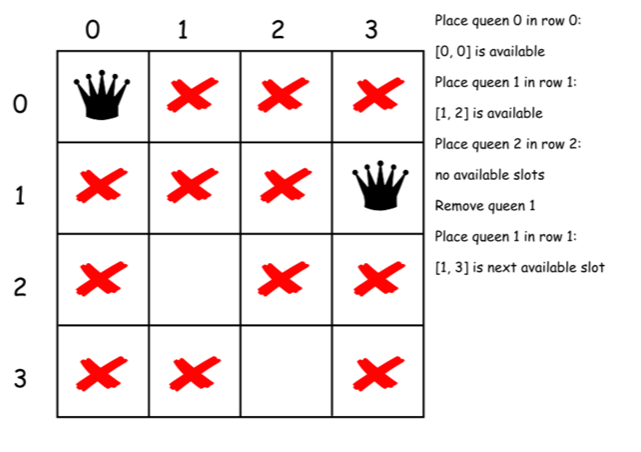
    • Else
      • 继续考虑接下来的皇后放置 backtrack(row + 1).
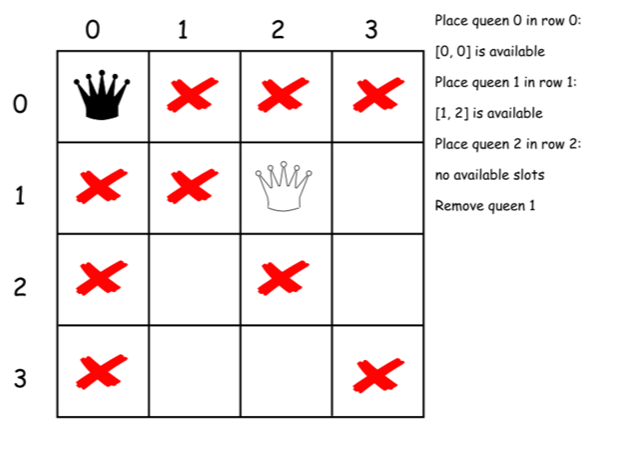
    • 回溯：将在 (row, column) 方格的皇后移除.

下面是上述算法的一个直接的实现。

1 / 34

• Java
• Python

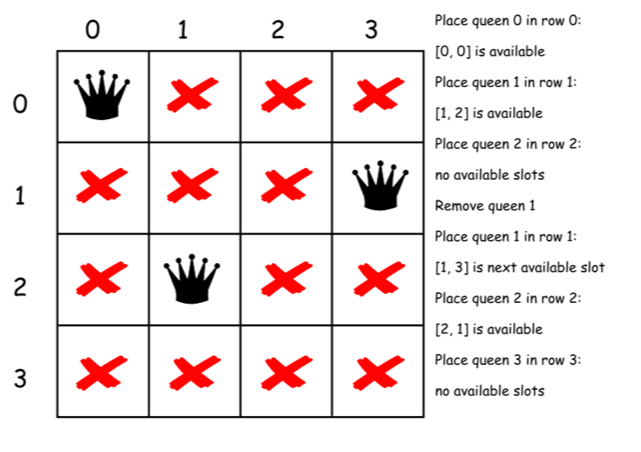
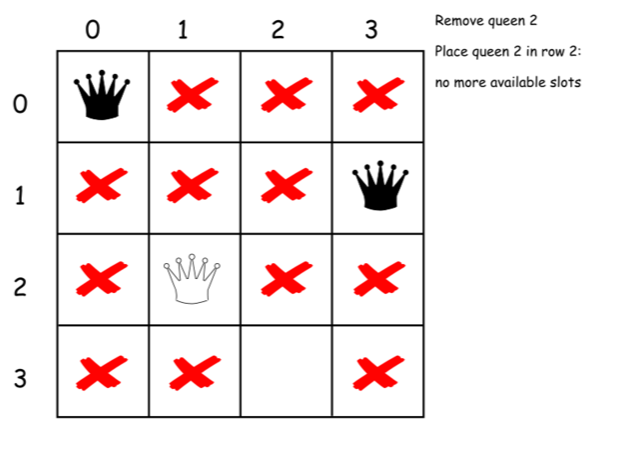
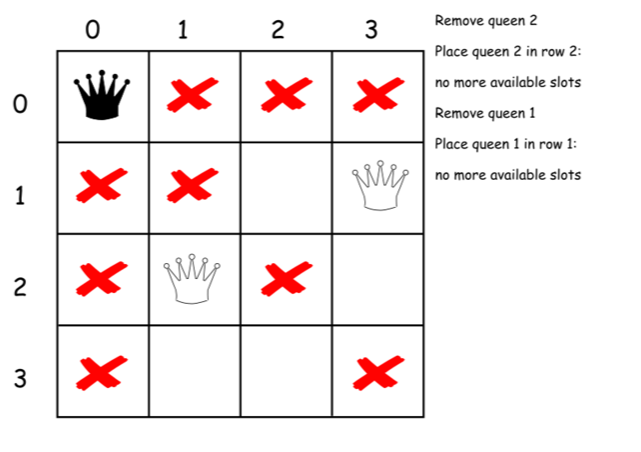
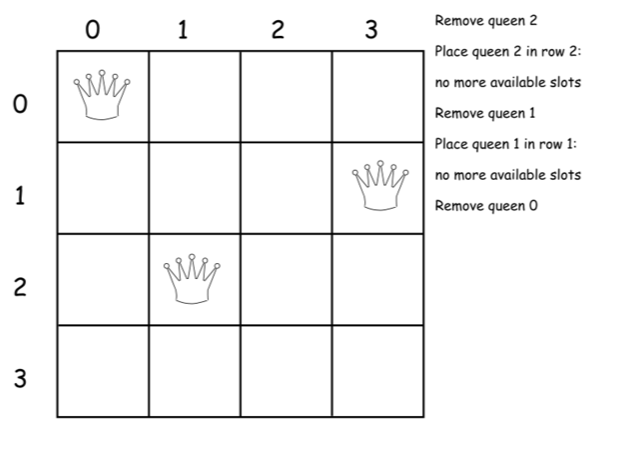
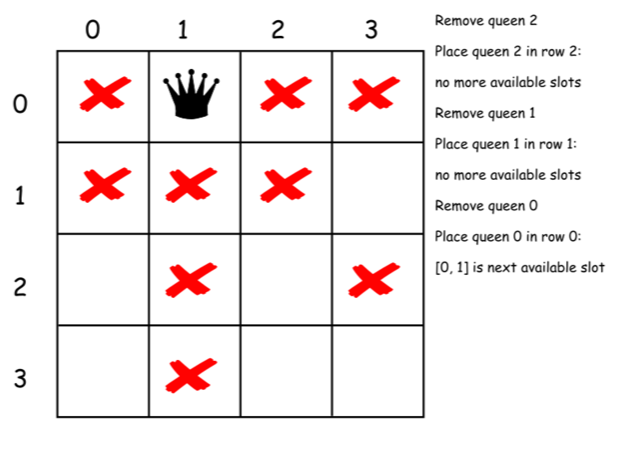
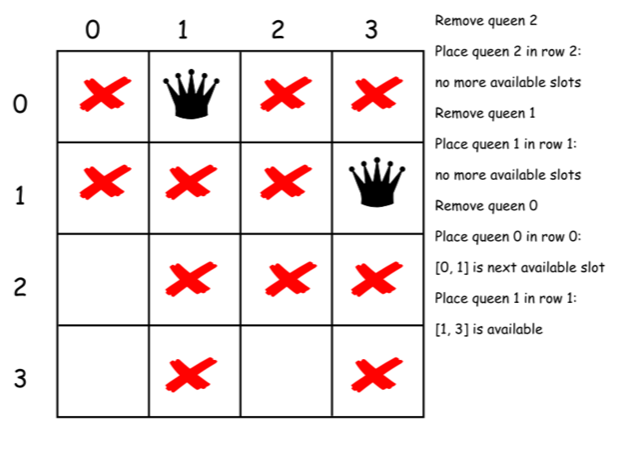
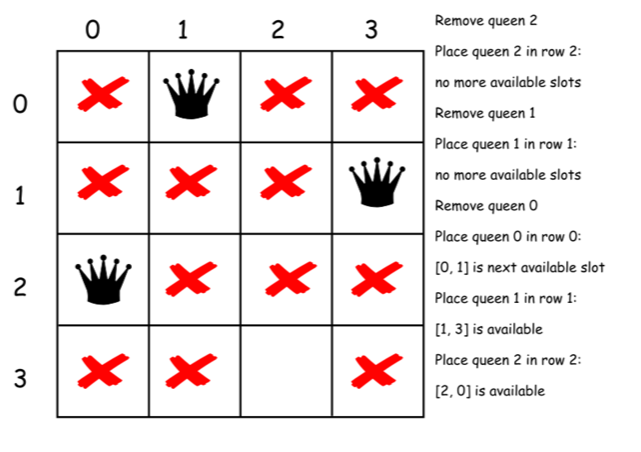
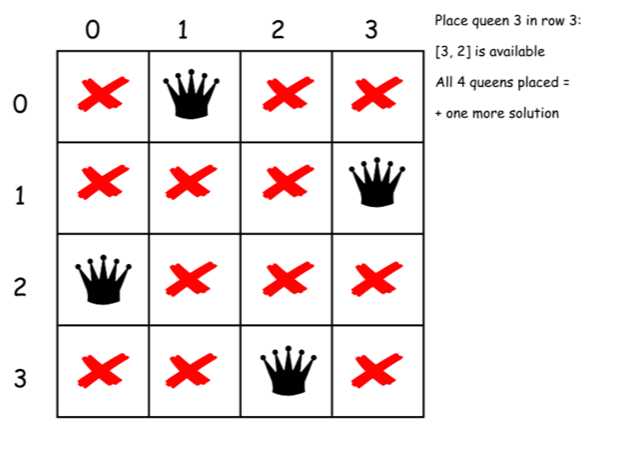
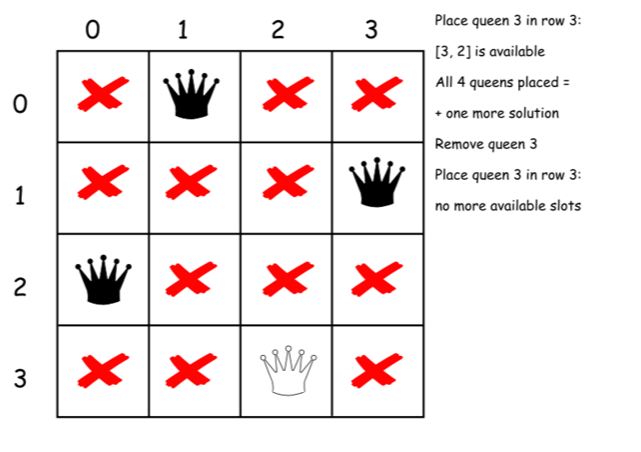
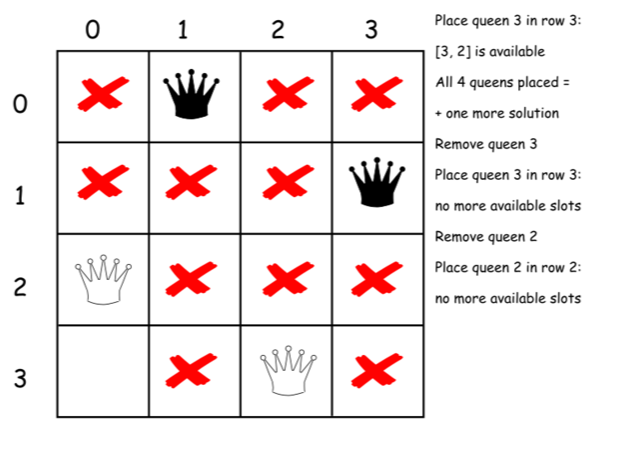
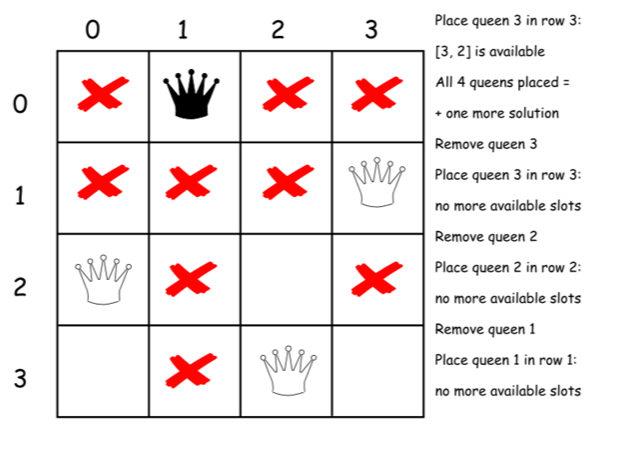
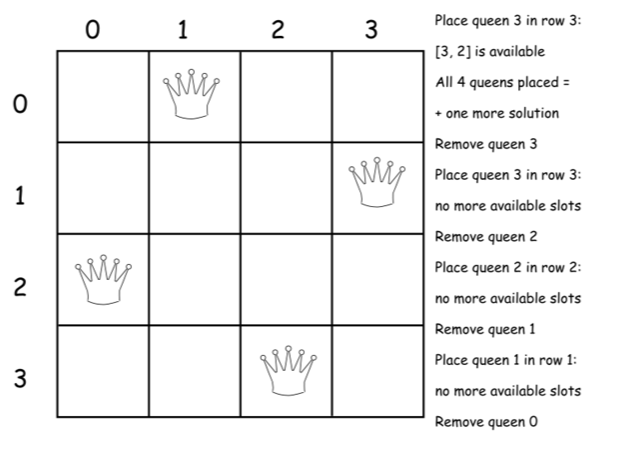
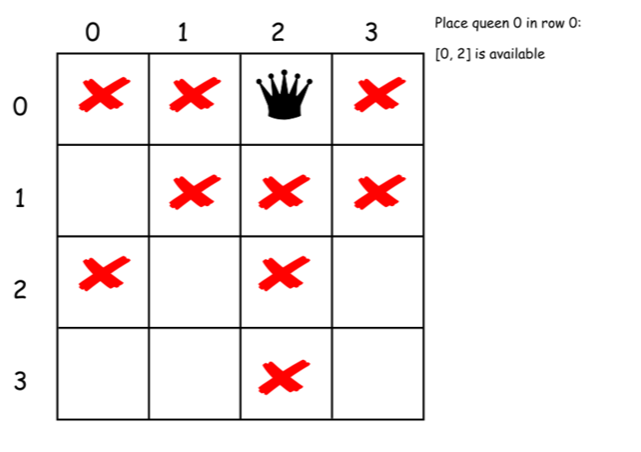
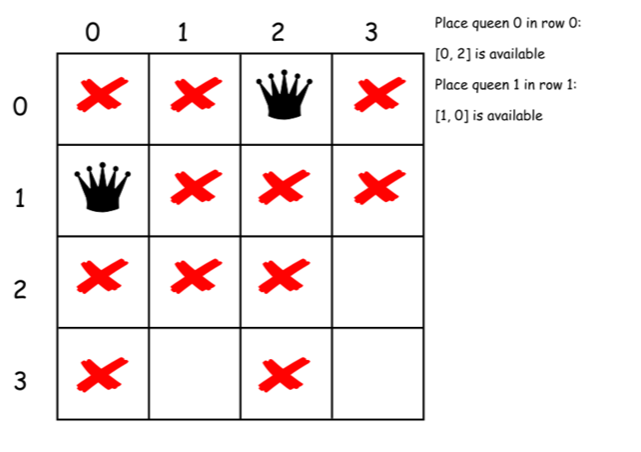
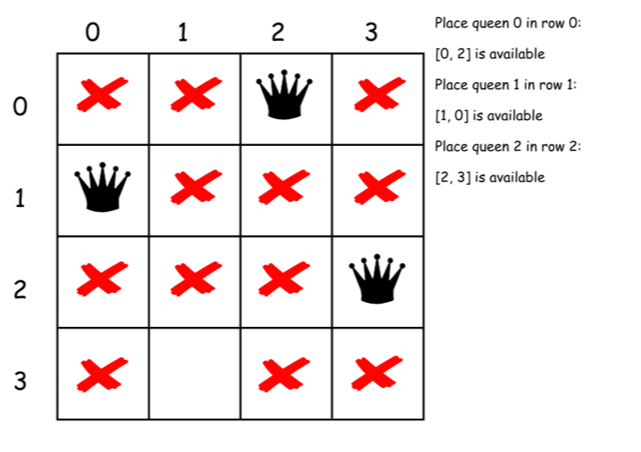
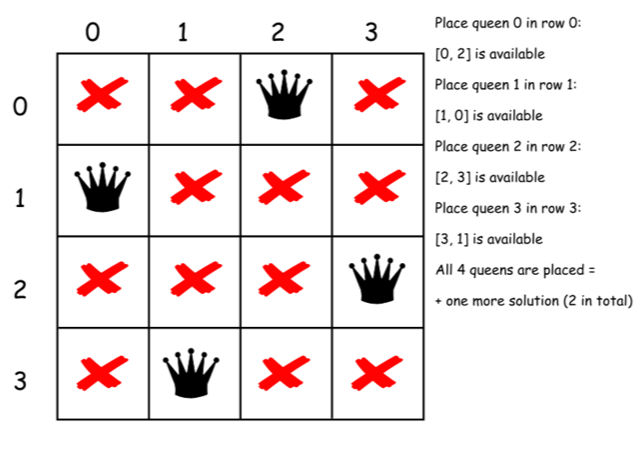
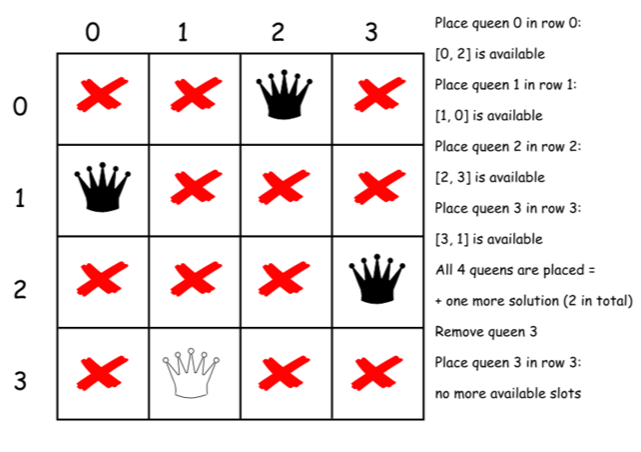
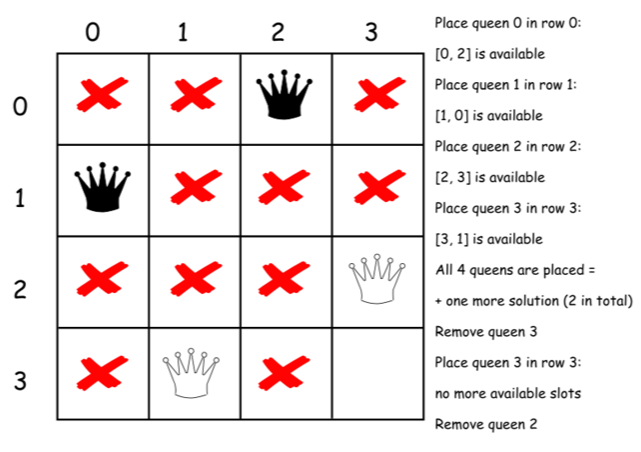
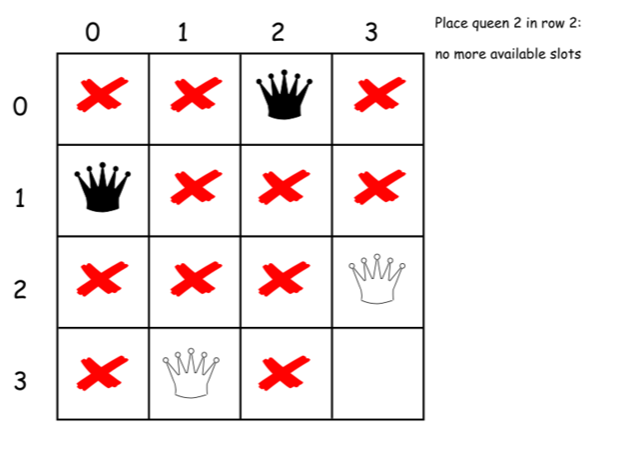
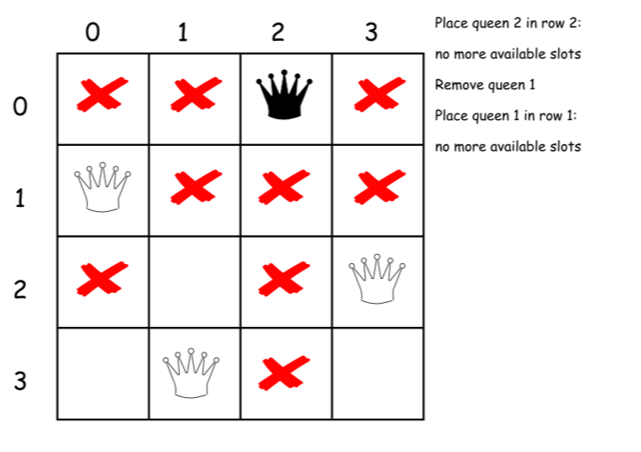
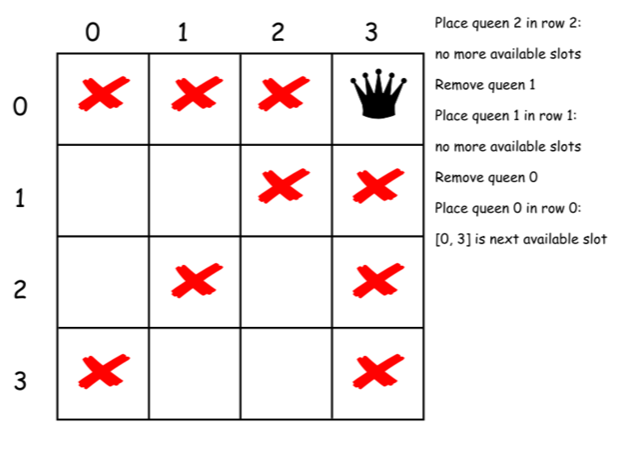
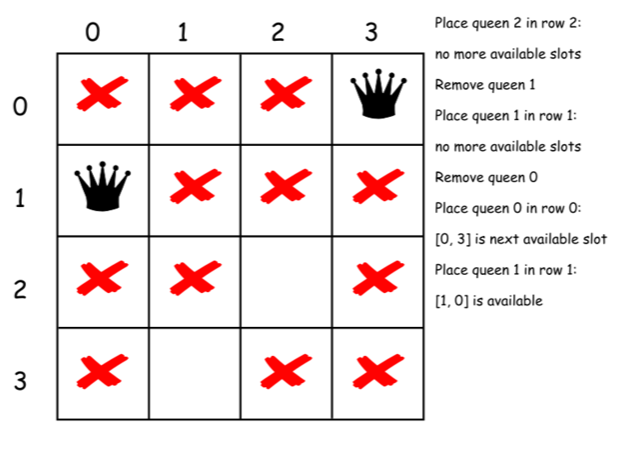
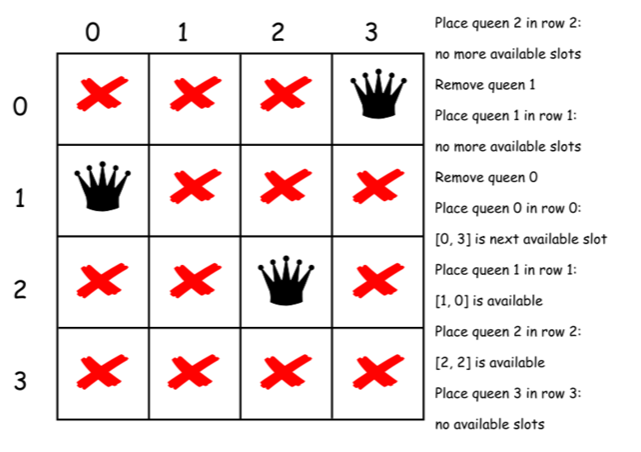
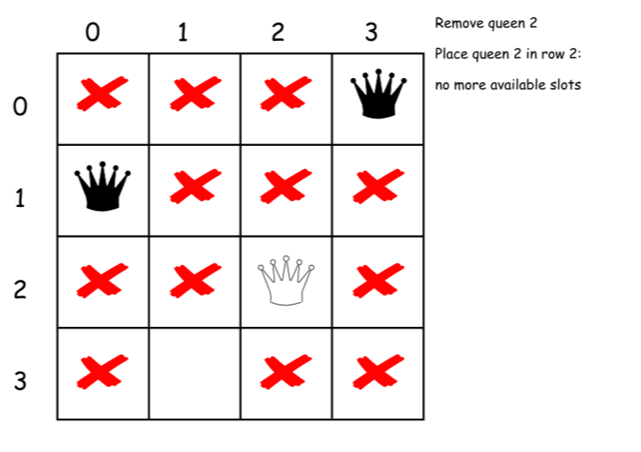
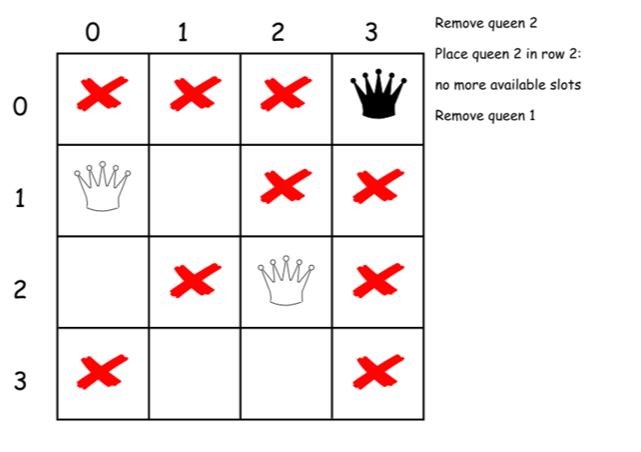
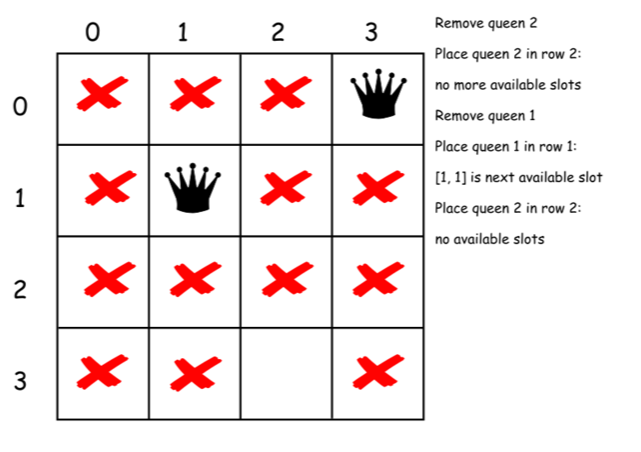
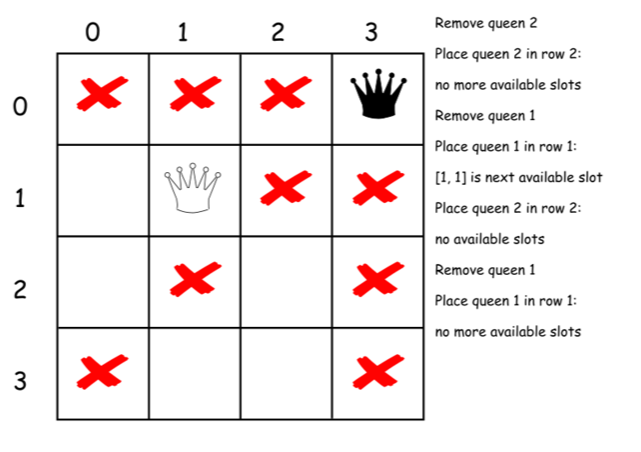
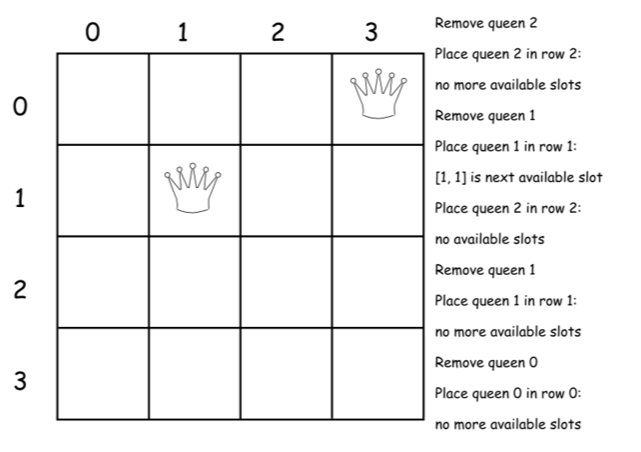
class Solution {
  int rows[];
  // "hill" diagonals
  int hills[];
  // "dale" diagonals
  int dales[];
  int n;
  // output
  List<List<String>> output = new ArrayList();
  // queens positions
  int queens[];
public boolean isNotUnderAttack(int row, int col) {

int res = rows[col] + hills[row - col + 2 * n] + dales[row + col];

return (res == 0) ? true : false;

}
public void placeQueen(int row, int col) {

queens[row] = col;

rows[col] = 1;

hills[row - col + 2 * n] = 1;  // "hill" diagonals

dales[row + col] = 1;   //"dale" diagonals

}
public void removeQueen(int row, int col) {

queens[row] = 0;

rows[col] = 0;

hills[row - col + 2 * n] = 0;

dales[row + col] = 0;

}
public void addSolution() {

List<String> solution = new ArrayList<String>();

for (int i = 0; i < n; ++i) {

int col = queens[i];

StringBuilder sb = new StringBuilder();

for(int j = 0; j < col; ++j) sb.append(".");

sb.append("Q");

for(int j = 0; j < n - col - 1; ++j) sb.append(".");

solution.add(sb.toString());

}

output.add(solution);

}
public void backtrack(int row) {

for (int col = 0; col < n; col++) {

if (isNotUnderAttack(row, col)) {

placeQueen(row, col);

// if n queens are already placed

if (row + 1 == n) addSolution();

// if not proceed to place the rest

else backtrack(row + 1);

// backtrack

removeQueen(row, col);

}

}

}
public List<List<String>> solveNQueens(int n) {

this.n = n;

rows = new int[n];

hills = new int[4 * n - 1];

dales = new int[2 * n - 1];

queens = new int[n];
backtrack(<span class="hljs-number">0</span>);
<span class="hljs-keyword">return</span> output;

}

}

class Solution:

def solveNQueens(self, n: int) -> List[List[str]]:

def could_place(row, col):

return not (cols[col] + hill_diagonals[row - col] + dale_diagonals[row + col])

    <span class="hljs-function"><span class="hljs-keyword">def</span> <span class="hljs-title">place_queen</span><span class="hljs-params">(row, col)</span>:</span>
        queens.add((row, col))
        cols[col] = <span class="hljs-number">1</span>
        hill_diagonals[row - col] = <span class="hljs-number">1</span>
        dale_diagonals[row + col] = <span class="hljs-number">1</span>
    
    <span class="hljs-function"><span class="hljs-keyword">def</span> <span class="hljs-title">remove_queen</span><span class="hljs-params">(row, col)</span>:</span>
        queens.remove((row, col))
        cols[col] = <span class="hljs-number">0</span>
        hill_diagonals[row - col] = <span class="hljs-number">0</span>
        dale_diagonals[row + col] = <span class="hljs-number">0</span>
    
    <span class="hljs-function"><span class="hljs-keyword">def</span> <span class="hljs-title">add_solution</span><span class="hljs-params">()</span>:</span>
        solution = []
        <span class="hljs-keyword">for</span> _, col <span class="hljs-keyword">in</span> sorted(queens):
            solution.append(<span class="hljs-string">'.'</span> * col + <span class="hljs-string">'Q'</span> + <span class="hljs-string">'.'</span> * (n - col - <span class="hljs-number">1</span>))
        output.append(solution)
    
    <span class="hljs-function"><span class="hljs-keyword">def</span> <span class="hljs-title">backtrack</span><span class="hljs-params">(row = <span class="hljs-number">0</span>)</span>:</span>
        <span class="hljs-keyword">for</span> col <span class="hljs-keyword">in</span> range(n):
            <span class="hljs-keyword">if</span> could_place(row, col):
                place_queen(row, col)
                <span class="hljs-keyword">if</span> row + <span class="hljs-number">1</span> == n:
                    add_solution()
                <span class="hljs-keyword">else</span>:
                    backtrack(row + <span class="hljs-number">1</span>)
                remove_queen(row, col)
    
    cols = [<span class="hljs-number">0</span>] * n
    hill_diagonals = [<span class="hljs-number">0</span>] * (<span class="hljs-number">2</span> * n - <span class="hljs-number">1</span>)
    dale_diagonals = [<span class="hljs-number">0</span>] * (<span class="hljs-number">2</span> * n - <span class="hljs-number">1</span>)
    queens = set()
    output = []
    backtrack()
    <span class="hljs-keyword">return</span> output

复杂度分析

• 时间复杂度：$\mathcal{O}(N!)$. 放置第 1 个皇后有 N 种可能的方法，放置两个皇后的方法不超过 N (N - 2) ，放置 3 个皇后的方法不超过 N(N - 2)(N - 4) ，以此类推。总体上，时间复杂度为 $\mathcal{O}(N!)$ .
• 空间复杂度：$\mathcal{O}(N)$ . 需要保存对角线和行的信息。