leetcode题解之47. 全排列 II

给定一个可包含重复数字的序列，返回所有不重复的全排列。

示例:

[https://www.jianshu.com/p/7a71c9ea42df](https://www.jianshu.com/p/7a71c9ea42df)

输入: [1,1,2]
输出:
[
  [1,1,2],
  [1,2,1],
  [2,1,1]
]

刷新重试诊断

code：

vid:

uuid:

requestId:

播放时间：

提示信息

字幕

倍速

清晰度

音轨

倍速正常

字幕Off

音轨

清晰度

00:00 / 04:42

确认取消

这一题是在「力扣」第 46 题： “全排列” 的基础上增加了“序列中的元素可重复”这一条件，但要求返回的结果又不能有重复元素。

思路：在一定会产生重复结果集的地方剪枝。

一个比较容易想到的办法是在结果集中去重。但是问题又来了，这些结果集的元素是一个又一个列表，对列表去重不像用哈希表对基本元素去重那样容易。

如果要比较两个列表是否一样，一个很显然的办法是分别排序，然后逐个比对。既然要排序，我们可以在搜索之前就对候选数组排序，一旦发现这一支搜索下去可能搜索到重复的元素就停止搜索，这样结果集中不会包含重复元素。

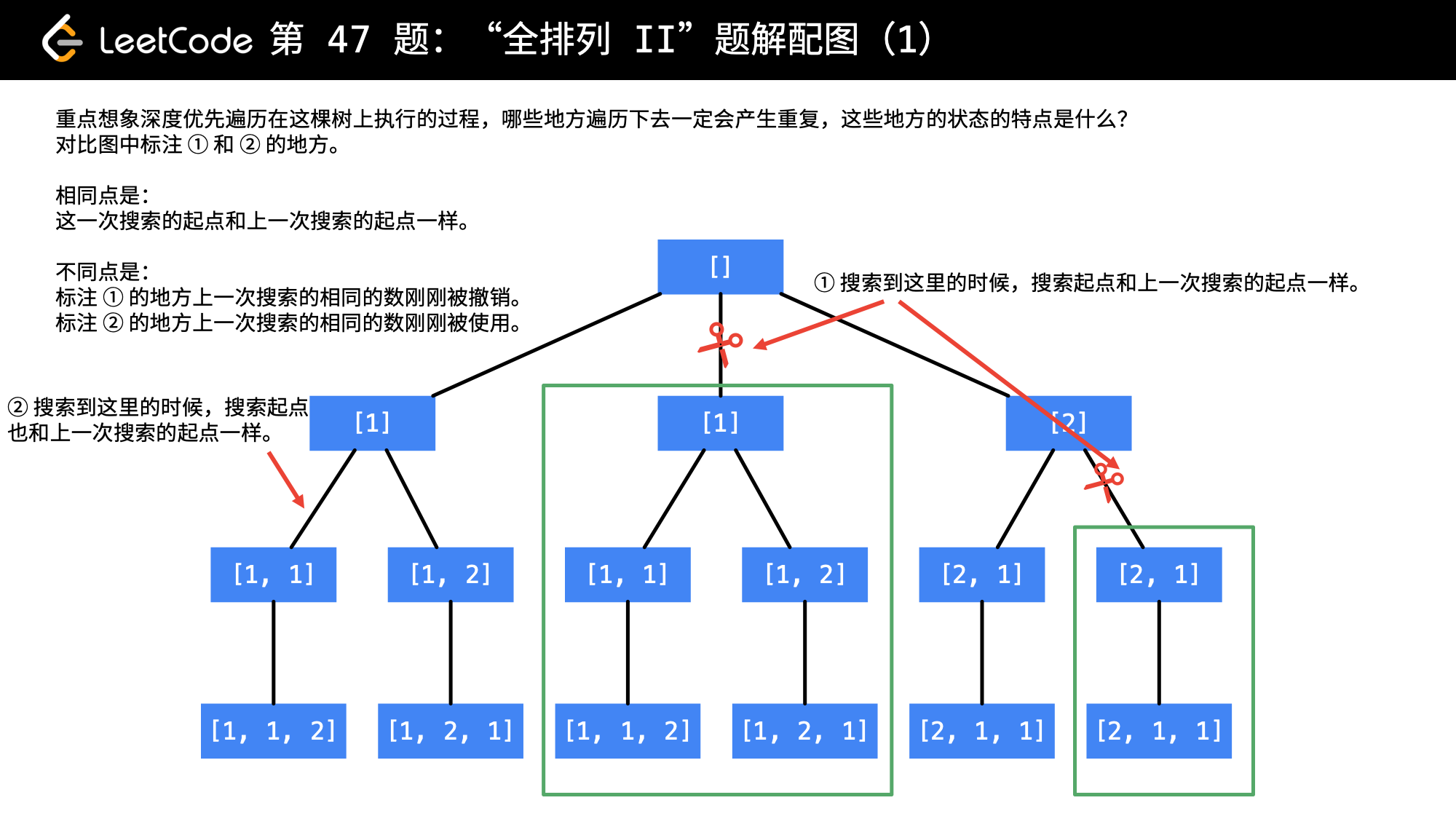
产生重复结点的地方，正是图中标注了“剪刀”，且被绿色框框住的地方。

大家也可以把第 2 个 1 加上 ' ，即 [1, 1', 2] 去想象这个搜索的过程。只要遇到起点一样，就有可能产生重复。这里还有一个很细节的地方：

1、在图中 ② 处，搜索的数也和上一次一样，但是上一次的 1 还在使用中；
2、在图中 ① 处，搜索的数也和上一次一样，但是上一次的 1 刚刚被撤销，正是因为刚被撤销，下面的搜索中还会使用到，因此会产生重复，剪掉的就应该是这样的分支。

代码实现方面，在第 46 题的基础上，要加上这样一段代码：

• Java

if (i > 0 && nums[i] == nums[i - 1] && !used[i - 1]) {
    continue;
}

这段代码就能检测到标注为 ① 的两个结点，跳过它们。注意：这里 used[i - 1] 不加 !，测评也能通过。有兴趣的朋友可以想一想这是为什么。建议大家做这样几个对比实验：

1、干脆就不写 !used[i - 1] 结果是什么样？
2、写 used[i - 1] 结果是什么，代码又是怎样执行的。这里给的结论是：!used[i - 1] 这样的剪枝更彻底。附录会分析原因。

参考代码 1：

• Java
• Python

import java.util.ArrayDeque;
import java.util.ArrayList;
import java.util.Arrays;
import java.util.Deque;
import java.util.List;
public class Solution {
<span class="hljs-keyword">public</span> List&lt;List&lt;Integer&gt;&gt; permuteUnique(<span class="hljs-keyword">int</span>[] nums) {
    <span class="hljs-keyword">int</span> len = nums.length;
    List&lt;List&lt;Integer&gt;&gt; res = <span class="hljs-keyword">new</span> ArrayList&lt;&gt;();
    <span class="hljs-keyword">if</span> (len == <span class="hljs-number">0</span>) {
        <span class="hljs-keyword">return</span> res;
    }

    <span class="hljs-comment">// 排序（升序或者降序都可以），排序是剪枝的前提</span>
    Arrays.sort(nums);

    <span class="hljs-keyword">boolean</span>[] used = <span class="hljs-keyword">new</span> <span class="hljs-keyword">boolean</span>[len];
    <span class="hljs-comment">// 使用 Deque 是 Java 官方 Stack 类的建议</span>
    Deque&lt;Integer&gt; path = <span class="hljs-keyword">new</span> ArrayDeque&lt;&gt;(len);
    dfs(nums, len, <span class="hljs-number">0</span>, used, path, res);
    <span class="hljs-keyword">return</span> res;
}

<span class="hljs-function"><span class="hljs-keyword">private</span> <span class="hljs-keyword">void</span> <span class="hljs-title">dfs</span><span class="hljs-params">(<span class="hljs-keyword">int</span>[] nums, <span class="hljs-keyword">int</span> len, <span class="hljs-keyword">int</span> depth, <span class="hljs-keyword">boolean</span>[] used, Deque&lt;Integer&gt; path, List&lt;List&lt;Integer&gt;&gt; res)</span> </span>{
    <span class="hljs-keyword">if</span> (depth == len) {
        res.add(<span class="hljs-keyword">new</span> ArrayList&lt;&gt;(path));
        <span class="hljs-keyword">return</span>;
    }

    <span class="hljs-keyword">for</span> (<span class="hljs-keyword">int</span> i = <span class="hljs-number">0</span>; i &lt; len; ++i) {
        <span class="hljs-keyword">if</span> (used[i]) {
            <span class="hljs-keyword">continue</span>;
        }

        <span class="hljs-comment">// 剪枝条件：i &gt; 0 是为了保证 nums[i - 1] 有意义</span>
        <span class="hljs-comment">// 写 !used[i - 1] 是因为 nums[i - 1] 在深度优先遍历的过程中刚刚被撤销选择</span>
        <span class="hljs-keyword">if</span> (i &gt; <span class="hljs-number">0</span> &amp;&amp; nums[i] == nums[i - <span class="hljs-number">1</span>] &amp;&amp; !used[i - <span class="hljs-number">1</span>]) {
            <span class="hljs-keyword">continue</span>;
        }

        path.addLast(nums[i]);
        used[i] = <span class="hljs-keyword">true</span>;

        dfs(nums, len, depth + <span class="hljs-number">1</span>, used, path, res);
        <span class="hljs-comment">// 回溯部分的代码，和 dfs 之前的代码是对称的</span>
        used[i] = <span class="hljs-keyword">false</span>;
        path.removeLast();
    }
}

<span class="hljs-function"><span class="hljs-keyword">public</span> <span class="hljs-keyword">static</span> <span class="hljs-keyword">void</span> <span class="hljs-title">main</span><span class="hljs-params">(String[] args)</span> </span>{
    Solution solution = <span class="hljs-keyword">new</span> Solution();
    <span class="hljs-keyword">int</span>[] nums = {<span class="hljs-number">1</span>, <span class="hljs-number">1</span>, <span class="hljs-number">2</span>};
    List&lt;List&lt;Integer&gt;&gt; res = solution.permuteUnique(nums);
    System.out.println(res);
}

}

from typing import List

class Solution:
<span class="hljs-function"><span class="hljs-keyword">def</span> <span class="hljs-title">permuteUnique</span><span class="hljs-params">(self, nums: List[int])</span> -&gt; List[List[int]]:</span>

    <span class="hljs-function"><span class="hljs-keyword">def</span> <span class="hljs-title">dfs</span><span class="hljs-params">(nums, size, depth, path, used, res)</span>:</span>
        <span class="hljs-keyword">if</span> depth == size:
            res.append(path.copy())
            <span class="hljs-keyword">return</span>
        <span class="hljs-keyword">for</span> i <span class="hljs-keyword">in</span> range(size):
            <span class="hljs-keyword">if</span> <span class="hljs-keyword">not</span> used[i]:

                <span class="hljs-keyword">if</span> i &gt; <span class="hljs-number">0</span> <span class="hljs-keyword">and</span> nums[i] == nums[i - <span class="hljs-number">1</span>] <span class="hljs-keyword">and</span> <span class="hljs-keyword">not</span> used[i - <span class="hljs-number">1</span>]:
                    <span class="hljs-keyword">continue</span>

                used[i] = <span class="hljs-literal">True</span>
                path.append(nums[i])
                dfs(nums, size, depth + <span class="hljs-number">1</span>, path, used, res)
                used[i] = <span class="hljs-literal">False</span>
                path.pop()

    size = len(nums)
    <span class="hljs-keyword">if</span> size == <span class="hljs-number">0</span>:
        <span class="hljs-keyword">return</span> []

    nums.sort()

    used = [<span class="hljs-literal">False</span>] * len(nums)
    res = []
    dfs(nums, size, <span class="hljs-number">0</span>, [], used, res)
    <span class="hljs-keyword">return</span> res

复杂度分析：（理由同第 46 题，重复元素越多，剪枝越多。但是计算复杂度的时候需要考虑最差情况。）

• 时间复杂度：$O(N \times N!)$，这里 $N$ 为数组的长度。
• 空间复杂度：$O(N \times N!)$。
  
  

---

补充说明（这部分内容不太重要，只要理解上面深搜是怎么剪枝的就行）

写 used[i - 1] 代码正确，但是不推荐的原因。

思路是根据深度优先遍历的执行流程，看一看那些状态变量（布尔数组 used）的值。

1、如果剪枝写的是：

• Java

if (i > 0 && nums[i] == nums[i - 1] && !used[i - 1]) {
    continue;
}

那么，对于数组 [1, 1’, 1’’, 2]，回溯的过程如下：

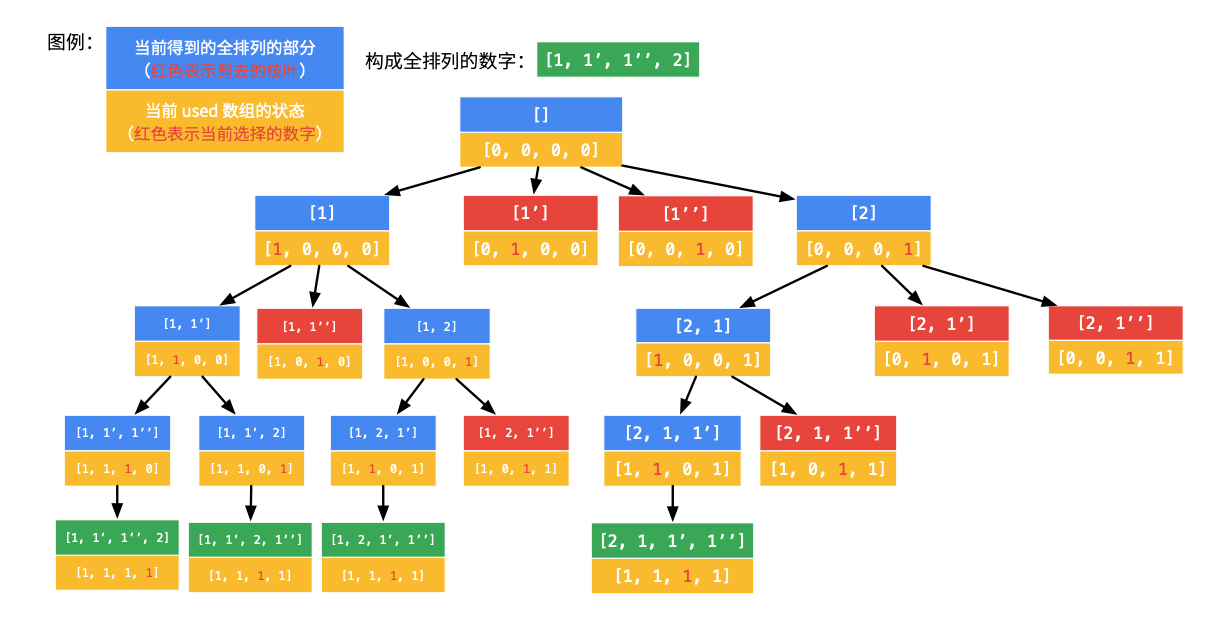
得到的全排列是：[[1, 1', 1'', 2], [1, 1', 2, 1''], [1, 2, 1', 1''], [2, 1, 1', 1'']]。特点是：1、1'、1'' 出现的顺序只能是 1、1'、1''。

2、如果剪枝写的是：

• Java

if (i > 0 && nums[i] == nums[i - 1] && used[i - 1]) {
    continue;
}

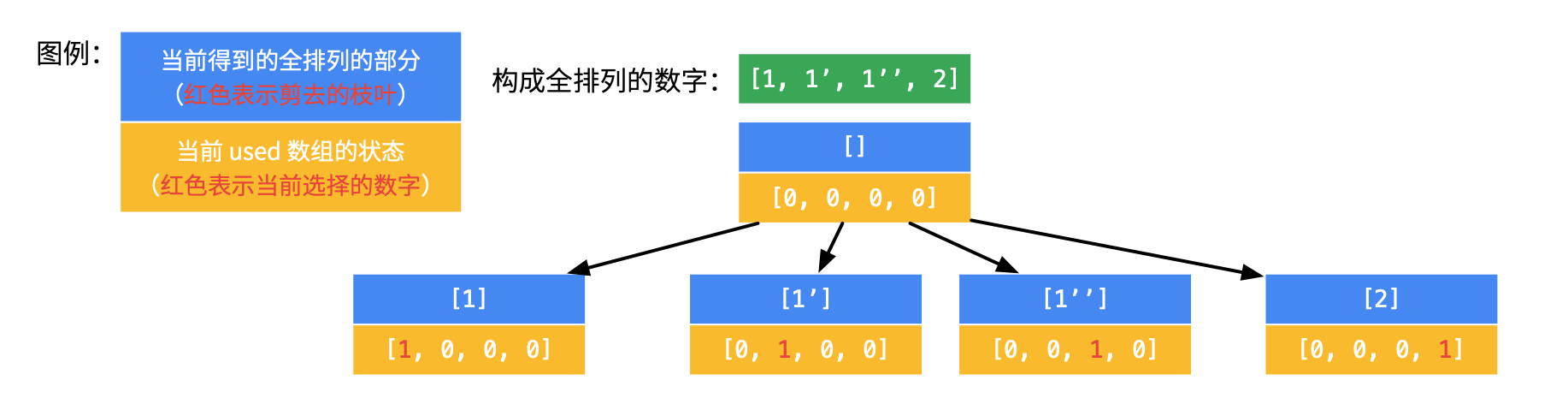
那么，对于数组 [1, 1’, 1’’, 2]，回溯的过程如下（因为过程稍显繁琐，所以没有画在一张图里）：

（1）先选第 1 个数字，有 4 种取法。

（2）对第 1 步的第 1 个分支，可以继续搜索，但是发现，没有搜索到合适的叶子结点。

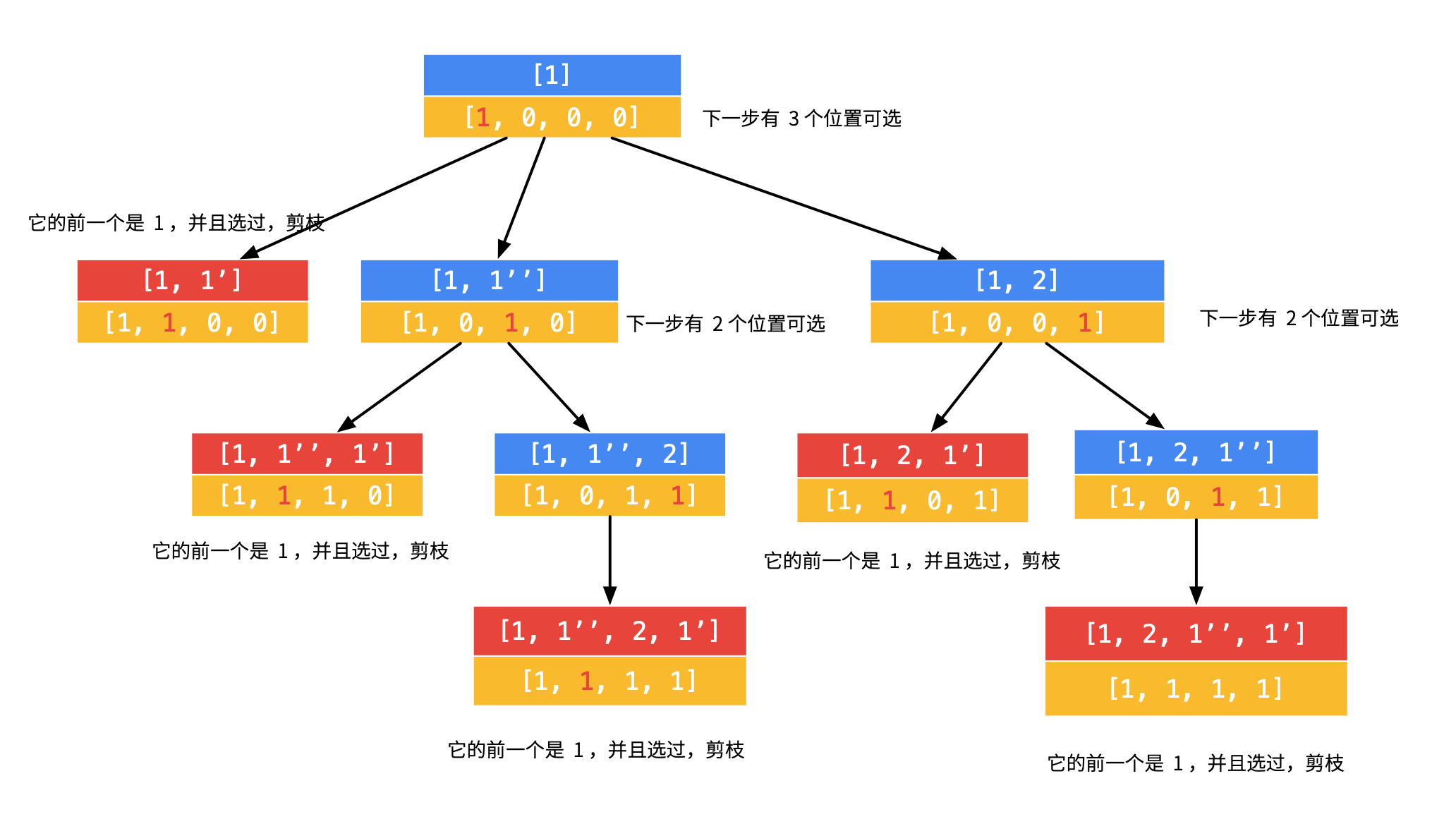
（3）对第 1 步的第 2 个分支，可以继续搜索，但是同样发现，没有搜索到合适的叶子结点。

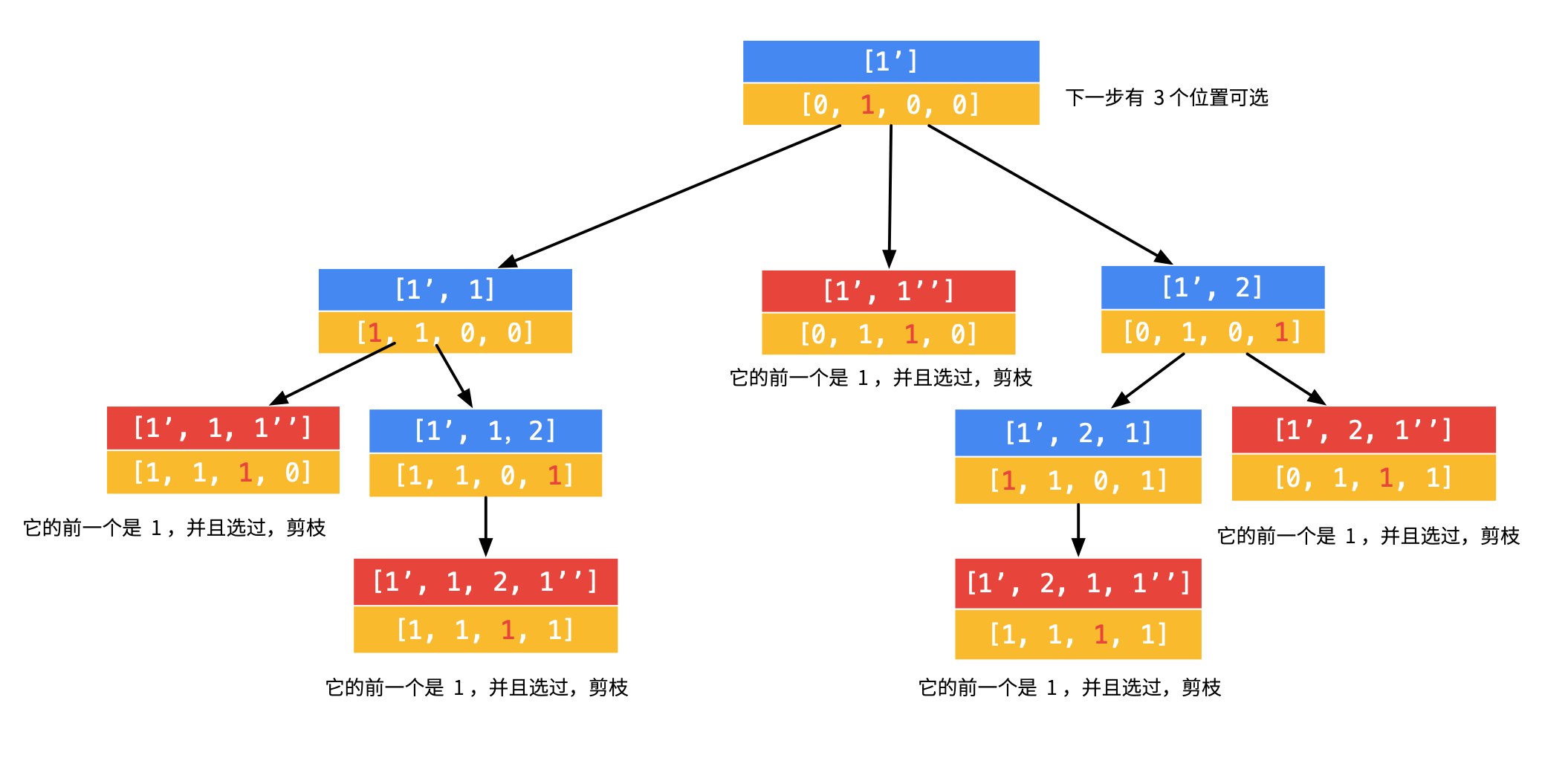
（4）对第 1 步的第 3 个分支，继续搜索发现搜索到合适的叶子结点。

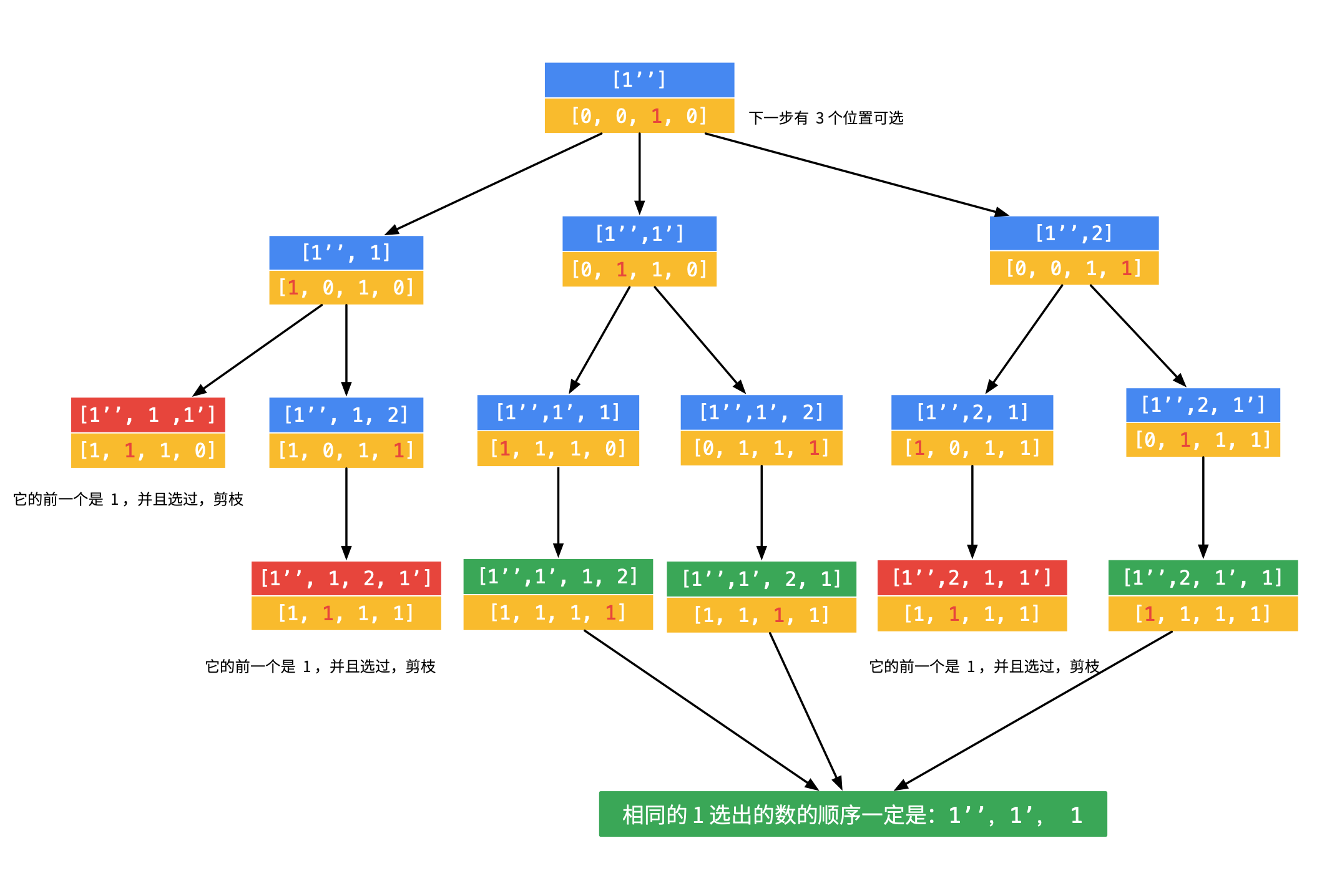
（5）对第 1 步的第 4 个分支，继续搜索发现搜索到合适的叶子结点。

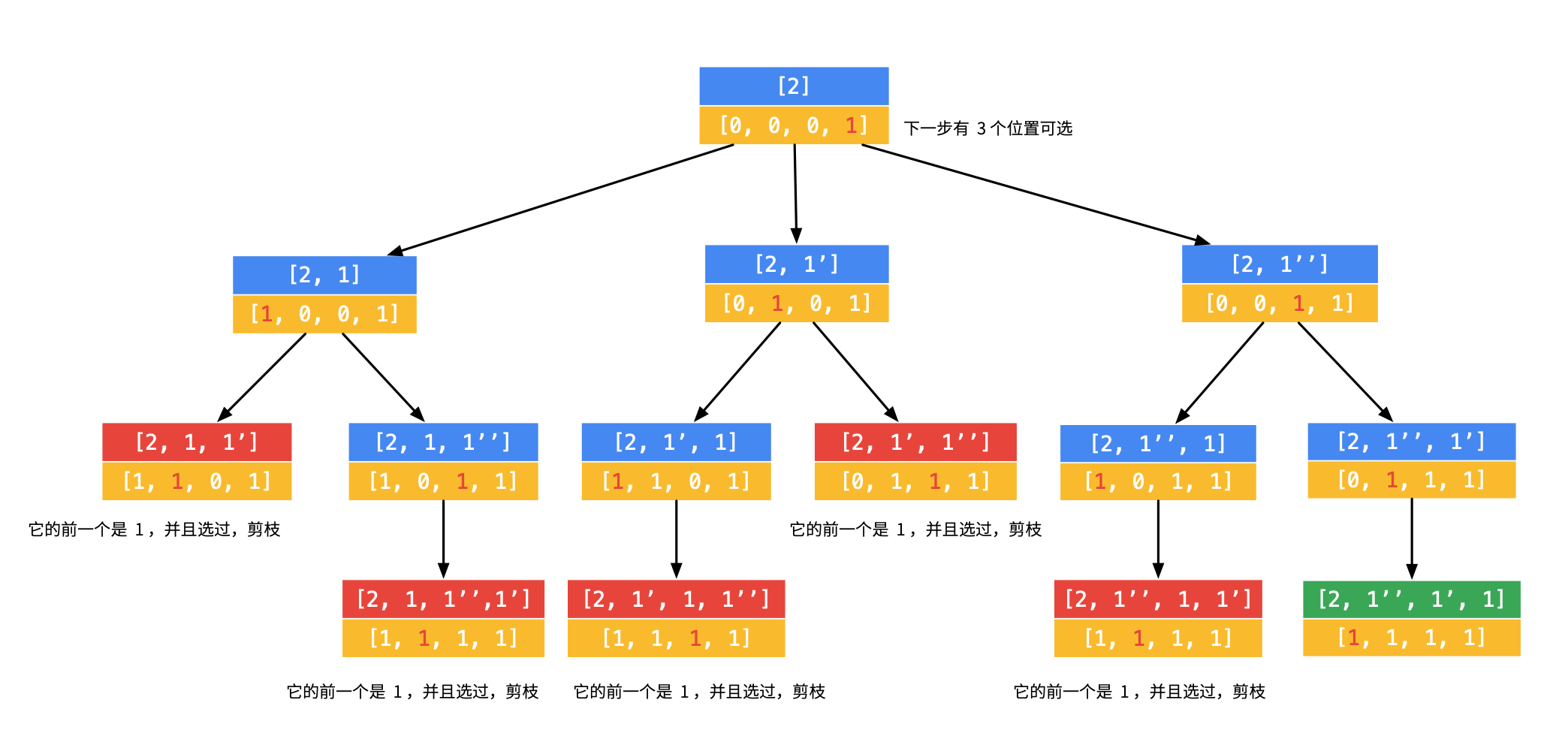
因此，used[i - 1] 前面加不加感叹号的区别仅在于保留的是相同元素的顺序索引，还是倒序索引。很明显，顺序索引（即使用 !used[i - 1] 作为剪枝判定条件得到）的递归树剪枝更彻底，思路也相对较自然。