公路堵车概率模型Python（Nagel-Schreckenberg交通流模型）

　　路面上有N辆车，以不同速度向前行驶，模拟堵车问题。有以下假设：

• 假设某辆车的当前速度是 v
• 如果 前方可见范围内没车，下一秒车速提高到 v+1
• 如果 前方有车，前车的距离为 d ，且 d < v ，则 下一秒车速降低到 d - 1
• 每辆车会以概率 p 随机减速 v - 1 

　　Python代码如下：

import numpy as np
import matplotlib as mpl
import matplotlib.pyplot as plt

def clip(x, path):
    for i in range(len(x)):
        if x[i] >= path:
            x[i] %= path

if __name__ == "__main__":
    # 输出中文（黑体SinHei），仿宋（fangsong）
    mpl.rcParams['font.sans-serif'] = ['SimHei']
    mpl.rcParams['axes.unicode_minus'] = False

    path = 5000     # 环形公路长度
    n = 100         # 公路中的车辆数目
    v0 = 50         # 车辆的初始速度
    p = 0.3         # 随机减速概率
    Times = 3000    # 模拟次数3000

    np.random.seed(0)   # 种子设为0 -> 生成的随机数都相同
    x = np.random.rand(n)*path  # 列表x生成100*5000个随机数
    x.sort()    # 对x升序排序
    v = np.tile([v0], n).astype(float)   # 将v0重复n次并转换为浮点型赋给数组v中的n个元素

    plt.figure(figsize=(9, 7), facecolor='w')   # 创建图像高9英寸宽7英寸，背景色：white = #FFFFFF
    for t in range(Times):  # 每一次是图中的一行数据
        # 测试4行数据
        # if t not in [100, 150, 175, 1000]:
        #     continue
        plt.scatter(x, [t]*n, s=1, c='k', alpha=0.05)   # 横轴x,纵轴t*n(t从0到2999,n=100)
        for i in range(n):  # 对于每一行数据
            # 本车当前速度为v
            # 如果 前方有车 && 前车的距离d < 车速v：下一秒车速 = d-1
            # 如果 没车：加速到 v+1
            # 每辆车以概率p随机减速v-1
            if x[(i+1) % n] > x[i]:
                d = x[(i+1) % n] - x[i]     # 距离前车的距离
            else:
                d = path - x[i] + x[(i+1) % n]
            if v[i] < d:
                if np.random.rand() > p:
                    v[i] += 1
                else:
                    v[i] -= 1
            else:
                v[i] = d - 1
        v = v.clip(0, 150)  # 保证车速是正向的，在0-150之间
        x += v # 位移就是一秒钟时间的速度，速度v之和就是位移x
        clip(x, path)
    plt.xlim(0, path)       # x的取值范围x limit=0-5000
    plt.ylim(0, Times)
    plt.xlabel('车辆位置', fontsize=14)
    plt.ylabel('模拟时间', fontsize=14)
    plt.title('环形公路车辆堵车模拟', fontsize=18)
    plt.tight_layout(pad=2)     # pad越小，坐标轴越靠边
    # plt.savefig('环形公路车辆堵车模拟.png')
    plt.show()

　　　　结果：

　　

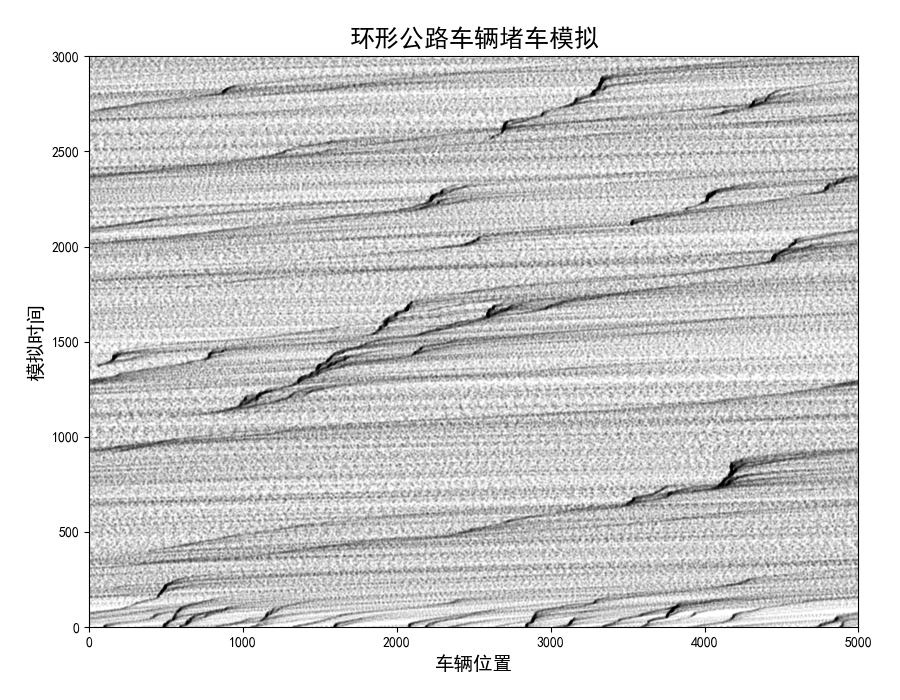
　　　　以上为本人在b站听了邹博老师陆家嘴学堂视频课之后的结果。