基于MATLAB边缘检测算子的实现
基于MATLAB边缘检测算子的实现
作者:lee神
- 1. 概述
边缘检测是图像处理和计算机视觉中的基本问题,边缘检测的目的是标识数字图像中亮度变化明显的点。图像属性中的显著变化通常反映了属性的重要事件和变化。 这些包括(i)深度上的不连续、(ii)表面方向不连续、(iii)物质属性变化和(iv)场景照明变化。 边缘检测是图像处理和计算机视觉中,尤其是特征提取中的一个研究领域。
一阶: Roberts Cross算子,Prewitt算子,Sobel算子, Kirsch算子,罗盘算子;
二阶: Marr-Hildreth,在梯度方向的二阶导数过零点,Canny算子,Laplacian算子。
- 2. 经典边缘检测算子的简介
Roberts算子,又称罗伯茨算子,是一种最简单的算子,是一种利用局部差分算子寻找边缘的算子。他采用对角线方向相邻两象素之差近似梯度幅值检测边缘。检测垂直边缘的效果好于斜向边缘,定位精度高,对噪声敏感,无法抑制噪声的影响。
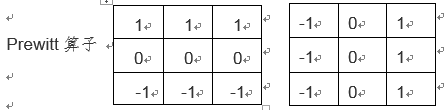
Prewitt算子是一种一阶微分算子的边缘检测,利用像素点上下、左右邻点的灰度差,在边缘处达到极值检测边缘,去掉部分伪边缘,对噪声具有平滑作用 。其原理是在图像空间利用两个方向模板与图像进行邻域卷积来完成的,这两个方向模板一个检测水平边缘,一个检测垂直边缘。
对数字图像f(x,y),Prewitt算子的定义如下:
G(i)={[f(i-1,j-1)+f(i-1,j)+f(i-1,j+1)]-[f(i+1,j-1)+f(i+1,j)+f(i+1,j+1)]}
G(j)={[f(i-1,j+1)+f(i,j+1)+f(i+1,j+1)]-[f(i-1,j-1)+f(i,j-1)+f(i+1,j-1)]}
则 P(i,j)=max[G(i),G(j)]或 P(i,j)=G(i)+G(j)
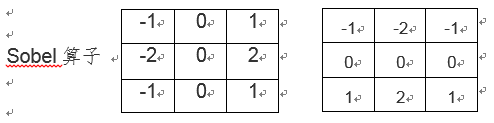
Sobel算法是像素图像边缘检测中最重要的算子之一,在机器学习、数字媒体、计算机视觉等信息科技领域起着举足轻重的作用。在技术上,它是一个离散的一阶差分算子,用来计算图像亮度函数的一阶梯度之近似值。在图像的任何一点使用此算子,将会产生该点对应的梯度矢量或是其法矢量。
Laplacian 算子是n维欧几里德空间中的一个二阶微分算子,定义为梯度grad的散度div。可使用运算模板来运算这定理定律。
函数的拉普拉斯算子也是该函数的黑塞矩阵的迹,可以证明,它具有各向同性,即与坐标轴方向无关,坐标轴旋转后梯度结果不变。如果邻域系统是4 邻域,Laplacian 算子的模板为:
|
0 |
1 |
0 |
|
1 |
-4 |
1 |
|
0 |
1 |
0 |
4邻域Laplacian 算子
如果邻域系统是8 邻域,Laplacian 算子的模板为:
|
1 |
1 |
1 |
|
1 |
-8 |
1 |
|
1 |
1 |
1 |
8 邻域Laplacian 算子
前面提过,Laplacian 算子对噪声比较敏感,所以图像一般先经过平滑处理,因为平滑处理也是用模板进行的,所以,通常的分割算法都是把Laplacian 算子和平滑算子结合起来生成一个新的模板。
- 3. MATLAB实现方法一
实验原图:

使用Matlab内部函数edge实现边缘检测算法:
I=imread('lena.jpg');%提取图像
img=rgb2gray(I);
[m,n]=size(img);
BW1=edge(img,'sobel'); %用Sobel算子进行边缘检测
BW2=edge(img,'roberts');%用Roberts算子进行边缘检测
BW3=edge(img,'prewitt'); %用Prewitt算子进行边缘检测
BW4=edge(img,'log'); %用Log算子进行边缘检测
BW5=edge(img,'canny'); %用Canny算子进行边缘检测
h=fspecial('gaussian',5);%¸高斯滤波
BW6=edge(img,'canny');%高斯滤波后使用Canny算子进行边缘检测
subplot(2,3,1), imshow(BW1);
title('sobel edge check');
subplot(2,3,2), imshow(BW2);
title('roberts edge check');
subplot(2,3,3), imshow(BW3);
title('prewitt edge check');
subplot(2,3,4), imshow(BW4);
title('log edge check');
subplot(2,3,5), imshow(BW5);
title('canny edge check');
subplot(2,3,6), imshow(BW6);
title('gasussian&canny edge check');
实现结果:

- 4. 方法二
实验原图

1)Laplacian 算子的实现:
clear;
sourcePic=imread('lena.jpg');%图像读入
grayPic=mat2gray(sourcePic);%实现图像的矩阵归一化操作
[m,n]=size(grayPic);
newGrayPic=grayPic;
LaplacianNum=0;%经Laplacian操作得到的每个像素的值
LaplacianThreshold=0.2;%设定阈值
for j=2:m-1 %进行边界提取
for k=2:n-1
LaplacianNum=abs(4*grayPic(j,k)-grayPic(j-1,k)-grayPic(j+1,k)-grayPic(j,k+1)-grayPic(j,k-1));
if(LaplacianNum > LaplacianThreshold)
newGrayPic(j,k)=255;
else
newGrayPic(j,k)=0;
end
end
end
figure,imshow(newGrayPic);
title('Laplacian算子的处理结果')
实现结果:

2)Prewitt 算子的实现:
clear;
sourcePic=imread('lena.jpg');
grayPic=mat2gray(sourcePic);
[m,n]=size(grayPic);
newGrayPic=grayPic;
PrewittNum=0;
PrewittThreshold=0.5;%设定阈值
for j=2:m-1 %进行边界提取
for k=2:n-1
PrewittNum=abs(grayPic(j-1,k+1)-grayPic(j+1,k+1)+grayPic(j-1,k)-grayPic(j+1,k)+grayPic(j-1,k-1)-grayPic(j+1,k-1))+abs(grayPic(j-1,k+1)+grayPic(j,k+1)+grayPic(j+1,k+1)-grayPic(j-1,k-1)-grayPic(j,k-1)-grayPic(j+1,k-1));
if(PrewittNum > PrewittThreshold)
newGrayPic(j,k)=255;
else
newGrayPic(j,k)=0;
end
end
end
figure,imshow(newGrayPic);
title('Prewitt算子的处理结果')
实现结果:

3)Sobel 算子的实现:
clear;
sourcePic=imread('lena.jpg');
grayPic=mat2gray(sourcePic);
[m,n]=size(grayPic);
newGrayPic=grayPic;
sobelNum=0;
sobelThreshold=0.7;
for j=2:m-1
for k=2:n-1
sobelNum=abs(grayPic(j-1,k+1)+2*grayPic(j,k+1)+grayPic(j+1,k+1)-grayPic(j-1,k-1)-2*grayPic(j,k-1)-grayPic(j+1,k-1))+abs(grayPic(j-1,k-1)+2*grayPic(j-1,k)+grayPic(j-1,k+1)-grayPic(j+1,k-1)-2*grayPic(j+1,k)-grayPic(j+1,k+1));
if(sobelNum > sobelThreshold)
newGrayPic(j,k)=255;
else
newGrayPic(j,k)=0;
end
end
end
figure,imshow(newGrayPic);
title('Sobel算子的处理结果')
实现结果:

5)Roberts 算子的实现:
clear all;
clc;
sourcePic=imread('lena.jpg');
grayPic=mat2gray(sourcePic);
[m,n]=size(grayPic);
newGrayPic=grayPic;
robertsNum=0;
robertThreshold=0.2;
for j=1:m-1
for k=1:n-1
robertsNum = abs(grayPic(j,k)-grayPic(j+1,k+1)) + abs(grayPic(j+1,k)-grayPic(j,k+1));
if(robertsNum > robertThreshold)
newGrayPic(j,k)=255;
else
newGrayPic(j,k)=0;
end
end
end
figure,imshow(newGrayPic);
title('roberts算子的处理结果')
实现结果:

- 5. 引用文档
1-------------------------------------------------------------------百度百科
欢迎大家关注我的微信公众号FPGA开源工作室以及QQ群。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号