ATPG的D算法介绍

ATPG算法

实现测试向量自动化生成的算法，其中包含D算法、PODEM算法和FAN算法等。

D算法

为测试某一节点单固定故障，将其故障信息传递反映到输出中体现出来，我们把用穷举得出正确路径的方法称之为D算法。

每个节点分为四种状态，1、0、X、D和D(-)。

其中，X为0或1，意思是该节点值不影响最终结果。D为正常1故障0，D(-)为正常0故障1。

下面是一个D算法的实例

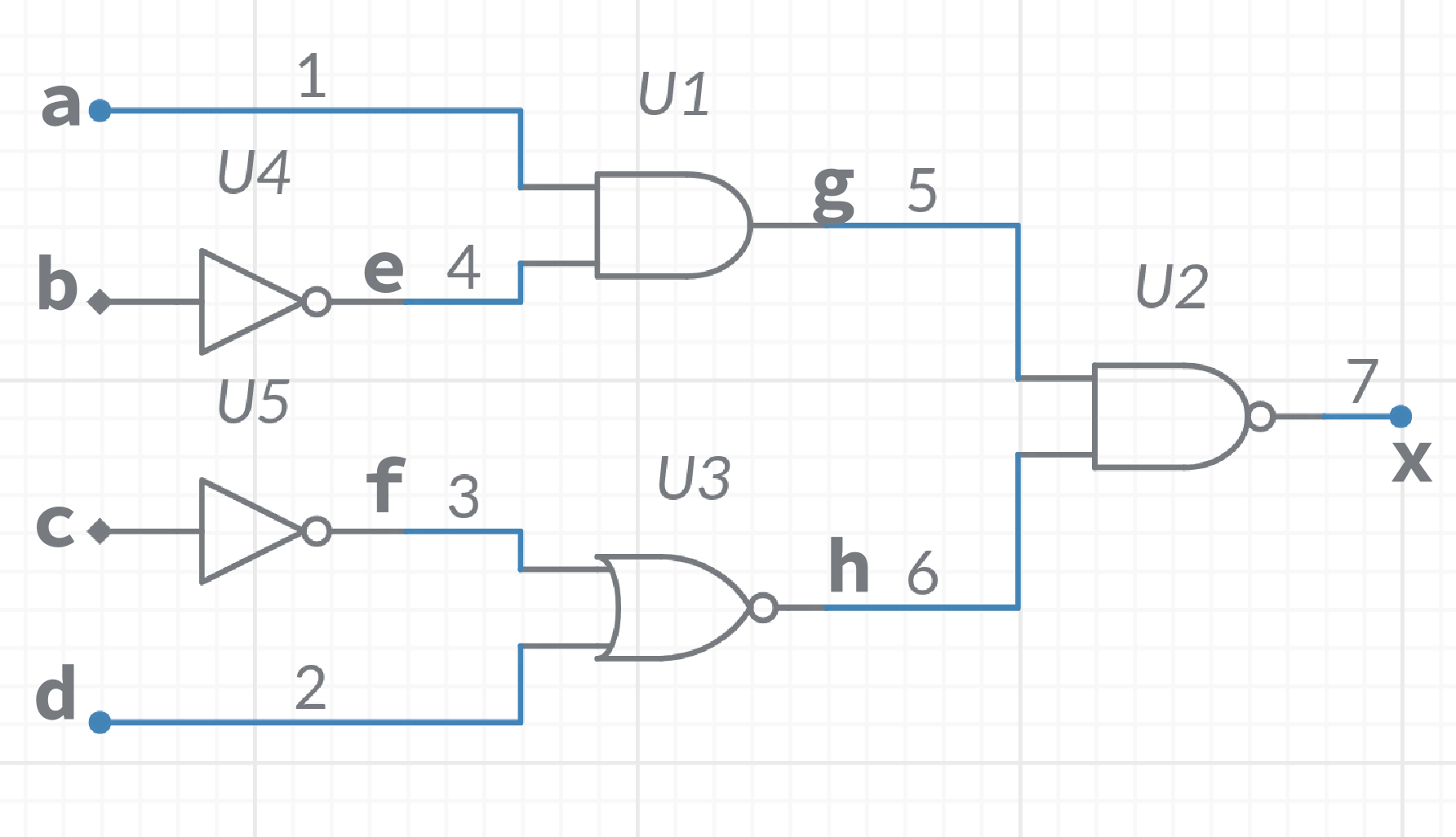
检测g单固定故障0

全步骤如下

步骤	a	b	c	d	e	f	g	h	x
激活	1				1		D
传播							D		D(-)
合理化							D	1	D(-)
回溯	1				1		D	1	D(-)
合理化				0		0		1
回溯	1			0	1	0	D	1	D(-)
合理化		0			1
回溯	1	0		0	1	0	D	1	D(-)
合理化			1			0
回溯	1	0	1	0	1	0	D	1	D(-)

最终我们可以得出测试向量为 1010，测试图形为 HLHL。

我们把激活故障的输入节点值集合称之为 奇异立方，传播时的路径称之为 敏化路径，d或d(-)出现在原始输出则为 追踪成功，回溯 的最终输入结果为测试图形。

其他算法

（待补充）

参考资料

• D算法介绍
• ATPG维基百科