理解方差、偏差且其泛化误差的关系
https://blog.csdn.net/ChenVast/article/details/81385018
| 符号 | 涵义 |
|---|---|
| 测试样本 | |
| 数据集 | |
| 训练集 |
|
| 由训练集 |
|
| 模型 |
方差
在一个训练集 D上模型 f对测试样本 x的预测输出为 f(x;D), 那么学习算法 f对测试样本 x的 期望预测 为:
上面的期望预测也就是针对 不同 数据集 D, f 对 x的预测值取其期望(平均预测)。
使用样本数相同的不同训练集产生的方差为:
偏差
期望预测与真实标记的误差称为偏差(bias), 为了方便起见, 我们直接取偏差的平方:
泛化误差
以回归任务为例, 学习算法的平方预测误差期望为:
对算法的期望泛化误差进行分解:
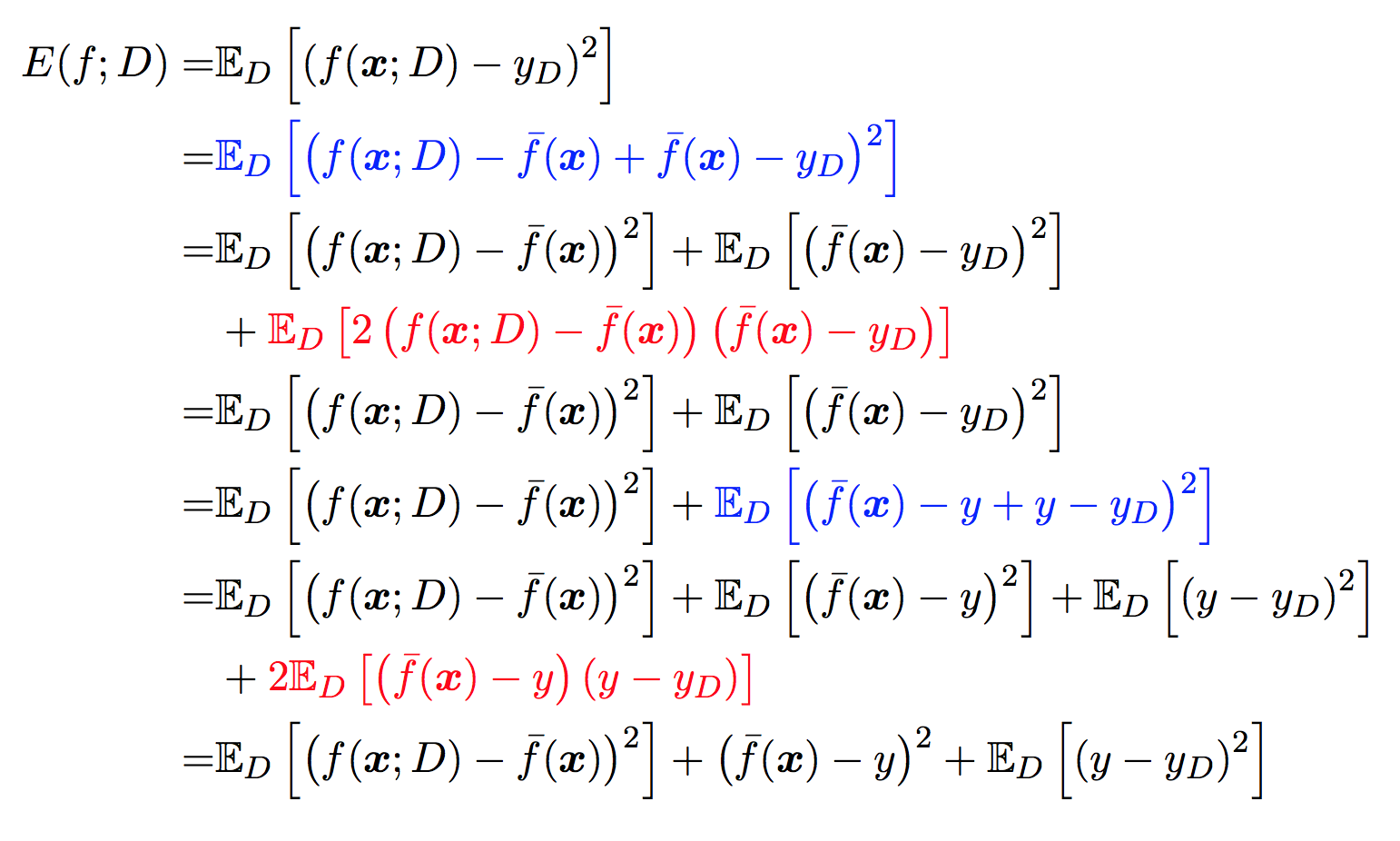
令噪声为零,,所以红色区域的等于零。
最后剩下 ,结果为泛化误差 = 偏差 + 方差 + 噪声
偏差、方差、噪声
- 偏差:度量了模型的期望预测和真实结果的偏离程度,刻画了模型本身的拟合能力。
- 方差:度量了同样大小的训练集的变动所导致的学习性能的变化,即刻画了数据扰动所造成的影响。
- 噪声:表达了当前任务上任何模型所能达到的期望泛化误差的下界,刻画了学习问题本身的难度。
图解偏差与方差
| 低方差 | 高方差 | |
| 低偏差 | 数据点集中+数据点落在预测点上 | 数据不集中+数据点部分落在预测点上(预测的准确率不高) |
| 高偏差 | 数据点集中+数据点与预测点存在距离(预测不准) | 数据点不集中+数据点基本不落在预测点上(预测不准) |
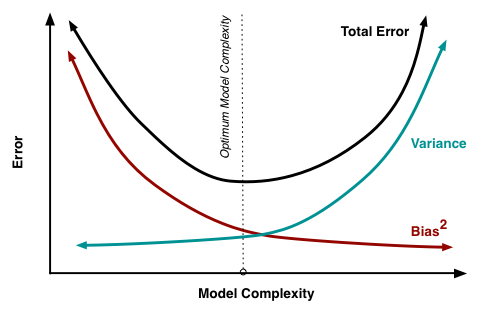
方差和偏差与拟合
| 拟合程度 | 方差 | 偏差 | 原因 | 解决办法 |
| 欠拟合 | 过高 | 训练不足,偏差主导泛化误差 | 集成学习;加深加迭代;加特征;降低正则化; | |
| 过拟合 | 过高 | 训练过多,方差主导泛化误差 | 降低模型复杂度;加正则惩罚项;加训练集;减特征;提高正则化 |
参考:
http://www.cnblogs.com/makefile/p/bias-var.html#fn2
版权声明:本文为博主原创文章,转载请在文章开头注明出处(作者+原文链接)。 https://blog.csdn.net/ChenVast/article/details/81385018










