如何理解深度学习中分布式训练中large batch size与learning rate的关系

转自：https://www.zhihu.com/people/xutan

最近在进行多GPU分布式训练时，也遇到了large batch与learning rate的理解调试问题，相比baseline的batch size，多机同步并行（之前有答案是介绍同步并行的通信框架NCCL（谭旭：如何理解Nvidia英伟达的Multi-GPU多卡通信框架NCCL？），有兴趣可以查看）等价于增大batch size，如果不进行精细的设计，large batch往往收敛效果会差于baseline的小batch size。因此将自己的理解以及实验总结如下，主要分为三个方面来介绍：（1）理解SGD、minibatch-SGD和GD，（2）large batch与learning rate的调试关系，（3）我们的实验。

（1）理解SGD、minibatch-SGD和GD

在机器学习优化算法中，GD（gradient descent）是最常用的方法之一，简单来说就是在整个训练集中计算当前的梯度，选定一个步长进行更新。GD的优点是，基于整个数据集得到的梯度，梯度估计相对较准，更新过程更准确。但也有几个缺点，一个是当训练集较大时，GD的梯度计算较为耗时，二是现代深度学习网络的loss function往往是非凸的，基于凸优化理论的优化算法只能收敛到local minima，因此使用GD训练深度神经网络，最终收收敛点很容易落在初始点附近的一个local minima，不太容易达到较好的收敛性能。

另一个极端是SGD（stochastic gradient descent）,每次计算梯度只用一个样本，这样做的好处是计算快，而且很适合online-learning数据流式到达的场景，但缺点是单个sample产生的梯度估计往往很不准，所以得采用很小的learning rate，而且由于现代的计算框架CPU/GPU的多线程工作，单个sample往往很难占满CPU/GPU的使用率，导致计算资源浪费。

折中的方案就是mini-batch，一次采用batch size的sample来估计梯度，这样梯度估计相对于SGD更准，同时batch size能占满CPU/GPU的计算资源，又不像GD那样计算整个训练集。同时也由于mini batch能有适当的梯度噪声[8]，一定程度上缓解GD直接掉进了初始点附近的local minima导致收敛不好的缺点，所以mini-batch的方法也最为常用。

关于增大batch size对于梯度估计准确度的影响，分析如下：

假设batch size为m，对于一个minibatch，loss为：

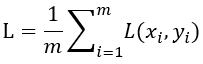
梯度

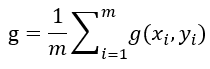
整个minibatch的梯度方差为：

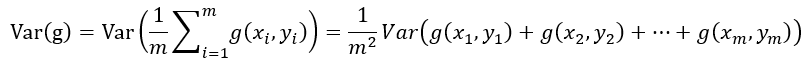
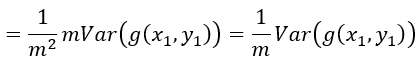
由于每个样本

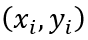
是随机从训练样本集sample得到的，满足i.i.d.假设，因此样本梯度的方差相等，为

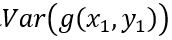
等价于SGD的梯度方差，可以看到batch size增大m倍，相当于将梯度的方差减少m倍，因此梯度更加准确。

如果要保持方差和原来SGD一样，相当于给定了这么大的方差带宽容量，那么就可以增大lr，充分利用这个方差容量，在上式中添加lr，同时利用方差的变化公式，得到等式

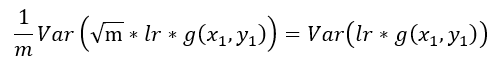
因此可将lr增加sqrt(m)倍，以提高训练速度，这也是在linear scaling rule之前很多人常用的增大lr的方式[4]。下一小节将详细介绍增大lr的问题。

（2）large batch与learning rate

在分布式训练中，batch size 随着数据并行的worker增加而增大，假设baseline的batch size为B，learning rate为lr，训练epoch数为N。如果保持baseline的learning rate，一般不会有较好的收敛速度和精度。原因如下：对于收敛速度，假设k个worker，每次过的sample数量为kB，因此一个epoch下的更新次数为baseline的1/k，而每次更新的lr不变，所以要达到baseline相同的更新次数，则需要增加epoch数量，最大需要增加k*N个epoch，因此收敛加速倍数会远远低于k。对于收敛精度，由于增大了batch size使梯度估计相较于badeline的梯度更加准确，噪音减少，更容易收敛到附近的local minima，类似于GD的效果。

为了解决这个问题，一个方法就是增大lr，因为batch变大梯度估计更准，理应比baseline的梯度更确信一些，所以增大lr，利用更准确的梯度多走一点，提高收敛速度。同时增大lr，让每次走的幅度尽量大一些，如果遇到了sharp local minima[8]（sharp minima的说法现在还有争议，暂且引用这个说法），还有可能逃出收敛到更好的地方。

但是lr不能无限制的增大，原因分析如下。深度神经网络的loss surface往往是高维高度非线性的，可以理解为loss surface表面凹凸不平，坑坑洼洼，不像y=x^2曲线这样光滑，因此基于当前weight计算出来的梯度，往前更新的learing rate很大的时候，沿着loss surface的切线就走了很大一布，有可能大大偏于原有的loss surface，示例如下图（a）所示，虚线是当前梯度的方向，也就是当前loss surface的切线方向，如果learning rate过大，那这一步沿切线方向就走了很大一步，如果一直持续这样，那很可能就走向了一个错误的loss surface，如图(b)所示。如果是较小的learning rate，每次只沿切线方向走一小步，虽然有些偏差，依然能大致沿着loss sourface steepest descent曲线想下降，最终收敛到一个不错的local minima，如图(c)所示。

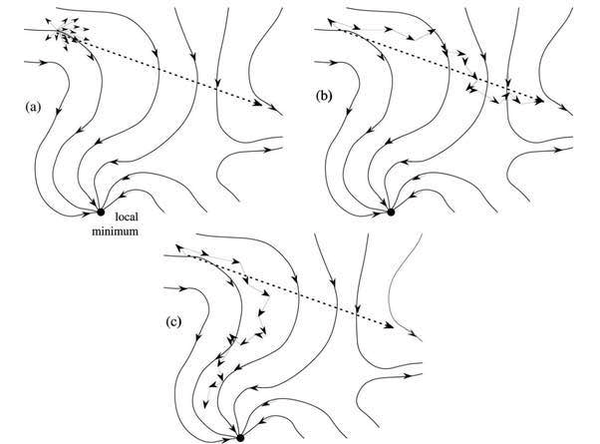
同时也可以根据convex convergence theory[2]得到lr的upper bound：lr<1/L，L为loss surface的gradient curve的Lipschitz factor，L可以理解为loss梯度的变化幅度的上界。如果变化幅度越大，L越大，则lr就会越小，如果变化幅度越小，L越小，则lr就可以很大。这和上图的分析是一致的。

因此，如何确定large batch与learing rate的关系呢？

分别比较baseline和k个worker的large batch的更新公式[7]，如下：

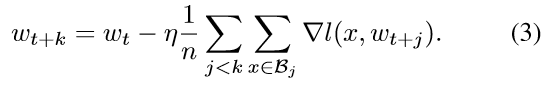
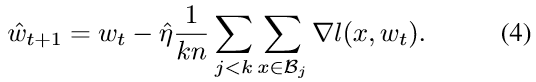
这个是baeline(batch size B)和large batch(batch size kB)的更新公式，（4）中large batch过一步的数据量相当于（3）中baseline k步过的数据量，loss和梯度都按找过的数据量取平均，因此，为了保证相同的数据量利用率，(4)中的learning rate应该为baseline的k倍，也就是learning rate的linear scale rule。

linear scale rule有几个约束，其中一个约束是关于weight的约束，式（3）中每一步更新基于的weight都是前一步更新过后的weight，因此相当于小碎步的走，每走一部都是基于目前真实的weight计算梯度做更新的，而式（4）的这一大步（相比baseline相当于k步）是基于t时刻的weight来做更新的。如果在这k步之内，W(t+j) ~ W(t)的话，两者近似没有太大问题，也就是linear scale rule问题不大，但在weight变化较快的时候，会有问题，尤其是模型在刚开始训练的时候，loss下特别快，weight变化很快，W(t+j) ~ W(t)就不满足。因此在初始训练阶段，一般不会直接将lr增大为k倍，而是从baseline的lr慢慢warmup到k倍，让linear scale rule不至于违背得那么明显，这也是facebook一小时训练imagenet的做法[7]。第二个约束是lr不能无限的放大，根据上面的分析，lr太大直接沿loss切线跑得太远，导致收敛出现问题。

同时，有文献[5]指出，当batchsize变大后，得到好的测试结果所能允许的lr范围在变小，也就是说，当batchsize很小时，比较容易找打一个合适的lr达到不错的结果，当batchsize变大后，可能需要精细地找一个合适的lr才能达到较好的结果，这也给实际的large batch分布式训练带来了困难。

（3）我们的实验

最近在考虑分布式训练NLP相关的深度模型的问题，实验细节如下，由于某些工作暂时还不方便透露，只提供较为简略的实验细节：

模型baseline参数为batch size 32， lr 0.25，最终的accuracy为BLEU score: 28.35。现在进行分布式扩展到多卡并行。

实验1：只增加并行worker数（也就相当于增大batch size），lr为baseline的lr0保持不变

可以看到随着batch的变大， 如果lr不变，模型的精度会逐渐下降，这也和上面的分析相符合。

实验2：增大batch size，lr相应增大

可以看到通过增加lr到5*lr0（理论上lr应该增加到8倍，但实际效果不好，因此只增加了5倍），并且通过warmup lr，达到和baseline差不多的Bleu效果。最终的收敛速度大约为5倍左右，也就是8卡能达到5倍的收敛加速（不考虑系统通信同步所消耗的时间，也就是不考虑系统加速比的情况下）。

深度学习并行训练能很好的提升模型训练速度，但是实际使用的过程中会面临一系列的问题，包括系统层面的架构设计、算法层面的参数调试等，欢迎有兴趣的朋友多多探讨。

[1] Li M, Zhang T, Chen Y, et al. Efficient mini-batch training for stochastic optimization[C]// Acm Sigkdd International Conference on Knowledge Discovery & Data Mining. ACM, 2014:661-670.

[2] Bottou L, Curtis F E, Nocedal J. Optimization Methods for Large-Scale Machine Learning[J]. 2016.

[3] Dekel O, Gilad-Bachrach R, Shamir O, et al. Optimal distributed online prediction using mini-batches[J]. Journal of Machine Learning Research, 2012, 13(1):165-202.

[4] Krizhevsky A. One weird trick for parallelizing convolutional neural networks[J]. Eprint Arxiv, 2014.

[5] Breuel T M. The Effects of Hyperparameters on SGD Training of Neural Networks[C]., 2015.

[6] Mishkin D, Sergievskiy N, Matas J. Systematic evaluation of CNN advances on the ImageNet[J]. 2016.

[7] Goyal, Priya, et al. "Accurate, Large Minibatch SGD: Training ImageNet in 1 Hour." arXiv preprint arXiv:1706.02677 (2017).

[8] Keskar N S, Mudigere D, Nocedal J, et al. On Large-Batch Training for Deep Learning: Generalization Gap and Sharp Minima[J]. 2016.

[9]Scaling Distributed Machine Learning with System and Algorithm Co-design - Google Search