二叉树的深度优先遍历（前序、中序、后序）

二叉树是一种非常重要的数据结构，很多其他数据机构都是基于二叉树的基础演变过来的。二叉树有前、中、后三种遍历方式，因为树的本身就是用递归定义的，因此采用递归的方法实现三种遍历，不仅代码简洁且容易理解，但其开销也比较大，而若采用非递归方法实现三种遍历，则要用栈来模拟实现（递归也是用栈实现的）。下面先简要介绍三种遍历方式的递归实现，再详细介绍三种遍历方式的非递归实现。

一、三种遍历方式的递归实现（比较简单，这里不详细讲解）

1、先序遍历——按照“根节点-左孩子-右孩子”的顺序进行访问。

void pre_traverse(BTree pTree)
{
    if(pTree)
    {
        printf(”%c ”,pTree->data);
        if(pTree->pLchild)
            pre_traverse(pTree->pLchild);
        if(pTree->pRchild)
            pre_traverse(pTree->pRchild);
    }
}

    2、中序遍历——按照“左孩子-根节点-右孩子”的顺序进行访问。

void in_traverse(BTree pTree)
{
    if(pTree)
    {
        if(pTree->pLchild)
            in_traverse(pTree->pLchild);
        printf(”%c ”,pTree->data);
        if(pTree->pRchild)
            in_traverse(pTree->pRchild);
    }
}

    3、后序遍历——按照“左孩子-右孩子-根节点”的顺序进行访问。

void beh_traverse(BTree pTree)
{
    if(pTree)
    {
        if(pTree->pLchild)
            beh_traverse(pTree->pLchild);
        if(pTree->pRchild)
            beh_traverse(pTree->pRchild);
        printf(”%c ”,pTree->data);
}

    二、三种遍历方式的非递归实现

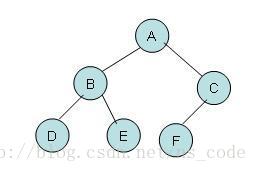
    为了便于理解，这里以下图的二叉树为例，分析二叉树的三种遍历方式的实现过程。

          1、前序遍历的非递归实现 

根据先序遍历的顺序，先访问根节点，再访问左子树，后访问右子树，而对于每个子树来说，又按照同样的访问顺序进行遍历，上图的先序遍历顺序为：ABDECF。非递归的实现思路如下：

对于任一节点P，

1）输出节点P，然后将其入栈，再看P的左孩子是否为空；

2）若P的左孩子不为空，则置P的左孩子为当前节点，重复1）的操作；

3）若P的左孩子为空，则将栈顶节点出栈，但不输出，并将出栈节点的右孩子置为当前节点，看其是否为空；

4）若不为空，则循环至1）操作；

5）如果为空，则继续出栈，但不输出，同时将出栈节点的右孩子置为当前节点，看其是否为空，重复4）和5）操作；

6）直到当前节点P为NULL并且栈空，遍历结束。

   

   下面以上图为例详细分析其先序遍历的非递归实现过程：

首先，从根节点A开始，根据操作1），输出A，并将其入栈，由于A的左孩子不为空，根据操作2），将B置为当前节点，再根据操作1），将B输出，并将其入栈，由于B的左孩子也不为空，根据操作2），将D置为当前节点，再根据操作1），输出D，并将其入栈，此时输出序列为ABD；

由于D的左孩子为空，根据操作3），将栈顶节点D出栈，但不输出，并将其右孩子置为当前节点；

由于D的右孩子为空，根据操作5），继续将栈顶节点B出栈，但不输出，并将其右孩子置为当前节点；

由于B的右孩子E不为空，根据操作1），输出E，并将其入栈，此时输出序列为：ABDE；

由于E的左孩子为空，根据操作3），将栈顶节点E出栈，但不输出，并将其右孩子置为当前节点；

由于E的右孩子为空，根据操作5），继续将栈顶节点A出栈，但不输出，并将其右孩子置为当前节点；

由于A的右孩子C不为空，根据操作1），输出C，并将其入栈，此时输出序列为：ABDEC；

由于A的左孩子F不为空，根据操作2），则将F置为当前节点，再根据操作1），输出F，并将其入栈，此时输出序列为：ABDECF；

由于F的左孩子为空，根据操作3），将栈顶节点F出栈，但不输出，并将其右孩子置为当前节点；

由于F的右孩子为空，根据操作5），继续将栈顶元素C出栈，但不输出，并将其右孩子置为当前节点；

此时栈空，且C的右孩子为NULL，因此遍历结束。

   根据以上思路，前序遍历的非递归实现代码如下：

void pre_traverse(BTree pTree)
{
    PSTACK stack = create_stack();  //创建一个空栈
    BTree node_pop;                 //用来保存出栈节点
    BTree pCur = pTree;             //定义用来指向当前访问的节点的指针

    //直到当前节点pCur为NULL且栈空时，循环结束
    while(pCur || !is_empty(stack))
    {
        //从根节点开始，输出当前节点，并将其入栈，
        //同时置其左孩子为当前节点，直至其没有左孩子，及当前节点为NULL
        printf(”%c ”, pCur->data);
        push_stack(stack,pCur);
        pCur = pCur->pLchild;
        //如果当前节点pCur为NULL且栈不空，则将栈顶节点出栈，
        //同时置其右孩子为当前节点,循环判断，直至pCur不为空
        while(!pCur && !is_empty(stack))
        {
            pCur = getTop(stack);
            pop_stack(stack,&node_pop);
            pCur = pCur->pRchild;
        }
    }
}

   2、中序遍历的非递归实现

根据中序遍历的顺序，先访问左子树，再访问根节点，后访问右子树，而对于每个子树来说，又按照同样的访问顺序进行遍历，上图的中序遍历顺序为：DBEAFC。非递归的实现思路如下：

对于任一节点P，

1）若P的左孩子不为空，则将P入栈并将P的左孩子置为当前节点，然后再对当前节点进行相同的处理；

2）若P的左孩子为空，则输出P节点，而后将P的右孩子置为当前节点，看其是否为空；

3）若不为空，则重复1）和2）的操作；

4）若为空，则执行出栈操作，输出栈顶节点，并将出栈的节点的右孩子置为当前节点，看起是否为空，重复3）和4）的操作；

5）直到当前节点P为NULL并且栈为空，则遍历结束。

   下面以上图为例详细分析其中序遍历的非递归实现过程：

首先，从根节点A开始，A的左孩子不为空，根据操作1）将A入栈，接着将B置为当前节点，B的左孩子也不为空，根据操作1），将B也入栈，接着将D置为当前节点，由于D的左子树为空，根据操作2），输出D；

由于D的右孩子也为空，根据操作4），执行出栈操作，将栈顶结点B出栈，并将B置为当前节点，此时输出序列为DB；

由于B的右孩子不为空，根据操作3），将其右孩子E置为当前节点，由于E的左孩子为空，根据操作1），输出E，此时输出序列为DBE；

由于E的右孩子为空，根据操作4），执行出栈操作，将栈顶节点A出栈，并将节点A置为当前节点，此时输出序列为DBEA；

此时栈为空，但当前节点A的右孩子并不为NULL，继续执行，由于A的右孩子不为空，根据操作3），将其右孩子C置为当前节点，由于C的左孩子不为空，根据操作1），将C入栈，将其左孩子F置为当前节点，由于F的左孩子为空，根据操作2），输出F，此时输出序列为：DBEAF；

由于F的右孩子也为空，根据操作4），执行出栈操作，将栈顶元素C出栈，并将其置为当前节点，此时的输出序列为：DBEAFC；

由于C的右孩子为NULL，且此时栈空，根据操作5），遍历结束。

    根据以上思路，中序遍历的非递归实现代码如下：

void in_traverse(BTree pTree)
{
    PSTACK stack = create_stack();  //创建一个空栈
    BTree node_pop;                 //用来保存出栈节点
    BTree pCur = pTree;             //定义指向当前访问的节点的指针

    //直到当前节点pCur为NULL且栈空时，循环结束
    while(pCur || !is_empty(stack))
    {
        if(pCur->pLchild)
        {
            //如果pCur的左孩子不为空，则将其入栈，并置其左孩子为当前节点
            push_stack(stack,pCur);
            pCur = pCur->pLchild;
        }
        else
        {
            //如果pCur的左孩子为空，则输出pCur节点，并将其右孩子设为当前节点，看其是否为空
            printf(”%c ”, pCur->data);
            pCur = pCur->pRchild;
            //如果为空，且栈不空，则将栈顶节点出栈，并输出该节点，
            //同时将它的右孩子设为当前节点，继续判断，直到当前节点不为空
            while(!pCur && !is_empty(stack))
            {
                pCur = getTop(stack);
                printf(”%c ”,pCur->data);
                pop_stack(stack,&node_pop);
                pCur = pCur->pRchild;
            }
        }
    }
}

   3、后序遍历的非递归实现

根据后序遍历的顺序，先访问左子树，再访问右子树，后访问根节点，而对于每个子树来说，又按照同样的访问顺序进行遍历，上图的后序遍历顺序为：DEBFCA。后序遍历的非递归的实现相对来说要难一些，要保证根节点在左子树和右子树被访问后才能访问，思路如下：

对于任一节点P，

1）先将节点P入栈；

2）若P不存在左孩子和右孩子，或者P存在左孩子或右孩子，但左右孩子已经被输出，则可以直接输出节点P，并将其出栈，将出栈节点P标记为上一个输出的节点，再将此时的栈顶结点设为当前节点；

3）若不满足2）中的条件，则将P的右孩子和左孩子依次入栈，当前节点重新置为栈顶结点，之后重复操作2）；

4）直到栈空，遍历结束。

   下面以上图为例详细分析其后序遍历的非递归实现过程：

首先，设置两个指针：Cur指针指向当前访问的节点，它一直指向栈顶节点，每次出栈一个节点后，将其重新置为栈顶结点，Pre节点指向上一个访问的节点；

Cur首先指向根节点A，Pre先设为NULL，由于A存在左孩子和右孩子，根据操作3），先将右孩子C入栈，再将左孩子B入栈，Cur改为指向栈顶结点B；

由于B的也有左孩子和右孩子，根据操作3），将E、D依次入栈，Cur改为指向栈顶结点D；

由于D没有左孩子，也没有右孩子，根据操作2），直接输出D，并将其出栈，将Pre指向D，Cur指向栈顶结点E，此时输出序列为：D；

由于E也没有左右孩子，根据操作2），输出E，并将其出栈，将Pre指向E，Cur指向栈顶结点B，此时输出序列为：DE；

由于B的左右孩子已经被输出，即满足条件Pre==Cur->lchild或Pre==Cur->rchild，根据操作2），输出B，并将其出栈，将Pre指向B，Cur指向栈顶结点C，此时输出序列为：DEB；

由于C有左孩子，根据操作3），将其入栈，Cur指向栈顶节点F；

由于F没有左右孩子，根据操作2），输出F，并将其出栈，将Pre指向F，Cur指向栈顶结点C，此时输出序列为：DEBF；

由于C的左孩子已经被输出，即满足Pre==Cur->lchild，根据操作2），输出C，并将其出栈，将Pre指向C，Cur指向栈顶结点A，此时输出序列为：DEBFC；

由于A的左右孩子已经被输出，根据操作2），输出A，并将其出栈，此时输出序列为：DEBFCA；

此时栈空，遍历结束。

   根据以上思路，后序遍历的非递归实现代码如下：

void beh_traverse(BTree pTree)
{
    PSTACK stack = create_stack();  //创建一个空栈
    BTree node_pop;          //用来保存出栈的节点
    BTree pCur;              //定义指针，指向当前节点
    BTree pPre = NULL;       //定义指针，指向上一各访问的节点

    //先将树的根节点入栈
    push_stack(stack,pTree);
    //直到栈空时，结束循环
    while(!is_empty(stack))
    {
        pCur = getTop(stack);   //当前节点置为栈顶节点
        if((pCur->pLchild==NULL && pCur->pRchild==NULL) ||
            (pPre!=NULL && (pCur->pLchild==pPre || pCur->pRchild==pPre)))
        {
            //如果当前节点没有左右孩子，或者有左孩子或有孩子，但已经被访问输出，
            //则直接输出该节点，将其出栈，将其设为上一个访问的节点
            printf(”%c ”, pCur->data);
            pop_stack(stack,&node_pop);
            pPre = pCur;
        }
        else
        {
            //如果不满足上面两种情况,则将其右孩子左孩子依次入栈
            if(pCur->pRchild != NULL)
                push_stack(stack,pCur->pRchild);
            if(pCur->pLchild != NULL)
                push_stack(stack,pCur->pLchild);
        }
    }
}

    以上遍历算法在VC上实现的输出结果如下：

   完整代码下载地址（自己的劳动成果，需要2个积分，大家多多谅解）：http://download.csdn.net/detail/mmc_maodun/6445579