机器学习lab4

​

一.实验目标

实现一个PCA模型，能够对给定数据进行降维（即找到其中的主成分）

二.实验要求和实验环境

实验要求

测试：

（1）首先人工生成一些数据（如三维数据），让它们主要分布在低维空间中，如首先让某个维度的方差远小于其它唯独，然后对这些数据旋转。生成这些数据后，用你的PCA方法进行主成分提取。

（2）找一个人脸数据（小点样本量），用你实现PCA方法对该数据降维，找出一些主成分，然后用这些主成分对每一副人脸图像进行重建，比较一些它们与原图像有多大差别（用信噪比衡量）。

实验环境

• Microsoft win10 1809

• python 3.7.0

• Sublime Text 3

三.设计思想

1.算法原理

1.1 坐标变换

1. 对于数据集​，其中​。先对每个样本进行中心化, 即：

其中​称为样本集的​的中心向量。之所以进行中心化，是因为经过中心化之后的常规的线性变换就是绕原点的旋转变化，也就是坐标变换；

2. 以及​就是样本集的协方差矩阵。经过中心化后的数据，有​。设使用的投影坐标系的标准正交向量基:​，每个样本降维后得到的坐标为:

3. 因此，样本集与降维后的样本集表示为：

因此降维的物理意义为：通过线性组合原始特征，从而去掉一些冗余的或者不重要的特征、保留重要的特征。

1.2 重构后的误差

在得到​后，需要对其进行重构，重构后的样本设为

将式​代入，那么对于整个数据集上的所有样本与重构后的样本之间的误差为:

根据定义，可以有：

由于​是标量，有​，从而式​变为：

此外，根据​的定义有：

结合式​可以化简优化目标：

从而优化目标为​，约束为​

对于原始数据样本点​在降维后在新空间的超平面上的投影为​。若使样本点的投影尽可能分开，应该使样本点在投影后的方差最大化，即使下式最大化：

可以看到式​与​等价。PCA的优化问题就是要求解​的特征值。

只需将​进行特征值分解，将得到的特征值进行排序：​，提取前​大的特征值对应的单位特征向量即可构成变化矩阵​。

2.算法的实现

给定样本集​和低维空间的维数​

1. 对所有的样本进行中心化操作：

   1. 计算样本均值​

   2. 所有样本减去均值​

2. 计算样本的协方差矩阵​

3. 对协方差矩阵​进行特征值分解

4. 取最大的​个特征值对应的单位特征向量​，构造投影矩阵​

5. 输出投影矩阵​与样本均值​

四、实验结果与分析

3D数据测试

产生数据: 3维高斯分布随机产生100个样本，参数为：

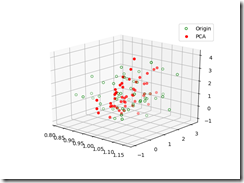
降维后,还原的点如下图所示:

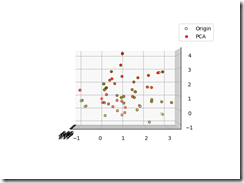
其中绿色的点是源数据点, 红色的点是降维后有还原到原空间的点.

从上图可以看到数据都在一个平面上, 说明我们的却对数据降了一个维度.

可以看到降维后的数据与元数据在二维视图中基本重合, 说明我们的降维是成功的.

人脸数据

数据源: BioID人脸数据库

说明

该数据集由1521张灰度图像组成，分辨率为384x286像素。每个人都展示了23个不同测试人员中一个人的面部正视图。出于比较原因，该组还包含手动设置的眼位。这些图像被标记为“ BioID_xxxx.pgm”，其中字符xxxx被当前图像的索引替换（前导零）。与此类似，文件“ BioID_xxxx.eye”包含相应图像的眼睛位置。

图像文件格式

使用便携式灰度图（pgm）数据格式将图像存储在单个文件中。pgm文件包含一个数据头，后跟图像数据。在我们的例子中，标题由四行文本组成。

• 第一行描述了图像数据的格式（ASCII /二进制）。在我们的文件中，文本“ P5”表示数据以二进制形式写入

• 第二行包含以文本形式编写的图像宽度

• 第三行还将图像高度保持为文本形式

• 第四行包含允许的最大灰度值（在我们的图像中为255）

标题后跟一个包含图像数据的数据块。数据从上到下每行使用每个像素一个字节存储。

降维对比:

说明:1,3列为原图, 2,4列为降维后还原的图片:

可以看出, 当维度降为150度时, 还原后的图片基本上只能看到大概轮廓.

相比于150维, 300略为清晰.

500维时,较清晰.

1000维时, 基本和原图差异不大.

计算信噪比

计算公式如下:

取不同维度测试信噪比,令降维后的维度为以下:

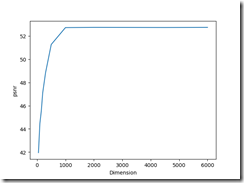
计算每个维度取值得出的信噪比, 画出信噪比变化曲线,如下:

可以看到, 维度在0 - 1000之间时, psnr随着维度的增加迅速增加, 这是因为随着维度的增加, 降维后的数据越来越接近源数据.

当维度超过1500时, psnr的基本不发生变化, 这是因为1500维已经刻画了绝大多数的信息, 再多的维度已经不能提供更多更明显的信息了.

五、结论

• 数据降维后会保留主要特征, 即主要成分, 不重要的特征将被忽略

• 数据降维后的却会丢失一部分信息, 降维降得越多, 丢失的信息越多

• 从psnr的曲线中可以看出, 15000维左右的数据就几乎可以刻画原图

六、参考文献

1. Pattern Recognition and Machine Learning.

2. 统计学习方法

3. 人脸数据

七、附录：源代码（带注释）

 # author: lgq
 # time 2019/11/3
 # 机器学习, 降维, lab4
 import numpy as np
 import os
 from matplotlib import pyplot as plt
 from mpl_toolkits.mplot3d import Axes3D
 from os import walk, path
 import mahotas as mh
 ​
 ​
 hight ,width = 286,  384  # 图片尺寸
 k = 4   # 压缩比
 m,n = hight//k, width//k   # 压缩之后的图片
 ​
 ​
 def generate_data(data_size):
     mean = [1, 1, 1]
     cov = [[0.01, 0, 0], [0, 1, 0], [0, 0, 1]]
     data = np.random.multivariate_normal(mean, cov,data_size)
     return data
 ​
 ​
 def draw_data(origin_data, pca_data_inverse):
     fig = plt.figure()
     ax = fig.gca(projection='3d')
     ax.scatter(origin_data[:, 0], origin_data[:, 1], origin_data[:, 2],
                facecolor="none", edgecolor="g", label='Origin')
     ax.scatter(pca_data_inverse[:, 0], pca_data_inverse[:, 1], pca_data_inverse[:, 2], facecolor='r', label='PCA')
     plt.legend()
     plt.show()
 ​
 ​
 def pca(data, reduced_dimension):
     rows, columns = data.shape
     assert reduced_dimension <= columns
     x_mean = 1.0 / rows * np.sum(data,  axis=0)
     decentralise_x = data - x_mean  # 去中心化
     cov = decentralise_x.T.dot(decentralise_x)  # 计算协方差
     eigenvalues, feature_vectors = np.linalg.eig(cov)  # 特征值分解
     min_d = np.argsort(eigenvalues)
     feature_vectors = np.delete(feature_vectors, min_d[:columns - reduced_dimension], axis=1)
     return feature_vectors, x_mean  
 ​
 def psnr(source, target):
     """ 计算信噪比 """
     diff = source - target
     diff = diff ** 2
     rmse = np.sqrt(np.mean(diff))
     return 20 * np.log10(255.0 / rmse)
 ​
 ​
 ​
 ​
 def test_3D_data():
     data_size = 100
     data = generate_data(data_size)
     w, mu_data = pca(data,2)
     pca_data = (data - mu_data).dot(w)
     pca_data_inverse = pca_data.dot(w.T) + mu_data
     draw_data(data, pca_data_inverse)
 ​
 ​
 # 载入脸部数据
 def load_face_data(filepath):
     x = []
     for dir_path, dir_names, file_names in walk(filepath):
        #walk() 函数内存放的是数据的绝对路径，同时注意斜杠的方向。
        for fn in file_names:
             if fn[-3:] == 'pgm':
                 image_filename = path.join(dir_path, fn)
                 x.append(mh.imread(image_filename, as_grey=True).reshape(109824))
     return np.array(x)
 ​
 ​
 # 将face矩阵数据压缩并存储在txt中
 def compress_data(x_train,only_part = False):
     data_size = len(x_train)
     k = 4
     c = np.zeros((data_size,m,n))
     for pgm in range(data_size):
         if not pgm %100:
             print('compress:',100*pgm/data_size,'%') # 输出压缩进度
         img =x_train[pgm].reshape(hight, width)
         for i in range(m):
             for j in range(n):
                 c[pgm,i,j] = (np.sum(img[k*i:k*i+1,k*j:k*j+1]))/(k*k)
     if only_part:
         np.savetxt(str(k)+'_compress_face_data_part.txt',c[0:200].reshape(200,m*n).astype('int32'))
     else:
         np.savetxt(str(k)+'_compress_face_data.txt',c.reshape(data_size,m*n).astype('int32'))
 ​
 ​
 ​
 ​
 def draw_face_data(data,pca_data_inverse,d):
     fig, ax = plt.subplots(nrows=5, ncols=4, sharex='all', sharey='all')
     ax = ax.flatten()
     for i in range(10):
         if i >100:
             break
         img = data[i*10].reshape(m, n)
         ax[2 * i].imshow(img, cmap='Greys')
         img_compared = pca_data_inverse[i*10].reshape(m, n)
         ax[2 * i + 1].imshow(img_compared, cmap='Greys', interpolation='nearest')
     ax[0].set_xticks([])
     ax[0].set_yticks([])
     plt.tight_layout()
     plt.title('Dimension = ' + str(d))
     plt.show()
 ​
 def test_face_data():
     # data = np.loadtxt('4_compress_face_data.txt')
     data = np.loadtxt('4_compress_face_data_part.txt')
     data = data.reshape((len(data),m*n))
 ​
     print('load finish; data.shape:',data.shape,type(data[1,1]))
     data = data.astype('float32') # 求过程中会变为小数  
 ​
     d = 300 # 压缩后的维度
     w, mu = pca(data, d)
     print('pca finish')
 ​
     pca_data_inverse = (data - mu).dot(w).dot(w.T) + mu
     pca_data_inverse = pca_data_inverse.astype(np.int)
    
     draw_face_data(data,pca_data_inverse,d)
 ​
 def test_psnr():
     d_list = [50,100,150,200,300,500,1000,2000,3000,4500,6000]
     psnr_list = []
     data = np.loadtxt('4_compress_face_data.txt')
     data = data.astype('float32')
     print('load finish; data.shape:',data.shape,type(data[1,1]))
 ​
     rows, columns = data.shape
     x_mean = 1.0 / rows * np.sum(data,  axis=0)
     decentralise_x = data - x_mean  # 去中心化
     cov = decentralise_x.T.dot(decentralise_x)  # 计算协方差
     eigenvalues, feature_vectors = np.linalg.eig(cov)  # 特征值分解
     # np.savetxt('eigenvalues.txt',eigenvalues)
     # np.savetxt('feature_vectors.txt',feature_vectors)
     min_d = np.argsort(eigenvalues)
     print('...')
     for d in d_list:
         assert d <= columns
         feature_vectors_chooose = np.delete(feature_vectors, min_d[:columns - d], axis=1) 
         w, mu = feature_vectors_chooose, x_mean 
         pca_data_inverse = (data - mu).dot(w).dot(w.T) + mu
         pca_data_inverse = pca_data_inverse.astype(np.int)
         
         psnr_list.append(psnr(data[10],pca_data_inverse[10]))
         print('...')
     plt.plot(d_list,psnr_list)
     plt.xlabel('Dimension')
     plt.ylabel('psnr')
     plt.show()
 ​
 def main():
     # 测试随机生成的三维数据
     test_3D_data()
 ​
     # 测试脸部数据
     # test_face_data()
 ​
     # 测试信噪比
     # test_psnr()
     
 ​
 ​
 ​
 if __name__ == '__main__':
     main()