基于深度学习的自然图像和医学图像分割:损失函数设计(2)
创建日期: 2020-02-17 16:45:35
上一篇文章总结了在图像分割问题中,常用的经典损失函数,包括基于交叉熵和基于重叠度两大系列损失函数。这篇介绍一下损失函数在医学图像分割问题中的应用。
1. 损失函数在医学图像分割中的应用
上一篇文章中我们讨论了标准的交叉熵损失函数及其加权版本,这些损失函数也都广泛应用在医学图像分割问题中。但是针对大背景中的小前景对象分割问题(常见于医学图像,典型的类别不平衡),基于重叠度的损失函数(例如Dice Loss),优化效果要好于原始的交叉熵损失函数。医学图像种类丰富,具体的分割问题可以加入先验知识来提高优化效果,下面介绍一些在医学图像分割问题中比较经典的损失函数。
\1. Li提出了一种对交叉熵损失函数进行改进的正则化项:
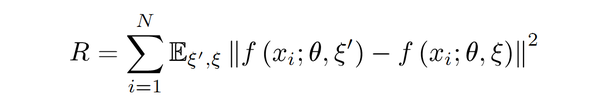
其中, \xi ^{'} 和
\xi 是针对输入图像
x_i 的不同扰动或噪声(例如高斯噪声,网络Dropout策略,随机数据增广) 。
\2. Xu提出了将传统的主动轮廓能量最小化应用到卷积神经网络优化的损失函数:
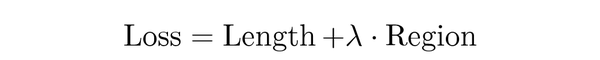
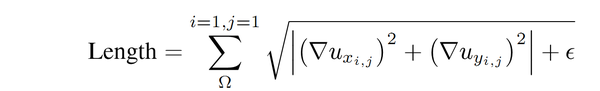
第一项中的 u_{x_{i,j}} 和
u_{y_{i,j}}中的
x 和
y 分别表示水平和垂直方向。
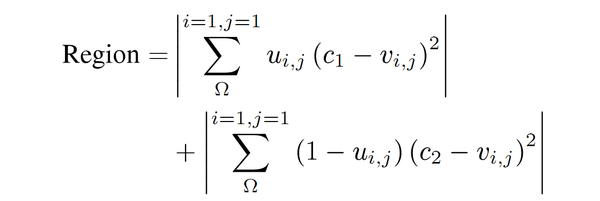
第二项中 u 和
v 分别表示预测结果和给定图像(GT),C1设置为1,c2设置为0,并且将轮廓回归项添加到加权交叉熵损失函数中。
\3. Karimi提出了一种基于Hausdorff距离(HD)的损失函数:
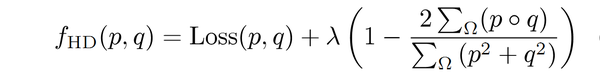
其中第二项是Dice Loss。
第一项可以用三种不同版本的Hausdorff Distance替换, 式中的 p 和
q 分别表示Ground Truth和分割预测结果。三个可替换版本分别为:
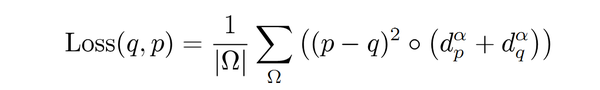
Loss(p,q)版本一
其中,参数 \alpha 决定较大误差的惩罚级别。
d_p 是Ground-truth分割的距离图,即到边界
\delta_p 的无符号距离。 同样
d_q 被定义为到
\delta_q 的距离。
\circ 表示的是hadamard操作,即同阶矩阵对应元素相乘作为矩阵元素,也可以认为是矩阵点乘。
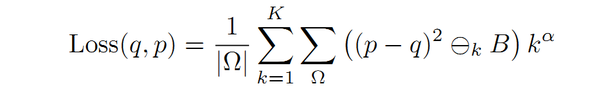
Loss(p,q)版本二
其中, \ominus_k 表示k次连续腐蚀操作,腐蚀结构元为:
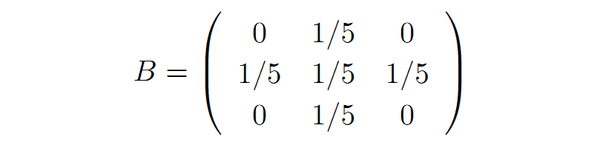
腐蚀结构元
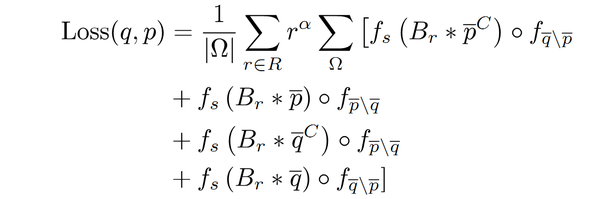
Loss(p,q)版本三
其中, f_{\bar{q} \setminus \bar{p}}=(p-q)^2q ,
f_s 表示软化阈值。Br表示半径为r的圆形卷积核。 Br的元素经过归一化以使其元素和为1。
\bar{p}^C=1-\bar{p} 。式中的
\bar{p} 和
\bar{q} 分别表示Ground Truth和分割预测结果。
\4. Caliva等人提出通过测量每个体素到对象边界的距离,并使用权重矩阵对边界误差进行惩罚。 Kim等人提出使用水平集能量最小化( level-set energy minimization)作为正则化器,再加上标准的多类交叉熵损失函数,来用于半监督的脑MRI图像分割,损失函数如下所示:
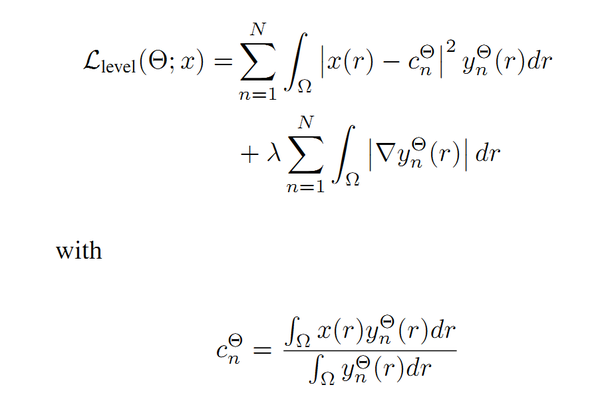
其中, x(r) 是输入,
y_{n}^{\ominus} 是softmax层的输出,
\ominus 表示可学习参数。
\5. Taghanaki等人发现使用单独的基于重叠度的损失函数存在风险,并提出将基于重叠度的损失函数(Dice Loss)作为正则化项与加权交叉熵(WCE)结合构成新的损失函数——Combo Loss,以处理输入和输出不平衡问题,公式如下所示:
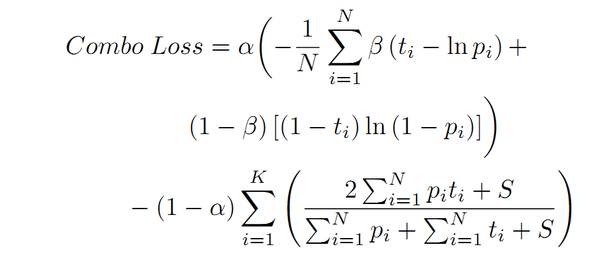
其中, \alpha 因子用来控制Dice Loss(第二部分)对Loss函数的贡献,
\alpha 越大对Loss的贡献越大。
\beta\in[0,1] 用来控制模型对FN/FP的惩罚程度:当
\beta 设置为小于0.5的值时,由于给予
(1-t_i)ln(1-p_i) 权重更大,因此对FP的惩罚要大于FN,反之亦然。 在具体的实现中,为防止除零问题出现,我们使用了加一平滑(加性/拉普拉斯/里德斯通平滑等),即向Dice Loss项的分母和分子都加上单位常数S 。
小结:本文讨论的大多数方法都尝试通过在损失函数中加入权重/惩罚项来处理输入图像中的类不平衡问题,即小前景与大背景的问题。 还有一些先检测后分割(级联分割)的方法,首先检测感兴趣对象,然后在检测框(矩形框)内完成分割任务(类似于mask-rcnn), 这种级联的方法已应用于脊髓多发性硬化病灶的分割。
2. 总结
上面提到的损失函数是一些设计的比较出色的损失函数。不同于自然图像,类不平衡问题在医学图像中很常见,在上一篇损失函数设计:李慕清:基于深度学习的自然图像和医学图像分割:损失函数设计(1)中,在文末我们对比了不同损失函数的优化效果,这里我们再来总结一下,如下图所示:
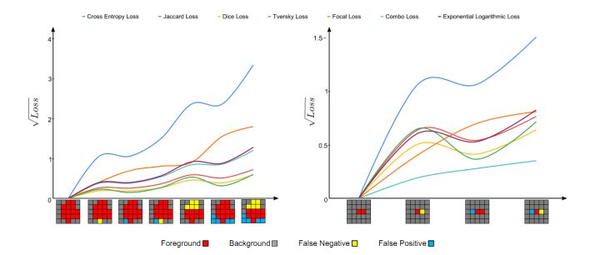
上图将不同损失函数的表现进行了可视化(分别为分割大型(左)和小型对象(右))。 其中每张小图底部的可视化分割结果,从左向右,预测结果和GroundTruth的重叠逐渐变小,即产生更多的假阳性(FP)和假阴性(FN)。 理想情况下,Loss函数的值应随着预测更多的假阳性和假阴性而单调增加。 对于大型对象(左图),几乎所有现象都遵循此假设; 但是,对于小型对象(右图),只有combo loss和focal loss会因较大的误差而单调增大更多。 换句话说,在分割大/小对象时,基于重合度(重叠度)的损失函数波动很大,这导致优化过程的不稳定。 使用交叉熵作为基础的损失函数和重叠度作为加权正则函数的损失(combo loss)函数在训练过程中显示出更高的稳定性。
损失函数作为深度学习模型里的独立模块,可以自由替换,所以可以在训练的不同阶段选择不同的损失函数。设计医学图像分割的损失函数加入先验信息是有效的,但同时也限制了其对其他类型数据的泛化能力,有得有失,只能权衡一下了。
后续再对这些常用的这些损失函数进行Python(pytorch框架)实现。
参考文献:



 浙公网安备 33010602011771号
浙公网安备 33010602011771号