基于深度学习的自然图像和医学图像分割：损失函数设计(1)

创建日期: 2020-02-17 16:45:29

本文总结一下基于深度学习的自然图像和医学图像分割问题中，常用的损失函数。

从频率派的角度看深度学习模型，是把输入数据 X 假设为一个随机变量，服从一个概率分布 X\sim P(x|\theta) , 其中的参数 \theta 是未知常量。我们需要对 \theta 进行求解，但深度学习模型直接得到解析解是不可能的，我们只能求得 \tilde{\theta} 来逼近 \theta 。损失函数就是作为优化过程的指导，衡量模型预测结果与真实标签之间的“差距”，然后通过梯度反向传播来不断修正 \tilde{\theta} 使其趋近于 \theta ，这个过程就是优化。这样模型参数的求解问题转化为一个最优化问题。图像语义分割问题可视为一个像素级分类问题，因此最常用的分类损失函数——交叉熵损失函数，可以用于图像语义分割，发展出基于交叉熵的损失函数系列；图像分割结果是一个mask（或概率图），计算预测mask（或概率图）与ground truth的重合度可以直接度量模型的分割性能，基于此发展出基于重合度度量（如IoU）的损失函数系列。下面分别进行详细介绍：

1.基于交叉熵的损失函数系列

这个系列损失函数基于交叉熵理论进行设计，通过逐像素计算预测分布与groundtruth分布之间的“差距”得到损失函数的值。数学上可证明交叉熵损失函数等价于最大似然估计。

1.1 交叉熵（Cross Entorpy,CE）

交叉熵损失函数逐像素对比了模型预测向量与one-hot编码后的groundtruth，在二类分割问题中，令：

P(Y=1)=p

%3D1-p\)P(Y=0)=1-p\

其中， Y=1,0 分别表示标签为阳性和阴性。在分割问题中，groundtruth是已知的，即 p=0,1。

模型的概率预测结果可以由sigmoid函数（或softmax）计算得到，令：

%3D\frac{1}{1%2Be^x}%3D\hat{p}\)P(\hat{Y}=1)=\frac{1}{1+e}x}=\hat{p}\

P(\hat{Y}=0)=1-\frac{1}{1+e^x}=1-\hat{p}

其中，x 是模型的输出，后接sigmoid函数可以将其转为概率结果（即各类预测概率之和为1）， \hat{Y}=1,0 分别表示预测为阳性和阴性。

那么二分类交叉熵损失函数可以定义为：

CE(p,\hat{p})=-(plog(\hat{p})+(1-p)log(1-\hat{p}))

推广即可得到多分类分割的交叉熵损失函数公式：

CE=-\sum_{classes}plog\hat{p}

这里要说明一下，在从二分类推广到多分类分割问题时，需要用到one-hot编码。这在语义分割任务中是一个必不可少的步骤。一般情况下，我们分割的目标是为输入图像的每个像素预测一个标签：

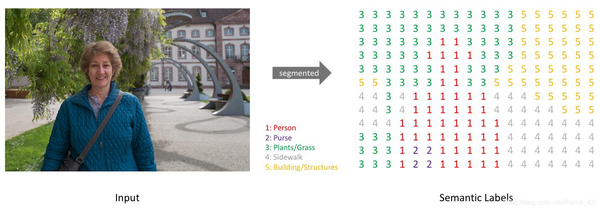
语义分割原图与分割结果对比

但是FCN类网络输出结果是hwc的特征图，想要在特征图与GT之间 计算Loss值 ，就必须进行转换使两者额的shape对应，而且每个像素点拥有对每一类的预测概率。因此，对于网络输出的特征图（假设预定类别数为C），我们使网络输出特征图为hwC,然后对每个像素位置的所有通道进行softmax操作，以使其表示为预测概率，最终通过取每个像素点在所有 channel 的 argmax 可以得到该像素点最终的预测类别。 对于数据标签（mask），为每一个类别创建一个输出通道（one-hot编码）。

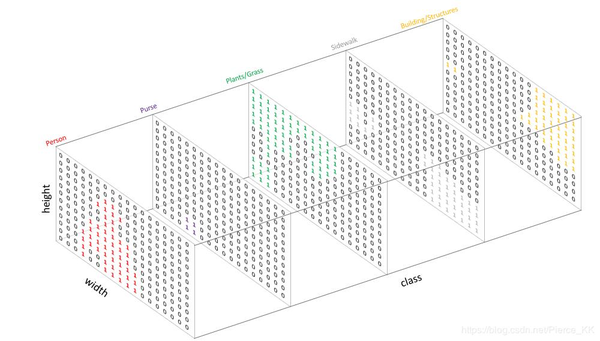
GT经过one-hot编码后

这样一来，多分类转化为各个channel的二分类问题。

小结：交叉熵损失函数行使监督、易于理解，但忽略了不同类样本（像素）在样本空间的数量比例。ont-hot编码广泛应用于图像多类别分割问题中，使得所有二分类损失函数可以间接用于多分类任务。

1.2 加权交叉熵(Weighted Cross Entorpy,WCE）

交叉熵损失分别计算每个像素的交叉熵，然后对所有像素进行平均，这意味着我们默认每类像素对损失的贡献相等。 如果各类像素在图像中的数量不平衡，则可能出现问题，因为数量最多的类别会对损失函数影响最大，从而主导训练过程。 Long等提出了为每个类加权的交叉熵损失（WCE），以抵消数据集中存在的类不平衡。以二类分割为例，WCE可被定义为：

WCE(p,\hat{p})=-(\beta plog(\hat{p})+(1-p)log(1-\hat{p}))

当 \beta>1 时，可降低FN比例，当 \beta<1 时，可降低FP比例。即想要减小哪一类的误分率，就给哪一类赋予更大的相对权值。为了同时调整负样本的权值，可以使用BCE(Balanced Cross Entropy)损失函数：

BCE(p,\hat{p})=-(\beta plog(\hat{p})+(1-\beta)(1-p)log(1-\hat{p}))

Ronnenberger等人在交叉熵函数中添加了一个距离学习距离，加强模型对类间距离的学习，以在彼此之间非常接近的情况下实现更好的分割，公式如下：

BCE(p,\hat{p})+w_0\cdot exp(-\frac{(d_1(x)+d_2(x))^2}{2\sigma ^2})

其中 d_1(x)、d_2(x) 是两个距离函数，在细胞分割问题中，Lin等用于计算当前像素到最近的和第二近细胞的边界的距离。这个损失函数是在著名的U-Net论文中提出来的。

小结：对交叉熵损失函数进行加权后，可以削弱样本类数量不平衡引起的问题。

1.3 Focal Loss

为了降低易分样本对损失函数的贡献，使模型更加专注于区分难分样本，Lin等人用难易区分权重 (1-\hat{p})^\gamma 对加权交叉熵损失函数进行进一步改进，得到Focal Loss：

FL(p,\hat{p})=-(\alpha (1-\hat{p})^\gamma plog(\hat{p})+(1-\alpha)\hat{p}^\gamma(1-p)log(1-\hat{p}))

其中 \alpha 是类数量平衡因子， \gamma 是难易分平衡因子。\alpha 越大，对应的类对损失函数的贡献就越大，对应的误分率就越低。 \gamma 越大，难分样本对损失函数的贡献越大，当 \gamma=0 时，Focal Loss等价于BCE（加权交叉熵损失）。当 \alpha=0.5,\gamma=0 时，等价于CE（交叉熵损失）。

小结：交叉熵系列损失函数发展到Focal Loss基本完备了，解决了类数量不平衡，并且动态增加了针对难分样本的权重，随着训练的进行，难分样本的权重也会慢慢降低。

总结：交叉熵系列损失函数大概就以上这几类，损失函数的改进其实相对于网络结构的改进要难一些，有些具体的问题可以利用一些先验来对损失函数做正则化（例如U-Net的损失函数），主体部分用Focal Loss就可以。

2. 基于重合度度量的损失函数

首先需要说明一下重合度如何度量，最常用的评价指标是IoU(交并比）：

IoU=\frac{TP}{TP+FP+FN}=\frac{|X \cap Y|}{|X|+|Y|-|X \cap Y|}

其中X和Y分别表示预测结果和GroundTruth，这是最直观地表示预测结果与标签mask之间重合度的指标。取值范围为[0~1]，越大表明分割结果越接近GT。所以我们可以基于此来设计损失函数，那么评价指标和损失函数更相似，分割效果会不会更好？

2.1 Dice Loss（DL）

首先需要了解Dice系数，它可以衡量两个样本之间重叠程度，与F1-Score等价，与IoU基本相似。表达式为：

DC=\frac{2TP}{2TP+FP+FN}=\frac{2|X \cap Y|}{|X|+|Y|}

相当于在IoU的分子分母上分别加了一个 |X \cap Y| ，那么 DC\geq IoU ,取值范围和IoU类似为[0,1]。基于此来设计Dice Loss可以表示为：

DL=1-\frac{2|X \cap Y|}{|X|+|Y|}=1-\frac{2<p,\hat{p}>}{||p||_1+\left| |\hat{p}| \right|_1}

分割性能越好，则DC的值越低。其中 <p,\hat{p}> 表示每个通道的GT与预测结果矩阵点乘， 可以有效地将预测中未在 target mask 中“激活”的所有像素清零。对于剩余的像素，主要是在惩罚低置信度预测；||\cdot||_1 表示一范数，即矩阵元素绝对值之和，为简化计算，也可以用2范数代替。Dice Loss在2016年的V-Net中首次提出，非常适用于类别不平衡问题，本身可以有效抑制类别不平衡引起的问题。

2.2 Tversky Loss（TL）

Tversky Loss是对Dice Loss的正则化版本，为控制FP和FN对损失函数的贡献，TL对它们进行了加权：

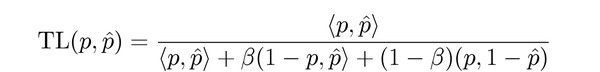
当beta=0.5时，TL等价于DL。

2.3 指数对数损失（Exponential Logarithmic Loss）

Wong提出了一种使用指数对数Dice Loss（ L_{eld} ）和加权指数交叉熵损失（ Lwece ）的加权和构成的损失函数，以提高小结构的分割精度，这些要分割的小结构对象的大小一般存在较大差异。

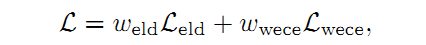
其中：

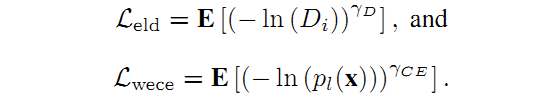
x,i 和l 分别表示像素位置，预测标签和数据真实标签（GT）。 D_i 表示平滑Dice Loss（在Dice Loss的分子分母上分别加1，可以避免出现除零问题）。 \gamma _D 和\gamma _{CE} 用于控制两部分损失函数的非线性。

2.4 Lovasz-Softmax Loss（LSL）

已知Jaccard损失（IoU损失）是submodular（子模，这部分还不太理解），因此Berman等人提出使用Lovasz铰链和Jaccard损失进行二值分割，并提出了Jaccard损失的替代品，称为Lovasz-Softmax损失， 适用于多类别分割任务。 因此，Lovasz-Softmax损失是离散Jaccard损失的平滑扩展，定义为：

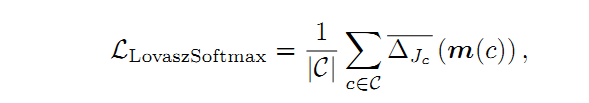
其中 \Delta_{J_{c}}(\cdot) 表示子模Jaccard损失的凸闭包，表示它是紧的凸闭包且多项式时间可计算，C表示所有类别， J_c 和 m(c) 表示Jaccard索引和C个类别的向量误差。

2.5 边界损失（Boundary Loss，BL）

Kervadec提出了一种新的损失函数：

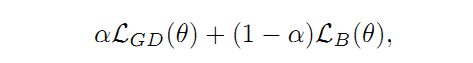
其中，第一部分是正则化后的Dice Loss：

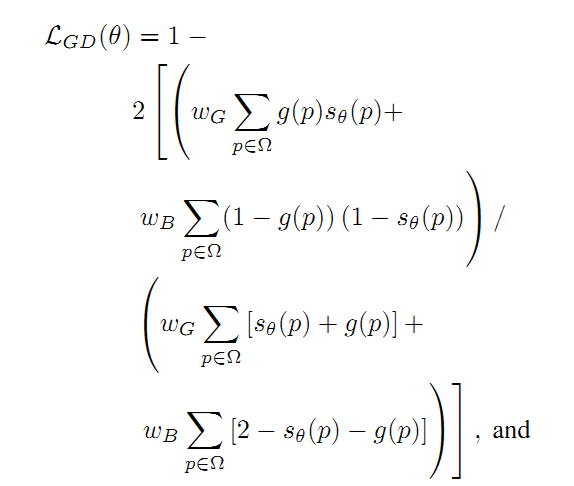
第二部分是边界损失（Boundary Loss）：

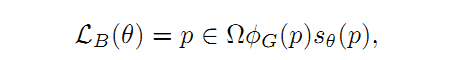
两部分用 \alpha 来调整相对大小。具体参数含义如下：

2.6 保守损失（Conservative Loss，CL）

这个损失函数的作用和它的名字一样保守：通过惩罚极端情况并鼓励中等情况来在域适应任务中实现良好的泛化能力。CL可以表示为： CL(p_t)=\lambda(1+log_a (p_t))^2*log_a(-log_a(p_t))\

其中 P_t 是对标签的预测概率， a 是对数的底数， a 和 \lambda 分别选择为e（欧拉数）和5。

2.7 小结

​ 其他类似的工作还包括优化分割指标的方法，加权损失函数以及向损失函数添加正则化项以编码几何和拓扑形状先验的方法。以上介绍的这些方法可以直接拿来使用，也可以针对自己的具体问题，添加权重或正则化来改进。

3. 总结

​ 图像分割（尤其是医学图像）中的一个重要问题是要克服类别不平衡问题，基于重叠度量的方法在克服不平衡方面表现出相当好的性能。 在下一篇总结中，我们总结一下用于医学图像分割任务的新损失函数或上述（修改后的）损失函数。

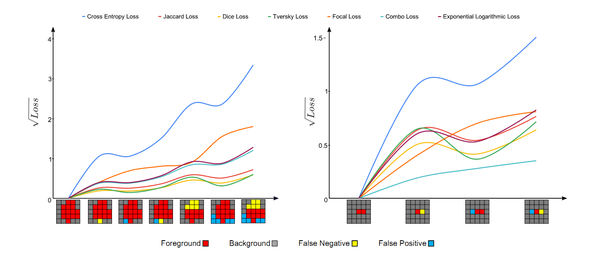
不同损失函数针对大/小对象分割的效果对比

上图将不同损失函数的表现进行了可视化（分别为分割大型和小型对象）。 对于损失函数的参数，我们使用与作者在各自论文中所设置的参数。

对于上面两张图，每张图底部的可视化分割结果，从左向右，预测结果和GroundTruth的重叠逐渐变小，即产生更多的假阳性（FP）和假阴性（FN）。 理想情况下，Loss函数的值应随着预测更多的假阳性和假阴性而单调增加。 对于大型对象（左图），几乎所有现象都遵循此假设； 但是，对于小型对象（右图），只有combo loss和focal loss会因较大的误差而单调增大更多。 换句话说，在分割大/小对象时，基于重合度（重叠度）的损失函数波动很大，这导致优化过程的不稳定。 使用交叉熵作为基础的损失函数和重叠度作为加权正则函数的损失（combo loss）函数在训练过程中显示出更高的稳定性。（combo loss属于医学图像分割问题中提出来的损失函数，所以放到下一篇《基于医学图像的自然图像和医学图像分割：损失函数设计（二）》中介绍。）