D. Karen and Test(Round419)
Karen has just arrived at school, and she has a math test today!

The test is about basic addition and subtraction. Unfortunately, the teachers were too busy writing tasks for Codeforces rounds, and had no time to make an actual test. So, they just put one question in the test that is worth all the points.
There are n integers written on a row. Karen must alternately add and subtract each pair of adjacent integers, and write down the sums or differences on the next row. She must repeat this process on the values on the next row, and so on, until only one integer remains. The first operation should be addition.
Note that, if she ended the previous row by adding the integers, she should start the next row by subtracting, and vice versa.
The teachers will simply look at the last integer, and then if it is correct, Karen gets a perfect score, otherwise, she gets a zero for the test.
Karen has studied well for this test, but she is scared that she might make a mistake somewhere and it will cause her final answer to be wrong. If the process is followed, what number can she expect to be written on the last row?
Since this number can be quite large, output only the non-negative remainder after dividing it by 109 + 7.
The first line of input contains a single integer n (1 ≤ n ≤ 200000), the number of numbers written on the first row.
The next line contains n integers. Specifically, the i-th one among these is ai (1 ≤ ai ≤ 109), the i-th number on the first row.
Output a single integer on a line by itself, the number on the final row after performing the process above.
Since this number can be quite large, print only the non-negative remainder after dividing it by 109 + 7.
5
3 6 9 12 15
36
4
3 7 5 2
1000000006
In the first test case, the numbers written on the first row are 3, 6, 9, 12 and 15.
Karen performs the operations as follows:
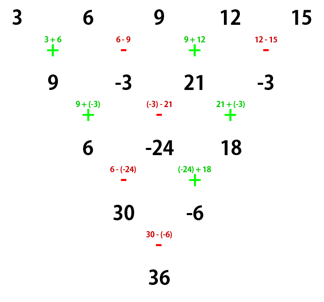
The non-negative remainder after dividing the final number by 109 + 7 is still 36, so this is the correct output.
In the second test case, the numbers written on the first row are 3, 7, 5 and 2.
Karen performs the operations as follows:
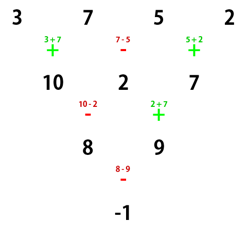
The non-negative remainder after dividing the final number by 109 + 7 is 109 + 6, so this is the correct output.
hint:神奇的数学公式。。。
这种规律题。。。确实很伤脑子。。。
多写几组数可以发现规律,当n为奇数的时候和当n为偶数的时候,还要留意下他们的系数
#include <iostream> #include <cstring> #include <string> #include <queue> #include <vector> #include <map> #include <set> #include <cmath> #include <cstdio> #include <algorithm> #include <functional> #define LL long long #define N 200010 #define inf 0x3f3f3f3f using namespace std; const LL mod = 1e9 + 7; const double eps = 1e-9; LL num[N]; LL fac[N] = { 1,1 }; LL inv[N] = { 0,1 }; LL f[N] = { 1,1 }; LL C(LL n, LL i) { if (i == 0 || i == n) return 1; return fac[n] * inv[n - i] % mod * inv[i] % mod; } void init(){ for (int i = 2; i<N; i++){ fac[i] = fac[i - 1] * i % mod; f[i] = (mod - mod / i) * f[mod%i] % mod; inv[i] = inv[i - 1] * f[i] % mod; } } int main() { cin.sync_with_stdio(false); LL n, ans; init(); while (cin >> n) { for (int i = 1; i <= n; i++) { cin >> num[i]; } if (n == 1) { cout << num[1] << endl; } else if (n <= 2) { cout << (num[2] + num[1]) % mod << endl; } else { ans = 0; if (n % 2) { n--; for (int i = 1; i <= n; i++) { if (ans % 2) { num[i] -= num[i + 1]; } else { num[i] += num[i + 1]; } ans++; num[i] = (num[i] + mod) % mod; } } ans = 0; LL temp; int ope = (n % 4 == 0 ? -1 : 1); for (int i = 1; i <= n; i += 2) { temp = C(n / 2 - 1, i / 2); ans += temp*(num[i] + ope*num[i + 1]) % mod; ans %= mod; } ans = (ans%mod + mod) % mod; cout << ans << endl; } } return 0; }


 浙公网安备 33010602011771号
浙公网安备 33010602011771号