C. Karen and Game(Round419)

C. Karen and Game

time limit per test

2 seconds

memory limit per test

512 megabytes

input

standard input

output

standard output

On the way to school, Karen became fixated on the puzzle game on her phone!

The game is played as follows. In each level, you have a grid with n rows and m columns. Each cell originally contains the number 0.

One move consists of choosing one row or column, and adding 1 to all of the cells in that row or column.

To win the level, after all the moves, the number in the cell at the i-th row and j-th column should be equal to gi, j.

Karen is stuck on one level, and wants to know a way to beat this level using the minimum number of moves. Please, help her with this task!

Input

The first line of input contains two integers, n and m (1 ≤ n, m ≤ 100), the number of rows and the number of columns in the grid, respectively.

The next n lines each contain m integers. In particular, the j-th integer in the i-th of these rows contains gi, j (0 ≤ gi, j ≤ 500).

Output

If there is an error and it is actually not possible to beat the level, output a single integer -1.

Otherwise, on the first line, output a single integer k, the minimum number of moves necessary to beat the level.

The next k lines should each contain one of the following, describing the moves in the order they must be done:

• row x, (1 ≤ x ≤ n) describing a move of the form "choose the x-th row".
• col x, (1 ≤ x ≤ m) describing a move of the form "choose the x-th column".

If there are multiple optimal solutions, output any one of them.

Examples

input

3 5
2 2 2 3 2
0 0 0 1 0
1 1 1 2 1

output

4
row 1
row 1
col 4
row 3

input

3 3
0 0 0
0 1 0
0 0 0

output

-1

input

3 3
1 1 1
1 1 1
1 1 1

output

3
row 1
row 2
row 3

Note

In the first test case, Karen has a grid with 3 rows and 5 columns. She can perform the following 4 moves to beat the level:

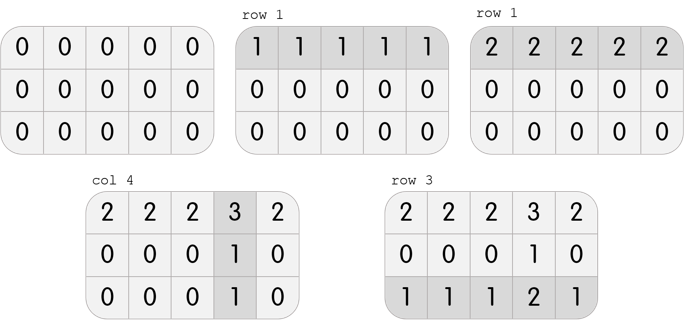
In the second test case, Karen has a grid with 3 rows and 3 columns. It is clear that it is impossible to beat the level; performing any move will create three 1s on the grid, but it is required to only have one 1 in the center.

In the third test case, Karen has a grid with 3 rows and 3 columns. She can perform the following 3 moves to beat the level:

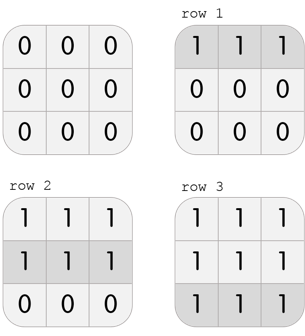
Note that this is not the only solution; another solution, among others, is col 1, col 2, col 3.

hint:给你一个矩阵，问你能不能通过一些操作把这个矩阵变成全0矩阵

这个题目有2s，并且数据也不大。。。

直接暴力加贪心就可以了

我们先判断行和列的大小，从小的开始处理，例如，有10行5列的话，明显从列开始的话，答案更优

确定从哪里开始之后，我们就开始扫描每行或列，减去该行（列）中最小的元素，若此时矩阵不为0，则再从列（行）开始减，用row, col两个数组记录答案

最后输出即可

#include<iostream>
#include<cstdio>
#include<string>
using namespace std;
#define FOR(i, a, b) for(int i=a; i<b; i++)
#define FO(i, a, b) for(int i=a; i<=b; i++)
int str[240];
int a[120][120];
int n, m, i, j, cnt = 0;

//模拟题。。。观察思考规律，每行每列减去最小的元素，如果最后得不到全 0 矩阵则失败（逆向思维，从所给矩阵减去一定数得到全0矩阵） ---
//有一个坑点，如果列数小于行数，则先从列开始减，否则从行开始减
int main(){
    scanf("%d%d", &n, &m);
    FOR(i, 0, n){
        FOR(j, 0, m){
            scanf("%d", &a[i][j]);
        }
    }
    if(n <= m){
    FOR(i, 0, n){
        int Min=600;
        FOR(j, 0, m){
            if(a[i][j] < Min) Min = a[i][j];
        }
        if(Min){
            FOR(k, 0, m){
                a[i][k] -= Min;
            }
            str[i] = Min;
            cnt += Min;
        }
    }
    FOR(i, 0, m){
        int Min=600;
        FOR(j, 0, n){
            if(a[j][i] < Min) Min = a[j][i];
        }
        if(Min){
            FOR(k, 0, n){
                a[k][i] -= Min;
            }
            str[100 + i] = Min;
            cnt += Min;
        }
    }
    }
    else{
        FOR(i, 0, m){
        int Min=600;
        FOR(j, 0, n){
            if(a[j][i] < Min) Min = a[j][i];
        }
        if(Min){
            FOR(k, 0, n){
                a[k][i] -= Min;
            }
            str[100 + i] = Min;
            cnt += Min;
        }
        }
        FOR(i, 0, n){
        int Min=600;
        FOR(j, 0, m){
            if(a[i][j] < Min) Min = a[i][j];
        }
        if(Min){
            FOR(k, 0, m){
                a[i][k] -= Min;
            }
            str[i] = Min;
            cnt += Min;
        }
    }
    }
//    FOR(i, 0, n){
//        FOR(j, 0, m){
//            printf("%d ", a[i][j]);
//        }
//        printf("\n");
//    }
    int flag=1;
    FOR(i, 0, n){
        if(!flag) break;
        FOR(j, 0, m){
            if(a[i][j] != 0){
                flag=0;
                break;
            }
        }
    }
    if(!flag){
        printf("-1\n");
    }
    else{
        printf("%d\n", cnt);
        FOR(i, 0, 100){
            if(str[i] != 0){
                while(str[i]--){
                    printf("row %d\n", i + 1);
                    cnt++;
                }
            }
        }
        FOR(i, 100, 200){
            if(str[i] != 0){
                while(str[i]--){
                    printf("col %d\n", i + 1 - 100);
                    cnt++;
                }
            }
        }
    }
    return 0;
}