D. An overnight dance in discotheque（Round4 418）

D. An overnight dance in discotheque

time limit per test

2 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

The crowdedness of the discotheque would never stop our friends from having fun, but a bit more spaciousness won't hurt, will it?

The discotheque can be seen as an infinite xy-plane, in which there are a total of n dancers. Once someone starts moving around, they will move only inside their own movement range, which is a circular area Ci described by a center (xi, yi) and a radius ri. No two ranges' borders have more than one common point, that is for every pair (i, j) (1 ≤ i < j ≤ n) either ranges Ci and Cj are disjoint, or one of them is a subset of the other. Note that it's possible that two ranges' borders share a single common point, but no two dancers have exactly the same ranges.

Tsukihi, being one of them, defines the spaciousness to be the area covered by an odd number of movement ranges of dancers who are moving. An example is shown below, with shaded regions representing the spaciousness if everyone moves at the same time.

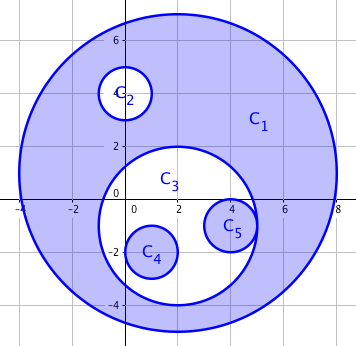
But no one keeps moving for the whole night after all, so the whole night's time is divided into two halves — before midnight and after midnight. Every dancer moves around in one half, while sitting down with friends in the other. The spaciousness of two halves are calculated separately and their sum should, of course, be as large as possible. The following figure shows an optimal solution to the example above.

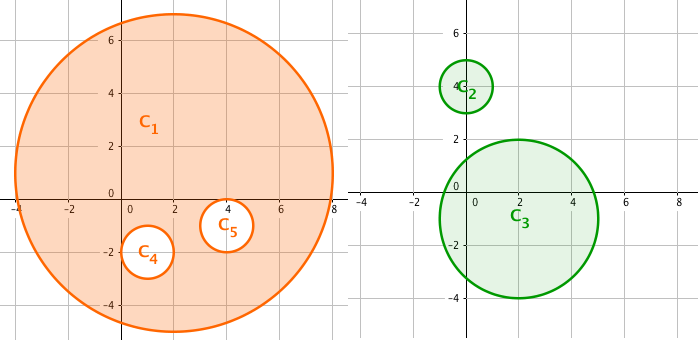
By different plans of who dances in the first half and who does in the other, different sums of spaciousness over two halves are achieved. You are to find the largest achievable value of this sum.

Input

The first line of input contains a positive integer n (1 ≤ n ≤ 1 000) — the number of dancers.

The following n lines each describes a dancer: the i-th line among them contains three space-separated integers xi, yi and ri ( - 106 ≤ xi, yi ≤ 106, 1 ≤ ri ≤ 106), describing a circular movement range centered at (xi, yi) with radius ri.

Output

Output one decimal number — the largest achievable sum of spaciousness over two halves of the night.

The output is considered correct if it has a relative or absolute error of at most 10 - 9. Formally, let your answer be a, and the jury's answer be b. Your answer is considered correct if .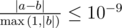

Examples

input

5
2 1 6
0 4 1
2 -1 3
1 -2 1
4 -1 1

output

138.23007676

input

8
0 0 1
0 0 2
0 0 3
0 0 4
0 0 5
0 0 6
0 0 7
0 0 8

output

289.02652413

Note

The first sample corresponds to the illustrations in the legend.

 hint：给n个圆的圆心坐标和半径，进行如下操作，加上奇数个圆覆盖的面积，减去被偶数个圆覆盖的面积。如果仅仅是这样的话，就没有必要求最大值了，所以题目给了一个条件可以用两个坐标系来表示这些圆，怎么分配才能使得面积最大呢？

在网上看到一个比较玄的做法---找规律：首先最大的圆（不被任何圆包含的圆）我们肯定要加上；然后考虑被一个圆包围的圆，我们可以将它拿出去，也可以不拿出去：接下来考虑呗两个圆包含的圆。。。这样下去我们就找到规律了。。。把只被一个圆包围的圆拿出去，其他圆不变。然后就是++-+-的操作了（这种做法感觉还是要看运气啊）

//看成一个树形结构，我办不到啊。。。
//找规律贪心。。。感觉还是比较难想到
//学到了一个黑科技。。。 --- hypot（ a , b ）（包含在头文件cmath中，用来计算直角三角形的斜边）
#include<iostream>
#include<cstdio>
#include<cmath>
using namespace std;
#define pi acos(-1.0)
struct node{
    double x, y, r;
    int num;
}area[1050];
int cal(int i, int j){
    double d = hypot(area[i].x - area[j].x, area[i].y - area[j].y);
    if(area[j].r - area[i].r >= d) return 1;
    else return 0;
}
int main(){
    int n;
    scanf("%d", &n);
    for(int i=0; i<n; i++){
        scanf("%lf%lf%lf", &area[i].x, &area[i].y, &area[i].r);
    }
    for(int i=0; i<n; i++){
        for(int j=0; j<n; j++){
            if(i != j){
                if(cal(i, j)) area[i].num++;
            }
        }
    }
    double ans = 0;
    for(int i=0; i<n; i++){
        if(area[i].num==0 || area[i].num==1) ans += pi*area[i].r*area[i].r;
        else if(area[i].num % 2 == 1) ans += pi*area[i].r*area[i].r;
        else ans -= pi*area[i].r*area[i].r;
    }
    printf("%.12lf\n", ans);
    return 0;
}

介绍另一种方法：树形dp（暂时还没搞出来。。。占个坑）