任意1-10中的4个数字，使用加减乘除计算得出24结果的可能组合（C#版），很多人小时候都玩过

目录

1. 需求；
2. 需求该如何分析呢，怎么划分成小需求呢？
3. 如何把小需求编排成完整需求；

学有所得

1. 学会分析需求，由哪些组成（规则，逻辑等）;
2. 能把的需求分解成很多子需求、或孙需求、或童孙需求，直到每个需求很清晰可实施地为止
3. 学会把各种子孙需求，通过组合编排，最终成为一个完整的大需求解决方案

需求

需求：任意1-10中的4个数字，使用加减乘除计算得出24结果的可能组合；
通过初步分析，我们可以得到如下规则：
规则：1、任意1-10中的4个数字；
2、使用加减乘除计算得出24;

3、在任何一次计算中不能出现小数，
比如：(4.0 + 8.0) / (3.0 / 6.0) = 24.0，这种是不算的，虽然最终结果是24，因为3/6=0.5
(8.0 / 3.0) * (4.0 + 5.0) = 24.0，虽然最终为24，但是在第一步结果却是小数，所以不成立；

 

4、整个运算中应该使用double类型，因为整数相除，使用int类型，在计算机中，会把余数抹掉，直接取整，这样就会造成结果不正确；

那需求该如何分析呢，怎么划分成小需求呢？

一般来说我们都会通过案例来分析，比如：这个需求，我们使用传统的计算，假设我们已经有这四个数[3,4,8,6],可能会有如下组合:

方案：((4.0 + 8.0) * 6.0) / 3.0=24.0;
方案：((3.0 * 4.0) - 8.0) * 6.0=24.0;
方案：((8.0 - 6.0) * 3.0) * 4.0=24.0;
方案：((4.0 + 8.0) / 3.0) * 6.0=24.0;

方案：(4.0 * 3.0) * (8.0 - 6.0) = 24.0;
方案：(6.0 / 3.0) * (4.0 + 8.0) = 24.0；

我们暂时先分析这个几个方案，大家看到这里，可以先思考一下有什么规律，有什么规则；

....................................................................................................Thinking..............................

从这些方案中，我们可以得出如下蹊跷之处：
1、所有的方案中，都在这四个数的所有可能排列组合中（我记忆之中，应该是高中数学的知识点）；
2、我们可以把计算法则归纳为两种，所有的都可以归纳到一下两种中去；
第一、从左到右的依次计算；
第二、两两组合，前两个数计算结果和后两个数的计算结果再次计算；
第三、每个方案都有3个运算符；

不知道大家是不是和我发现的一样不，或者说有更多的发现；我认为不管什么发现都可以先列出来，然后在逐个去去除一些太离谱的发现；
我们再继续顺藤摸瓜，到此我们可以把需求分解如下：

我们继续分析需求，看看是否可以再次分解

从上面的需求中我们可以进一步进行分解

第一、如何获取四个数的所有排列组合？
1、举例，我们继续使用案列来分析，比如 [3,4,8,6]
[3,4,8,6]（基准）
[4,3,8,6]（第二和第一调换）
[3,8,4,6] [8,3,4,6]（第三和第二调换，第二和第一调换）
[3,4,6,8] [3,6,4,8] [6,3,4,8] （第四和第三调换， 第三和第二调换，第二和第一调换）
这样是不是所有的排列组合呢?显然不是？因为还有三种基准进行上面的排列组合，也就是上面每行最后一列
[4,3,8,6]（基准2）
[8,3,4,6]（基准3）
[6,3,4,8]（基准4）
2、通过上面的举例，我们就可以先获取所有的基准组合；
3、通过上面，我们可以知道每种基准的所有组合；
4、通过上面的方法获取的组合会有重复，需要前需要去重；
这样我们就能获取4个数的所有排列组合；我感觉这种获取所有排列组合的算法很笨重（有没有感觉有点想冒泡排序），不优雅，肯定有更优的方案，只是我不知道而已，如果知道的可以留言，谢谢；
所有排列分析到此，是不是还需要继续分析，可以继续思考；本人感觉可以落地了；如果觉得需要继续分析的，可以继续分解，知道自己很清晰，知道怎么干为止（这个因人而异）；请看代码；

获取所有基准代码：

 List<double[]> resultAllList = new List<double[]>();
            List<double[]> list = new List<double[]>();
            list.Add(array);
            list.Add(new double[] { array[1], array[2], array[3], array[0] });
            list.Add(new double[] { array[2], array[3], array[0], array[1] });
            list.Add(new double[] { array[3], array[0], array[1], array[2] });

 

获取每个基准的所有排列组合：

    /// <summary>
        /// 获取array的所有可能组合
        /// </summary>
        /// <param name="list"></param>
        /// <param name="array"></param>
        public static void GetAllArray(List<double[]> list, double[] array)
        {
            if (!Exists(list, array))
            {
                list.Add(array);
            }

            for (int i = 1; i < 4; i++)
            {
                double[] arrayCopy = DeepCopyByBin<double[]>(array);
                List<double[]> newList = GetArrayList(arrayCopy, i);
                newList.ForEach((item) =>
                {
                    if (!Exists(list, item))
                    {
                        list.Add(item);
                    }
                });

            }
        }

        /// <summary>
        /// 获取array下标遇到i的位置左右组合
        /// </summary>
        /// <param name="array"></param>
        /// <param name="i"></param>
        /// <returns></returns>
        public static List<double[]> GetArrayList(double[] array, int i)
        {
            List<double[]> list = new List<double[]>();

            for (int j = i; j > 0; j--)
            {
                double temp = array[j];
                array[j] = array[j - 1];
                array[j - 1] = temp;
                list.Add(array);
                array = DeepCopyByBin<double[]>(array);
            }

            return list;
        }

        /// <summary>
        /// array是否存啊在list中
        /// </summary>
        /// <param name="list"></param>
        /// <param name="array"></param>
        /// <returns></returns>
        public static bool Exists(List<double[]> list, double[] array)
        {
            bool isExist = false;
            for (int i = 0; i < list.Count; i++)
            {
                var item = list[i];
                if (item[0] == array[0] && item[1] == array[1] && item[2] == array[2] && item[3] == array[3])
                {
                    isExist = true;
                    break;
                }
            }
           
            return isExist;

        }

 

第二，对于算法法则该如何继续分析呢?我们可以继续使用举例
从上面随意获取一种排列组合，比如：[3,4,8,6]
1、从左到右的组合，在上面四个数字中，任意两个数中，我们可以有+，- ，*，/这四种算法，这又是一种计算的所有排列组合，并把结果和24对比，如果相等，那就是可行方案；
那我们是不是继续使用上面获取组合的方式呢？显然不是，这里关键点在于：任意两个数中都有+-*/的算法，这里我们可以使用三个for循环解决；
举例：((3.0 * 4.0) - 8.0) * 6.0=24.0;

    /// <summary>
        /// 计算array能算24点的所有组合，从左到右的顺序
        /// </summary>
        /// <param name="array"></param>
        /// <returns></returns>
        public static int Caculate24Point(double[] array)
        {
            int count = 0;
            if (array.Length != 4)
            {
                throw new Exception("不是四个数");
            }


            for (int i = 0; i < operators.Length; i++)
            {
                string op = operators[i];

                String expressionStr = "";

                double result = GetTwoNumCaculate(array[0], array[1], op);
                if (!IsValidResult(result))
                {
                    continue;
                }
                expressionStr = $"({array[0]}{op}{array[1]})";

                for (int j = 0; j < operators.Length; j++)
                {
                    string op2 = operators[j];

                    double result1 = GetTwoNumCaculate(result, array[2], op2);
                    if (!IsValidResult(result1))
                    {
                        continue;
                    }
                    String expressionStr2 = $"({expressionStr}{op2}{array[2]})";
                    for (int k = 0; k < operators.Length; k++)
                    {
                        string op3 = operators[k];


                        double result2 = GetTwoNumCaculate(result1, array[3], op3);
                        String expressionStr3 = $"{expressionStr2}{op3}{array[3]}";//String.format("%s %s %s", expressionStr2, op3, array[3]);

                        if (result2 == 24.0d)
                        {
                            count++;
                            Console.WriteLine($"方案：{expressionStr3}={result2}");

                        }
                    }
                }
            }
            return count;
        }

 

2、两两组合，思路和上面有些相似，

前两个数的任意计算结果1，
后两个数的任意计算结果2，
结果1和结果2的任意计算结果3，
结果3和24对比，如果相等，那就是可行方案；
举例：(3.0 * 4.0) * (8.0 - 6.0) = 24.0;

 /// <summary>
        /// 计算array能算24点的所有组合 ,两两组合
        /// </summary>
        /// <param name="array"></param>
        /// <returns></returns>
        public static int Caculate24Point2(double[] array)
        {
            int count = 0;
            if (array.Length != 4)
            {
                throw new Exception("不是四个数");
            }
            for (int i = 0; i < operators.Length; i++)
            {
                string op = operators[i];
                double result1 = GetTwoNumCaculate(array[0], array[1], op);
                if (!IsValidResult(result1))
                {
                    continue;
                }
                String expressionStr1 = $"({array[0]}{op}{array[1]})";
                for (int j = 0; j < operators.Length; j++)
                {
                    string op2 = operators[j];
                    double result2 = GetTwoNumCaculate(array[2], array[3], op2);
                    if (!IsValidResult(result2))
                    {
                        continue;
                    }
                    String expressionStr2 = $"({array[2]}{op2}{array[3]})";
                    for (int k = 0; k < operators.Length; k++)
                    {
                        string op3 = operators[k];

                        double result3 = GetTwoNumCaculate(result1, result2, op3);
                        String expressionStr3 = $"{expressionStr1} {op3} {expressionStr2}";
                        if (result3 == 24.0d)
                        {
                            count++;
                            Console.WriteLine($"方案： {expressionStr3} = {result3}");

                        }
                    }
                }

            }
            return count;
        }

 

某一种四个数的所有运算排列通过上面的方式我们可以全部获取，分析到此，我觉得代码可以落地，当然，如果你觉得还不够清晰，可以继续分析，直到自己清晰为止，这里我只是提供分解需求的思路而已；在软件工程中，我们必定先分析需求，然后分解需求，我们有四色分析方式，我们还有DDD领域的分析方式等，都是需要通过逐步分解成更小的需求来反复验证的；

 

到目前为止我们可以得出如下思维导图

 

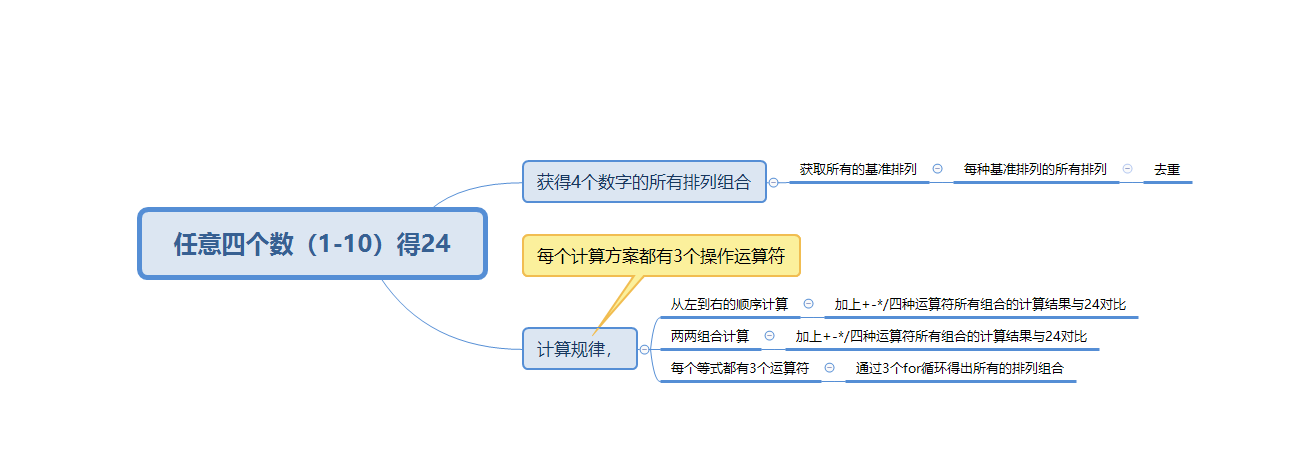
把各种子孙需求，通过组合编排，最终成为一个完整的大需求解决方案

最后，我们把每个小的需求加上一些规则逻辑组合成完整的大需求，我们暂时叫做编排吧；
这里其实也是一个难点，很多人希望一次性把代码写完整，写正确，其实这种思路是不正确的，这样只会增加代码的难度，一次性能把代码写的有多完整多正确，这个跟每个人的编程经验熟练度有关；
不管编程多牛，从无到有的敲代码方向不是一次性把所有的代码完成，重点方向把核心逻辑思路编写上，其次才逐步把一些细节逻辑规则加上去，这个就和我们小时候学画画一样，画一颗树先画主干然后画叶子最后添加果子和花之类的；

 

到目前为止是否完整呢？其实还差一点，任意的1-10的数字从哪里获取，不过需求没有明确，可以是用户输入，数据库获取，其他接口的传入，我们这里就定位用户输入吧

获取用户输入代码如下：

double[] array = new double[4];
            int index = 0;
            while (index < 4)
            {
                Console.WriteLine(String.Format("请输入第{0}个1-10的整数", index + 1));
                String tempNumStr = Console.ReadLine();
                if (!int.TryParse(tempNumStr, out int tmpNum))
                {
                    Console.WriteLine("你输入的不是一个整数");
                    continue;
                }

                if (tmpNum < 0 || tmpNum > 10)
                {
                    Console.WriteLine("你输入的数字不是1-10的数字");
                    continue;
                }

                array[index++] = (double)tmpNum;

            }

            Console.WriteLine($"你输入的4个1-10的整数为{array[0]},{array[1]},{array[2]},{array[3]}");

 

 

最终完整代码如下：

using System;
using System.Collections.Generic;
using System.IO;
using System.Linq;
using System.Runtime.Serialization.Formatters.Binary;
using System.Text;
using System.Threading.Tasks;

namespace Point24Caculate
{
    class Program
    {
        private static string[] operators = new string[] { "+", "-", "*", "/" };


        static void Main(string[] args)
        {
            double[] array = new double[4];
            int index = 0;
            while (index < 4)
            {
                Console.WriteLine(String.Format("请输入第{0}个1-10的整数", index + 1));
                String tempNumStr = Console.ReadLine();
                if (!int.TryParse(tempNumStr, out int tmpNum))
                {
                    Console.WriteLine("你输入的不是一个整数");
                    continue;
                }

                if (tmpNum < 0 || tmpNum > 10)
                {
                    Console.WriteLine("你输入的数字不是1-10的数字");
                    continue;
                }

                array[index++] = (double)tmpNum;

            }

            Console.WriteLine($"你输入的4个1-10的整数为{array[0]},{array[1]},{array[2]},{array[3]}");
            Console.WriteLine("结果如下：");

            List<double[]> resultAllList = new List<double[]>();
            List<double[]> list = new List<double[]>();
            list.Add(array);
            list.Add(new double[] { array[1], array[2], array[3], array[0] });
            list.Add(new double[] { array[2], array[3], array[0], array[1] });
            list.Add(new double[] { array[3], array[0], array[1], array[2] });
            for (int i = 0; i < list.Count; i++)
            {
                GetAllArray(resultAllList, DeepCopyByBin(list[i]));
            }

            int sum = 0;
            resultAllList.ForEach(itemArray =>
            {
                
                sum += Caculate24Point(itemArray);
                sum += Caculate24Point2(itemArray);
            });


            Console.WriteLine("总共方案数量：" + sum);

            Console.ReadLine();
        }

        /// <summary>
        /// 获取array的所有可能组合
        /// </summary>
        /// <param name="list"></param>
        /// <param name="array"></param>
        public static void GetAllArray(List<double[]> list, double[] array)
        {
            if (!Exists(list, array))
            {
                list.Add(array);
            }

            for (int i = 1; i < 4; i++)
            {
                double[] arrayCopy = DeepCopyByBin<double[]>(array);
                List<double[]> newList = GetArrayList(arrayCopy, i);
                newList.ForEach((item) =>
                {
                    if (!Exists(list, item))
                    {
                        list.Add(item);
                    }
                });

            }
        }

        /// <summary>
        /// 获取array下标遇到i的位置左右组合
        /// </summary>
        /// <param name="array"></param>
        /// <param name="i"></param>
        /// <returns></returns>
        public static List<double[]> GetArrayList(double[] array, int i)
        {
            List<double[]> list = new List<double[]>();

            for (int j = i; j > 0; j--)
            {
                double temp = array[j];
                array[j] = array[j - 1];
                array[j - 1] = temp;
                list.Add(array);
                array = DeepCopyByBin<double[]>(array);
            }

            return list;
        }

        /// <summary>
        /// array是否存啊在list中
        /// </summary>
        /// <param name="list"></param>
        /// <param name="array"></param>
        /// <returns></returns>
        public static bool Exists(List<double[]> list, double[] array)
        {
            bool isExist = false;
            for (int i = 0; i < list.Count; i++)
            {
                var item = list[i];
                if (item[0] == array[0] && item[1] == array[1] && item[2] == array[2] && item[3] == array[3])
                {
                    isExist = true;
                    break;
                }
            }
           
            return isExist;

        }
        /// <summary>
        /// 深拷贝
        /// </summary>
        /// <typeparam name="T"></typeparam>
        /// <param name="obj"></param>
        /// <returns></returns>
        public static T DeepCopyByBin<T>(T obj)
        {
            object retval;
            using (MemoryStream ms = new MemoryStream())
            {
                BinaryFormatter bf = new BinaryFormatter();
                //序列化成流
                bf.Serialize(ms, obj);
                ms.Seek(0, SeekOrigin.Begin);
                //反序列化成对象
                retval = bf.Deserialize(ms);
                ms.Close();
            }
            return (T)retval;
        }
        /// <summary>
        /// 计算array能算24点的所有组合，从左到右的顺序
        /// </summary>
        /// <param name="array"></param>
        /// <returns></returns>
        public static int Caculate24Point(double[] array)
        {
            int count = 0;
            if (array.Length != 4)
            {
                throw new Exception("不是四个数");
            }


            for (int i = 0; i < operators.Length; i++)
            {
                string op = operators[i];

                String expressionStr = "";

                double result = GetTwoNumCaculate(array[0], array[1], op);
                if (!IsValidResult(result))
                {
                    continue;
                }
                expressionStr = $"({array[0]}{op}{array[1]})";

                for (int j = 0; j < operators.Length; j++)
                {
                    string op2 = operators[j];

                    double result1 = GetTwoNumCaculate(result, array[2], op2);
                    if (!IsValidResult(result1))
                    {
                        continue;
                    }
                    String expressionStr2 = $"({expressionStr}{op2}{array[2]})";
                    for (int k = 0; k < operators.Length; k++)
                    {
                        string op3 = operators[k];


                        double result2 = GetTwoNumCaculate(result1, array[3], op3);
                        String expressionStr3 = $"{expressionStr2}{op3}{array[3]}";//String.format("%s %s %s", expressionStr2, op3, array[3]);

                        if (result2 == 24.0d)
                        {
                            count++;
                            Console.WriteLine($"方案：{expressionStr3}={result2}");

                        }
                    }
                }
            }
            return count;
        }


        /// <summary>
        /// 计算array能算24点的所有组合 ,两两组合
        /// </summary>
        /// <param name="array"></param>
        /// <returns></returns>
        public static int Caculate24Point2(double[] array)
        {
            int count = 0;
            if (array.Length != 4)
            {
                throw new Exception("不是四个数");
            }
            for (int i = 0; i < operators.Length; i++)
            {
                string op = operators[i];
                double result1 = GetTwoNumCaculate(array[0], array[1], op);
                if (!IsValidResult(result1))
                {
                    continue;
                }
                String expressionStr1 = $"({array[0]}{op}{array[1]})";
                for (int j = 0; j < operators.Length; j++)
                {
                    string op2 = operators[j];
                    double result2 = GetTwoNumCaculate(array[2], array[3], op2);
                    if (!IsValidResult(result2))
                    {
                        continue;
                    }
                    String expressionStr2 = $"({array[2]}{op2}{array[3]})";
                    for (int k = 0; k < operators.Length; k++)
                    {
                        string op3 = operators[k];

                        double result3 = GetTwoNumCaculate(result1, result2, op3);
                        String expressionStr3 = $"{expressionStr1} {op3} {expressionStr2}";
                        if (result3 == 24.0d)
                        {
                            count++;
                            Console.WriteLine($"方案： {expressionStr3} = {result3}");

                        }
                    }
                }

            }
            return count;
        }

        /// <summary>
        /// 是否为合法的计算结果
        /// </summary>
        /// <param name="result"></param>
        /// <returns></returns>
        public static bool IsValidResult(double result)
        {
            if (result < 1)
            {
                return false;
            }
            return result == Math.Floor(result);
        }


        private static double GetTwoNumCaculate(double num1, double num2, string operatorStr)
        {

            switch (operatorStr)
            {
                case "+":
                    return num1 + num2;
                case "-":
                    return num1 - num2;
                case "*":
                    return num1 * num2;
                case "/":
                    return num1 / num2;
                default:
                    throw new Exception("运算符不符合规范");
            }
        }


    }
}

 

学有所得

1. 是否学会了这种分析思路
2. 是否这种需求分析思路可以运用在地方？
3. 这种把每个原子需求编排成一个完整大需求，是否可以在他地方使用?

最后效果图：