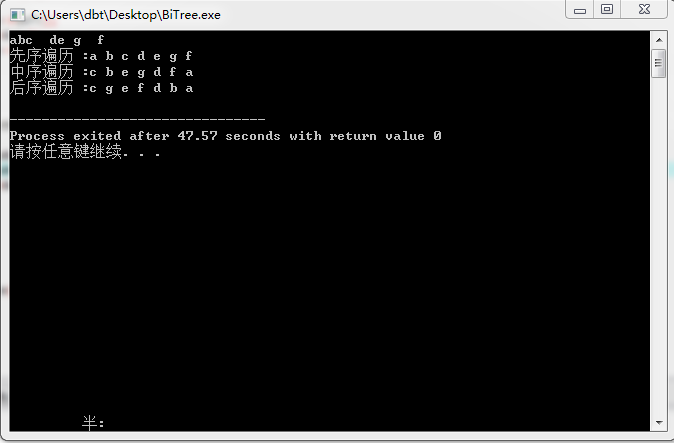
链式二叉树遍历算法实现（递归法）

　　遍历二叉树的常用方法有四种：先（根）序遍历，中（根）序遍历，后（根）序遍历，层序遍历。本文只考虑用递归方法实现先序遍历，中序遍历，后序遍历算法。

• 先序遍历二叉树的操作定义如下：

　　若二叉树为空，则空操作；否则

　　（1）访问根节点；

　　（2）先序遍历左子树；

　　（3）先序遍历右子树。

• 中序遍历二叉树的操作定义如下：

　　若二叉树为空，则空操作；否则

　　（1）中序遍历左子树；

　　（2）访问根节点；

　　（3）中序遍历右子树。

• 后序遍历二叉树的操作定义如下：

　　若二叉树为空，则空操作；否则

　　（1）后序遍历左子树；

　　（2）后序遍历右子树；

　　（3）访问根节点。

 　　上述三种遍历算法实现如下：

 

#include <stdio.h>
#include <stdlib.h>

typedef struct BiTNode {
    int data;
    struct BiTNode *left;
    struct BiTNode *right;
} Node;

//按先序序列建立一个二叉树 
Node* CreateBiTree() {
    char ch;
    
    scanf("%c", &ch);
    if (ch == ' ') {
        return 0;
    } else {
        Node* pstNode = (Node *)malloc(sizeof(Node));
        if (pstNode) {
            pstNode->data = ch;                    //根节点值 
            pstNode->left = CreateBiTree();        //创建左子树 
            pstNode->right= CreateBiTree();     //创建右子树 
        }
    }
}

void DestroyBiTree(Node **ppstNode) {
    if (0 == ppstNode) {
        return;
    }
    if (0 == *ppstNode) {
        return;
    }
    
    if ((*ppstNode)->left) {
        DestroyBiTree(&((*ppstNode)->left));
    }
    if ((*ppstNode)->right) { 
        DestroyBiTree(&((*ppstNode)->right));
    }
    free(*ppstNode);
    *ppstNode = 0;
}

//先序遍历 
void PreOrderTraverse(Node *pstNode) {
    if (pstNode) {
        printf("%c ", pstNode->data);
        PreOrderTraverse(pstNode->left);
        PreOrderTraverse(pstNode->right);
    }
}

//中序遍历 
void InOrderTraverse(Node *pstNode) {
    if (pstNode) {
        InOrderTraverse(pstNode->left);
        printf("%c ", pstNode->data);
        InOrderTraverse(pstNode->right);
    }
}

//后序遍历 
void PostOrderTraverse(Node *pstNode) {
    if (pstNode) {
        PostOrderTraverse(pstNode->left);
        PostOrderTraverse(pstNode->right);
        printf("%c ", pstNode->data);
    }
}

int main () {
    Node *pstNode = CreateBiTree();
    
    printf("先序遍历 :"); 
    PreOrderTraverse(pstNode); 
    printf("\n");
    
    printf("中序遍历 :"); 
    InOrderTraverse(pstNode); 
    printf("\n");
    
    printf("后序遍历 :"); 
    PostOrderTraverse(pstNode); 
    printf("\n");
    
    DestroyBiTree(&pstNode);
    
    return 0;
}

 

　　上述程序在遍历之前先使用函数CreateBiTree()创建了一个二叉树，创建二叉树时使用的是先序序列，使用先序序列生成二叉树的过程和先序遍历的实现类似。测试时，输入先序序列，比如：ABCΦΦDEΦGΦΦFΦΦΦ（Φ代表空格），此先序序列对应的二叉树如下图所示：

 

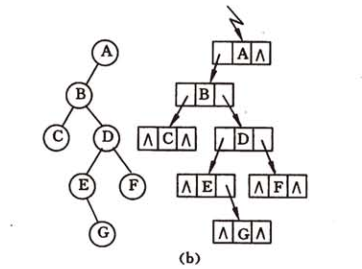
　　对上图所示二叉树的遍历结果（忽略输入大小写）如下图所示：