Deep Learning2: PCA and Whitening
在Technion的暑期学校上,其实已经学过PCA,一直稀里糊涂的,知识点没有串起来
PCA和whitening 是对于数据的预处理,提高运算效率
1. PCA Principal Components Analysis 主成分析法
降低维度,数据可视化 先均值化,再将不同维度数据归一化到同一维(除以最大值)
也就是对数据进行压缩,在降维的同时能够最大程度保留数据特征
将原始数据投射到低维度空间,求正交向量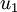
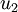 步骤如下,数据在主成分保留的特征最多
步骤如下,数据在主成分保留的特征最多
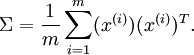
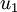
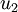 分别是矩阵的第一特征向量和第二特征向量
分别是矩阵的第一特征向量和第二特征向量
得到矩阵U
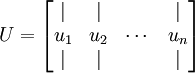
接下来对数据进行转换
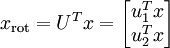
降维操作即只保留主要成分,其他设为0
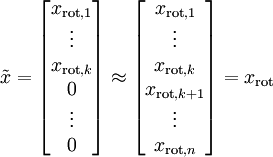
还原数据
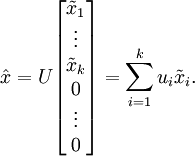
那么设定保留下来的主成分数量k 取决于保留率the percentage of variance retained
the percentage of variance retained is given by:
在图像处理,要求k的最小取值满足
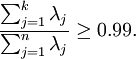
一般,满足1)特征值几乎均值为零2)不同特征值方差近似
对于图像处理,由于其稳定性stationarity,2)方差已经相等,所以只用进行均值归零化
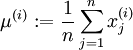
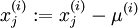
2. Whitening
去除噪声,消除冗余数据,特征之间相关性更小且方差相等
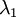 and
and 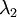 是特征值,就是矩阵的对角值
是特征值,就是矩阵的对角值
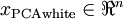 as follows:
as follows:
ZCA Whitening 一般不进行降维操作
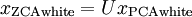
posted on 2016-10-13 17:00 Beginnerpatienceless 阅读(142) 评论(0) 收藏 举报

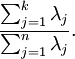
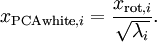

 浙公网安备 33010602011771号
浙公网安备 33010602011771号