机器学习算法（四）：神经网络

基本的神经网络的学习器，通过模拟生物系统对真实世界物体的反应建立如下模型。

 

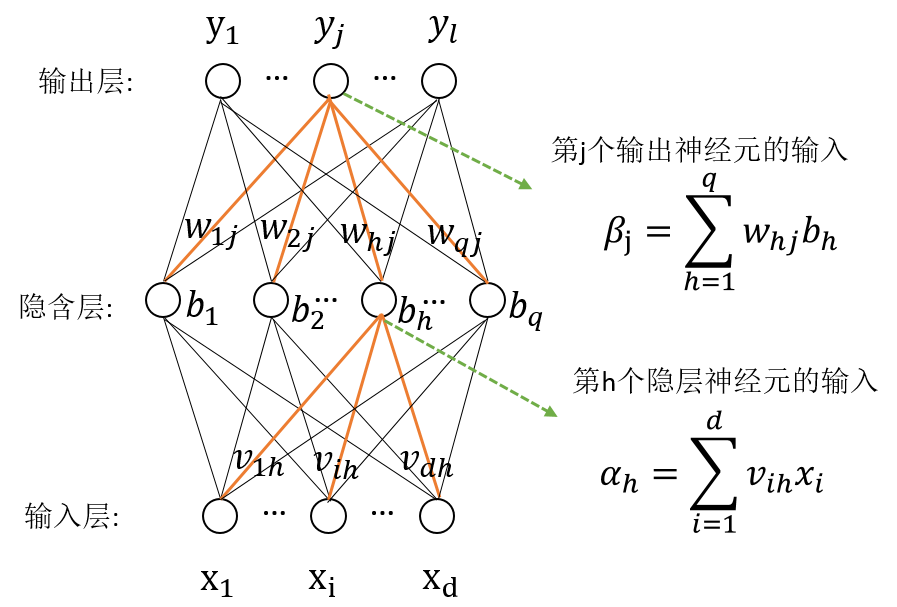
其中，上图的隐含层和输出层的节点是基于感知机模型，如下图将输入值映射到输出值，其中w是连接权重，$\theta$是该节点的阈值，f是激活函数。

常用的激活函数有

1）阶跃函数, 它把输入值映射为0或1

$$ sgn(x)=\left\{
\begin{aligned}
1 & , & x>=0 \\
0 & , & x<0 \\
\end{aligned}
\right.
$$

2）Sigmoid函数，它把输入值映射为(0,1)范围内

$$sigmoid(x) = \frac{1}{1+e^{-x}}$$

感知机模型可以容易实现逻辑与，或，非等线性可分的问题。但要实现非线性可分的问题，则需要在输入和输出之间引入隐含层，理论上只要隐含层的神经元组该多，神经网络模型可以以任意精度毕竟任意复杂度的连续函数。

  

如何求解神经网络的连接权重w和阈值$\theta$

 

这里介绍最常用的误差逆传播(BackPropagation, 简称BP）算法。

首先我们的目标是最小化所有样本的均方误差。为了简化，我们逐个对每一个样本最小化均方误差。下面是第k个样本的均方误差。

$$E_{k} = \frac{1}{2}\sum\limits_{j=1}^{l} (\hat {y}_{j}^{k} - y_{j}^{k})^{2}$$

其中$\hat {y}_{j}^{k} = f(\beta_{j} - \theta_{j})$，基于梯度下降策略，对输出层和隐层之间的w进行调整

$$\Delta w_{hj} = - \eta \frac{\partial E_{k}}{\partial w_{hj}} = - \eta \frac{\partial E_{k}}{\partial \hat {y}_{j}^{k}} \frac{\partial \hat {y}_{j}^{k}}{\partial \beta_{j}} \frac{\partial \beta_{j}}{\partial w_{hj}}$$

利用Sigmoid函数的一个特性$f^{'}(x) = f(x) (1-f(x))$, 可以推导出

$$\Delta w_{hj} = \eta g_{j}b{h}$$ 其中 $$g_{j} = \hat {y}_{j}^{k} (1-\hat {y}_{j}^{k})({y}_{j}^{k} - \hat {y}_{j}^{k}) $$

 类似地可以求出$\Delta \theta_{j}$, $\Delta v_{ih}$, $\Delta \gamma_{h}$，这样通过一个样本把神经网络中的所有参数更新一遍。

可以看到BP算法，就是根据输出层的误差，逆向传播到隐层和输出层，更新连接权重和阈值

 

BP算法在单隐层网络中容易收敛，但是在多隐层神经网络中往往难以收敛。