小橙书阅读指南（十二）——无向图、深度优先搜索和路径查找算法

在计算机应用中，我们把一系列相连接的节点组成的数据结构，叫做图。今天我们将要介绍它的一种形式——无向图，以及针对这种结构的深度优先搜索和路径查找算法。

一、无向图数据结构

接口：

/**
 * 图论接口
 */
public interface Graph {
    /**
     * 顶点数
     *
     * @return
     */
    int vertexNum();

    /**
     * 边数
     *
     * @return
     */
    int edgeNum();

    /**
     * 向图中添加一条v-w的边
     *
     * @param v
     * @param w
     */
    void addEdge(int v, int w);

    /**
     * 和v相邻的所有顶点
     *
     * @param v
     * @return
     */
    Iterable<Integer> adjoin(int v);

    /**
     * v的维度
     *
     * @param v
     * @return
     */
    int degree(int v);
}

实现类：

public class Graph implements algorithms.graphs.ifs.Graph {
    private final int vertex; // 顶点
    private int edge; // 边
    private ArrayList<Integer>[] adj;

    public Graph(int v) {
        this.vertex = v;
        this.edge = 0;
        adj = (ArrayList<Integer>[]) new ArrayList[v];
        for (int i = 0; i < v; i++) {
            adj[i] = new ArrayList<>();
        }
    }

    @Override
    public int vertexNum() {
        return vertex;
    }

    @Override
    public int edgeNum() {
        return edge;
    }

    @Override
    public void addEdge(int v, int w) {
        validateVertex(v);
        validateVertex(w);
        adj[v].add(w);
        adj[w].add(v);
        edge++;
    }

    @Override
    public Iterable<Integer> adjoin(int v) {
        return adj[v];
    }

    @Override
    public int degree(int v) {
        return adj[v].size();
    }

    private void validateVertex(int v) {
        if (v < 0 || v > this.vertex) {
            throw new IllegalArgumentException();
        }
    }
}

二、深度搜索优先算法

对于图的处理我们常常通过系统地检查每一个顶点和每一条边来获取图的各种性质。对于图的问题我们最经常被问及的是：a点和b点连通吗？如果连通如何到达？为了描述方便，我们使用自然数描述图的每一个顶点。

假设有以下图的结构

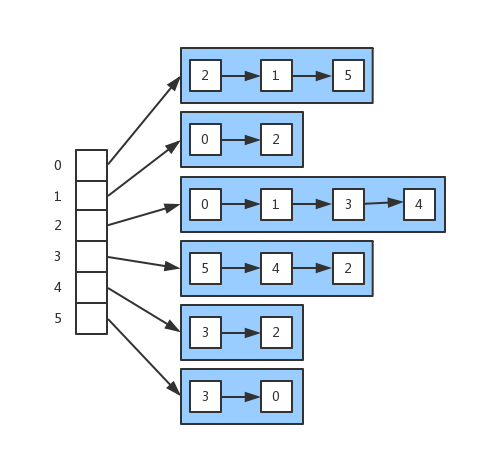
 左侧数组表示节点，右侧代表与节点连接的其他节点。该结构的标准画法如下：

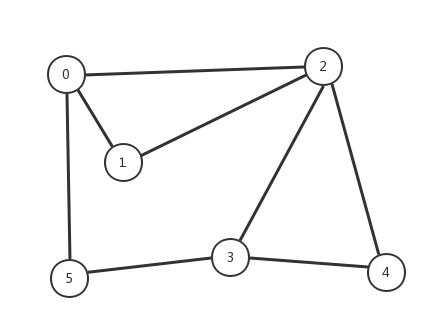
算法描述：深度优先搜索从起点出发（0）遍历（2，1，5）并递归（2）与它链接的点，被搜索到的点将不会被再次递归直到所有的点都被搜索到为止。

深度优先搜索接口与实现：

// 接口
public interface Search {
    boolean marked(int v);
    int count();
}

/**
 * 图论：深度优先搜索
 */
public class DepthFirstSearch implements Search {
    private boolean[] marked;
    private int count;

    public DepthFirstSearch(Graph g, int s) {
        marked = new boolean[g.vertexNum()];
        validateVertex(s);
        dfs(g, s);
    }

    /**
     * 以递归的方式从s起点出发，标记每一个经过的顶点，未被标记的顶点为不连通
     *
     * @param g
     * @param v
     */
    private void dfs(Graph g, int v) {
        marked[v] = true;
        count++;
        for (int x : g.adjoin(v)) {
            if (!marked[x]) {
                dfs(g, x);
            }
        }
    }

    @Override
    public boolean marked(int v) {
        validateVertex(v);
        return marked[v];
    }

    @Override
    public int count() {
        return count;
    }

    // throw an IllegalArgumentException unless {@code 0 <= vertexNum < V}
    private void validateVertex(int v) {
        int V = marked.length;
        if (v < 0 || v >= V)
            throw new IllegalArgumentException();
    }

}

这套算法的核心是dfs函数。我们要理解深度优先算法就必须弄清楚算法递归的过程。marked数组记录节点的访问情况，变量x和v的递归过程如下：

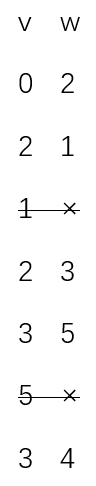
标准画法：

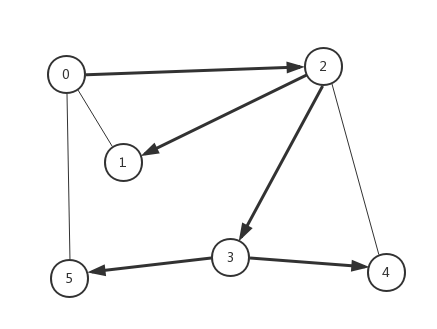
 深度优先算法按照上面的路径搜索图，由此我们可以获知深度搜索算法的两个特征：

1.搜索路径沿一条路径向下扩展，每一个节点只会被遍历一次（每一个节点都可以知道在搜索路径上的上一个节点，并唯一确定）。

2.搜索路径上的任意两点代表可达，但并非最短路径。

这样我们就可以回答本文最早提出的有关图的第一个问题：a点和b点连通吗？显然，以a为起点搜索整个图，如果b点在路径上则表示连通。

三、使用深度优先搜索的路径算法

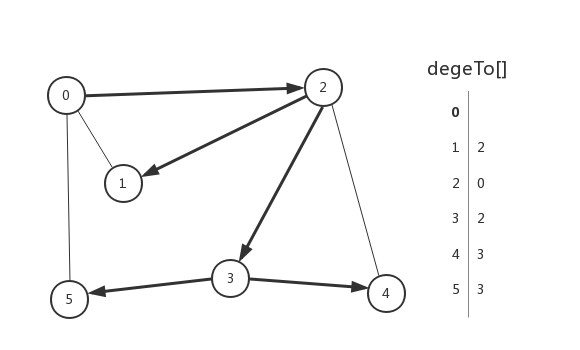
要回答有关图的第二个问题：如果连通如何到达？回忆上一段我们总结的深度搜索算法的第一个特征，我们可以使用数组结构在存储每一个节点的上一个节点。

路径搜索接口和实现：

/**
 * 寻找路径
 */
public interface Paths {
    boolean hasPathTo(int vertex);

    Iterable<Integer> pathTo(int vertex);
}

/**
 * 基于深度优先搜索的路径搜索算法
 */
public class DepthFirstPaths implements Paths {
    private final int s;
    private boolean[] marked;
    private int[] edgeTo;

    public DepthFirstPaths(Graph g, int s) {
        this.s = s;
        marked = new boolean[g.vertexNum()];
        edgeTo = new int[g.vertexNum()];
        dfs(g, s);
    }

    private void dfs(Graph g, int v) {
        marked[v] = true;
        for (int w : g.adjoin(v)) {
            if (!marked[w]) {
                edgeTo[w] = v;
                dfs(g, w);
            }
        }
    }

    @Override
    public boolean hasPathTo(int vertex) {
        return marked[vertex];
    }

    @Override
    public Iterable<Integer> pathTo(int vertex) {
        if (!hasPathTo(vertex)) {
            return null;
        }
        Stack<Integer> path = new Stack<>();
        for (int i = vertex; i != s; i = edgeTo[i]) {
            path.push(i);
        }
        path.push(s);
        return path;
    }
}

 算法的标准画法：

相关链接：

Algorithms for Java