图形辅助，理解递归

对大多数程序员来说，递归算法都不算陌生。甚至很多时候，使用递归算法解决一些简单问题是基础教材的起步课程。但是，当递归算法遇到稍微复杂的数据结构，如二叉搜索树的时候。别说让你直接写出算法，就是把标准答案摆在你的面前让你理解，我们恐怕都会抓耳挠腮。如果你也有类似的困扰请不要灰心，因为包括我在内几乎我遇到的每一个码农在这些方面都显得一筹莫展。究其原因，我认为这其实是认知心理的一种表现——我们无法胜任同时正向思考与反向记忆——大多数的时候，我们可以轻松应付函数的一层层递进，却很难记住每一层的返回值。终于我发现通过一种简单而有效的图形结构可以让我们理解各类递归算法，下面进入正题。

定义在一个标准的二叉搜索树算法中包含一个方法以获取小于某一个键值Key的最大节点对象：

/**
 * Node包含一个键值对<Key extends Comparable<Key>, Value>
 * 以及一棵左子树和一棵右子树Node left, right
 *
 * class Node {
 *     private Key key;
 *    private Value val;
 *    private Node left, right;
 * }
 */
Node floor(Node n, Key key) {
    if (n == null) {
        return null;
    }
    int cmp = key.compareTo(n.key);
    if (cmp == 0) {
        return n;
    } else if (cmp < 0) {
        return floor(n.left, key);
    } else {
        Node r = floor(n.right, key);
        if (r != null) {
            return r;
        } else {
            return n;
        }
    }
}

算法不复杂，对二叉搜索树不太了解的可以先去熟悉一下数据结构。可是想读懂这几行代码确实令我头疼，毕竟如果读不懂就不可能记住更不可能在需要的时候自己写出来。接下来就是见证奇迹的时刻：

首先，任何一种递归算法都必然包含四种要素：输入，输出，递归条件和终止条件。floor方法含有两个递归条件cmp<0和cmp>0以及三个终止条件n==null, cmp==0和r==null。

其次，我们将要通过简单的图形来代表层层的递归顺序，并且帮助我们在达到终止条件的时候记录返回值。如果在稿纸上绘制甚至还可以更简洁一些。

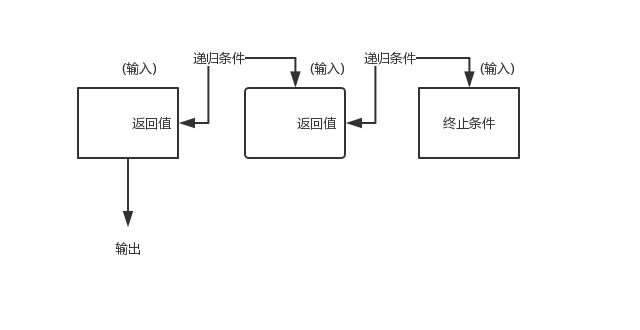
以下是一个完整的演示: Node(H) floor( Node(S), Key(J) )

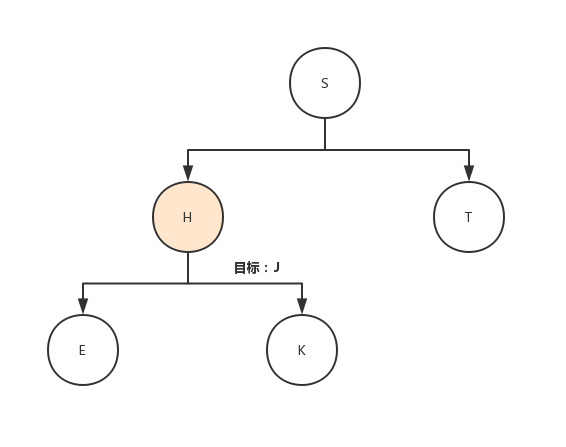
跟着floor方法绘制递归图你大概应该获得和我类似的结果：

是不是感觉瞬间思路清晰了！如果你也觉得这样的方法对你有所帮助或者还有更好的建议不妨在留言中分享出来。