用线性规划建模（确定参数）关键路径法
用线性规划建模（确定参数）关键路径法
关键路径法(CPM)又称为网络计划法，是项目管理的基本方法。项目管理关心项目的执行时间和执行费用等问题，首先的是项目的总工期，其次是组成项目的工作的开始完成时间和结束完成时间及其对总工期的影响，而后是当项目需要压缩工期时，每个项目任务的工期是否需要压缩、压缩量是多少等问题。在整个项目中，有一系列首尾相接的任务，他们的浮动时差为0，组成了所谓关键路径。如果某个关键路径上的任务一旦延期，则总工期一定会延期，除非压缩其他关键路径上的任务的工期。这里先讨论确定参数时的关键路径法。
最小总工期和关键路径寻找的线性规划模型
以[1]中第八章的一个例题为例，假设有A,B,C,D,E,F五项任务组成了项目，他们执行时长和紧前任务如下表所示：
按照上面的信息可以画出网络计划图：
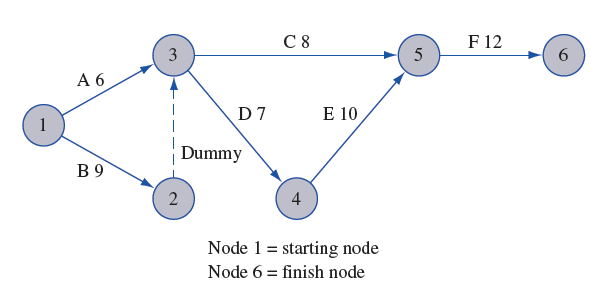
这个图里的A任务用弧(1,3)表示，其执行时长度为6。C认为用弧(3,5)表示，执行时间长度为8。C任务的紧前任务是A和B。Dummy任务是执行时长为0的虚任务，作用是避免同样的弧（即点对）表示不同的任务。例如不采用Dummy时，任务A和任务B都会用弧(1,3)表示而产生歧义。
对于上面的网络计划图，建立线性规划模型时必须给予表达。方法是出所有弧及弧上的权（即执行时长）：
G={ 1 2 9 1 3 6 2 3 0 3 4 7 3 5 8 4 5 10 5 6 12 }
用变量x[i]表示第i节点的执行时刻，于是线性规划的目标即极小化总工期，即min x[N]-x[1]。这里 N=6，是项目的结束节点编号，也是节点的数目。
min x[N]-x[1]
线性规划的约束只要保证任务的执行时间长度就可以了：
x[G[k][2]] - x[G[k][1]] >= G[k][3] | k=1,..., NE
上面假设G里面共有NE条边，则对任意一条边k (k=1,...,NE), 其弧上第二节点的执行时刻x[G[k][2]]与第一节点的执行时刻x[G[k][1]]之差应大于等于该项任务的执行时长G[k][3]。
有必要把x[1]设为0：
x[1]=0
把目标和约束写在一起：
min x[N]-x[1] subject to x[G[k][2]] - x[G[k][1]] >= G[k][3] | k=1,...,NE x[1]=0
上面的模型还不能够被求解，缺少符号的说明和数据，加上后这样：
min x[N]-x[1] subject to x[G[k][2]] - x[G[k][1]] >= G[k][3] | k=1,...,NE x[1]=0 where N,NE are numbers G[k][j] is a number | k=1,...,NE; j=1,...,3 x[i] is a variable of nonnegative number|i=1,...,N data N=6 NE=7 G={ 1 2 9 1 3 6 2 3 0 3 4 7 3 5 8 4 5 10 5 6 12 }
在+Leapms软件中对上面的模型进行求解得到：
+Leapms>solve The LP is solved to optimal. 找到线性规划最优解.非零变量值和最优目标值如下： ......... x2*=9 x3*=9 x4*=16 x5*=26 x6*=38 ......... Objective*=38 .........
得知项目的最短工期为38。如果想获取关键路径信息需要利用对偶值。首先使用savelp命令获得lp模型（即展开的代数模型）。
\==================================\ \Problem cpm \.lp file gnerated by +Leapms \==================================\ Minimize Obj: -x1+x6 Subject to C1: -x1+x2>=9 C2: -x1+x3>=6 C3: -x2+x3>=0 C4: -x3+x4>=7 C5: -x3+x5>=8 C6: -x4+x5>=10 C7: -x5+x6>=12 C8: x1=0 End \==================================\
而后使用dual命令获取当前的对偶解：
+Leapms>dual dual[1]*=1 dual[2]*=0 dual[3]*=1 dual[4]*=1 dual[5]*=0 dual[6]*=1 dual[7]*=1 dual[8]*=0
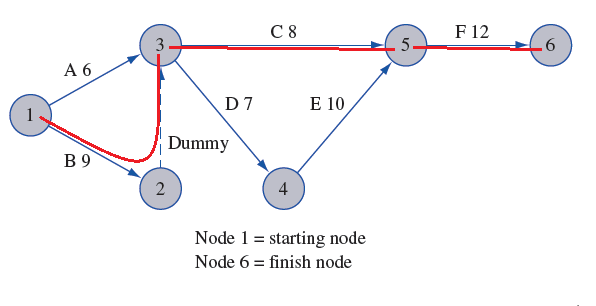
忽略对偶为0的对偶变量，得关键路径为边（即lp模型里的约束）C1,C3,C4,C6,C7, 对应于弧(1,2), (2,3), (3,5), (5,6). 即关键路径如下：
参考文献
[1] WayneL.Winston, 韦恩·L.温斯顿, 温斯顿. Operations research[M]// OPERATIONS RESEARCH. 2011.
