旅游公司租车问题 —— 动态规划 v.s. + Leapms线性规划
有一个旅游公司承包一条旅游线路,未来四周内的大巴车需求分别是:4辆、1辆、4辆和5辆。该公司向租车公司租赁服务,租车公司的计价方案是:租车收取一次性手续费3000,每车每周费用2000。求最节省租车方案。
线性规划方法
参数定义:
d[k]: 第k周的需求车数;
s[k]: 第k周周初库存车辆数量;
x[k]: 第k周周初租车数量;
y[k]第k周周初还车数量。
目标
数学式:
$\min \sum_{k=1}^{n}(3000x_k+2000(x_k+s_k-y_k))$
+Leapms形式:
min sum{k=1,...,n}(3000x[k]+2000(x[k]+s[k]-y[k]))
约束(+Leapms形式):
s[k]+x[k]-y[k] ≥ d[k] | k=1,...,n // 每周车辆需求约束
s[k+1] =s[k] + x[k] - y[k] | k=1,...,n-1 //库存变化逻辑
数据:
n=4
d={4 1 4 5}
完整+Leapms模型:
min sum{k=1,...,n}(5000x[k]+2000(s[k]-y[k])) subject to x[k]+s[k]-y[k]>=d[k]| k=1,...,n s[k+1]=x[k]+s[k]-y[k]| k=1,...,n-1 s[1]=0 where n is a number d is a set x[k],s[k],y[k] are variables of nonnegative numbers --> |k=1,...,n data n=4 d={4 1 4 5}
直接求解
在 +Leapms 中使用 load 和 mip 命令求解。
Welcome to +Leapms ver 1.1(162260) Teaching Version -- an LP/LMIP modeling and
solving tool.欢迎使用利珀 版本1.1(162260) Teaching Version -- LP/LMIP 建模和求
解工具.
+Leapms>load
Current directory is "ROOT".
.........
tour_bus.leap
.........
please input the filename:tour_bus.leap
================================================================
1: min sum{k=1,...,n}(5000x[k]+2000(s[k]-y[k]))
2: subject to
3: x[k]+s[k]-y[k]>=d[k]| k=1,...,n
4: s[k+1]=x[k]+s[k]-y[k]| k=1,...,n-1
5: s[1]=0
6: where
7: n is a number
8: d is a set
9: x[k],s[k],y[k] are variables of nonnegative numbers -->
10: |k=1,...,n
11: data
12: n=4
13: d={4 1 4 5}
================================================================
>>end of the file.
Parsing model:
1D
2R
3V
4O
5C
6S
7End.
..................................
number of variables=12
number of constraints=8
..................................
+Leapms>mip
relexed_solution=49000; number_of_nodes_branched=0; memindex=(2,2)
The Problem is solved to optimal as an MIP.
找到整数规划的最优解.非零变量值和最优目标值如下:
.........
s2* =4
s3* =4
s4* =4
x1* =4
x4* =1
.........
Objective*=49000
.........
+Leapms>
得到最优解: x1*=4, x4*=1, x2*=x3*=0, 目标函数值:49000。
CPLEX求解
在+Leapms环境中输入cplex命令,即可触发CPLEX求解器对问题进行求解。
+Leapms>cplex You must have licience for Ilo Cplex, otherwise you will violate corresponding copyrights, continue(Y/N)? 你必须有Ilo Cplex软件的授权才能使用此功能,否则会侵犯相应版权, 是否继续(Y/N)?y +Leapms>
Tried aggregator 1 time.
LP Presolve eliminated 2 rows and 3 columns.
Aggregator did 1 substitutions.
Reduced LP has 5 rows, 8 columns, and 15 nonzeros.
Presolve time = 0.02 sec. (0.01 ticks)
Iteration log . . .
Iteration: 1 Dual infeasibility = 4000.000000
Iteration: 4 Dual objective = 46000.000000
Solution status = Optimal
Solution value = 49000
s2=4
s3=4
s4=4
x1=4
x4=1
+Leapms - Latex数学概念模型
在+Leapms环境下,使用 “latex"命令可以把上面的+Leapms模型直接转换为如下Latex格式的数学概念模型

动态规划方法:
dk: 第k周的需求车数;sk : 第k周周初库存车辆数量;xk: 第k周周初租车数量;yk第k周周初还车数量。
递推方程:
f(sk)=min{3000xk+2000(sk-yk)+f(sk+1)), (1)
其中 sk+1=sk+xk-yk, (2)
sk+1≥dk, (3)
xk≥0, yk≥0。 (4)
<代数式求解非常繁琐> 。。。
图解法:
(1)根据题意,共四个阶段, 把状态取为阶段最后时刻的保有车数,每个周期的最大状态是5,最小是该阶段用车数量。画出阶段及状态:

(2)画出状态转移和决策含义:
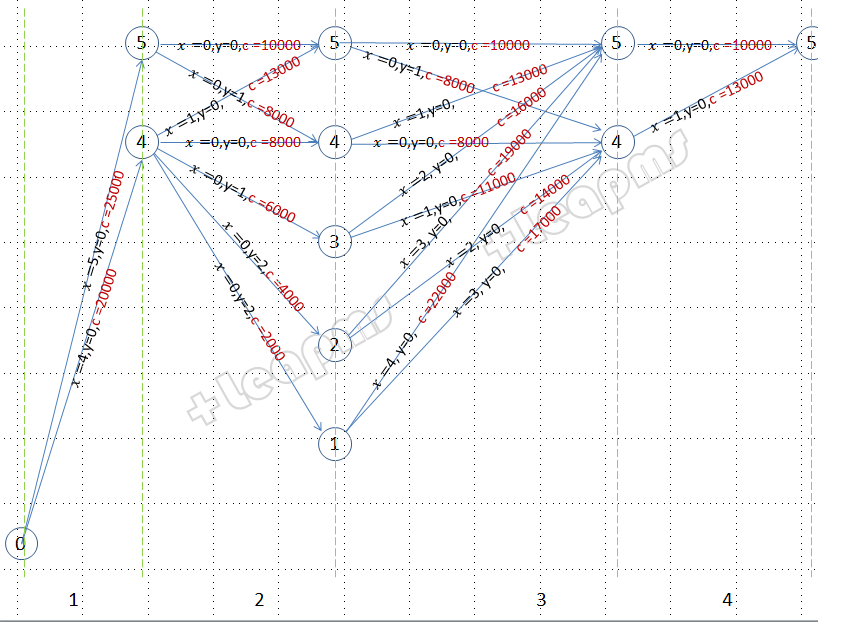
(3)使用倒序法递推最优解:
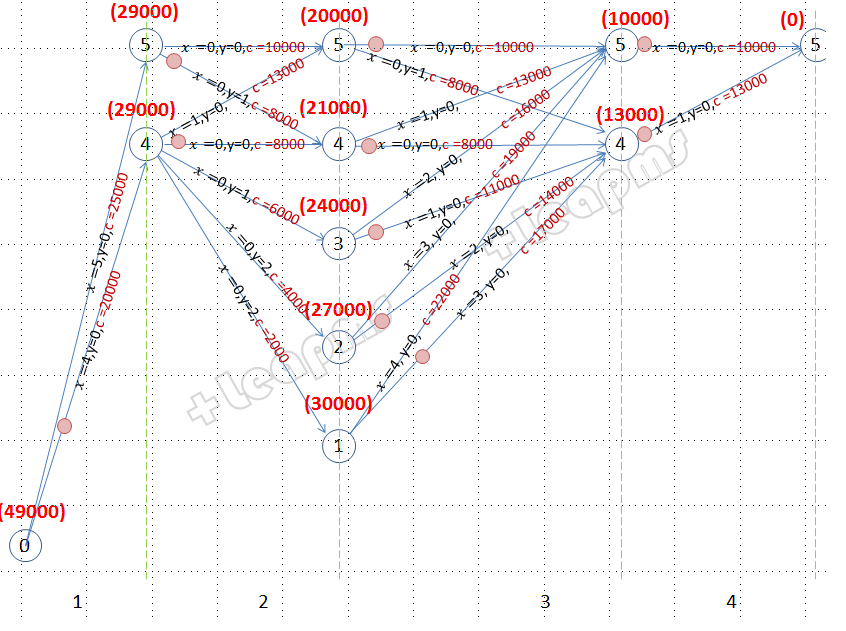
(4) 得到最优解: x1*=4, x4*=1, x2*=x3*=0, 目标函数值:49000:




 浙公网安备 33010602011771号
浙公网安备 33010602011771号