从一段简单算法题来谈二叉查找树(BST)的基础算法
先给出一道很简单,喜闻乐见的二叉树算法题:
给出一个二叉查找树和一个目标值,如果其中有两个元素的和等于目标值则返回真,否则返回假。
例如:
Input: 5 / \ 3 6 / \ \ 2 4 7 Target = 9 Output: TrueInput: 5 / \ 3 6 / \ \ 2 4 7 Target = 28 Output: False
什么是二叉树?
二叉树是每个节点最多有两个子树的树结构。
什么是二叉查找树(binary search tree)
二叉排序树或者是一棵空树,或者是具有下列性质的二叉树:
(1)若左子树不空,则左子树上所有结点的值均小于或等于它的根结点的值;
(2)若右子树不空,则右子树上所有结点的值均大于或等于它的根结点的值;
(3)左、右子树也分别为二叉排序树;
二叉树的遍历
1.先序遍历(pre-order)
首先访问根结点然后遍历左子树,最后遍历右子树。在遍历左、右子树时,仍然先访问根结点,然后遍历左子树,最后遍历右子树,如果二叉树为空则返回。
2.后序遍历( post-order )
后序遍历首先遍历左子树,然后遍历右子树,最后访问根结点,在遍历左、右子树时,仍然先遍历左子树,然后遍历右子树,最后遍历根结点。
3.中序遍历(in-order)
中序遍历首先遍历左子树,然后访问根节点,然后遍历右子树。
举个例子:
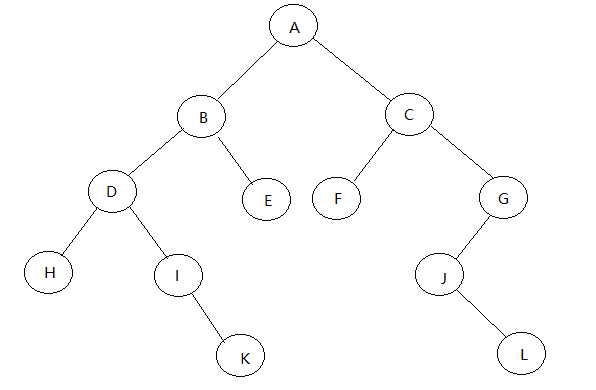
先序遍历节点遍历顺序: A B D H I K E C F G J L
后序遍历节点遍历顺序: H K I D E B F L J G C A
中序遍历节点遍历顺序: H D I K B E A F C J L G
算法题解法
1.使用HashSet
最简单的解法就是遍历整个树,然后得到所有的节点对来判断他们是否能相加得到目标值k。但是我们稍微考虑一下缓存,这个方案还能提高一些。
如果两个元素的和等于k,即x+y=k,并且我们已经知道x是已经存在于树的,我们只要检索y是否也在树的节点里即可,即y=k-x。基于这个简单的缓存,我们可以在每一步去遍历这棵树的两个方向(左子树和右子树)。我们使用一个集合来存遍历过程中被遍历过的元素。
对于每一个当前的节点,有值p,我们去检查k-p是否存在于集合中。如果存在的话,我们可以得到存在2个元素的值等于k的结论。否则,我们继续把这个值存进集合。
如果遍历了整棵树后,没有这样的p值,那就证明不存在2个元素的值相加等于k。
代码如下:
public class Solution { public boolean findTarget(TreeNode root, int k) { Set<Integer> set = new HashSet(); return find(root, k, set); } public boolean find(TreeNode root, int k, Set < Integer > set) { if (root == null) return false; if (set.contains(k - root.val)) return true; set.add(root.val); return find(root.left, k, set) || find(root.right, k, set); } }
//时间复杂度为 O(n),空间复杂度也为O(n).
2.使用BFS和HashSet.
在这个解法中,使用HashSet的想法和解法1是一样的。但是我们在遍历的时候使用广度优先算法(Breadth First Search),这是一个在树的遍历算法中很常用的算法。BFS的方法如如下总结的一样。我们在开始的时候把根节点放进一个队列。
我们还是会用到如上解法的一个集合。然后在每一步我们会这么做:
1.从队列queue的头部去除一个元素p。
2.判断k-p是否存在于集合中。如果是,返回true。
3.否则,把这个元素p加到集合中。然后,把这个节点的左右子节点加到队列queue的末尾。
4.继续1-3步骤,直到队列为空。
5.如果队列为空,则返回false。
照这个步骤,我们一层一层的循环了整个树。
代码如下:
public class Solution { public boolean findTarget(TreeNode root, int k) { Set<Integer> set = new HashSet(); Queue<TreeNode> queue = new LinkedList(); queue.add(root); while (!queue.isEmpty()) { if (queue.peek() != null) { TreeNode node = queue.remove(); if (set.contains(k - node.val)) return true; set.add(node.val); queue.add(node.right); queue.add(node.left); } else queue.remove(); } return false; } } //时间复杂度为 O(n),空间复杂度也为O(n).
3.使用BST
在这个解法中,我们要充分利用这个树是一个二叉搜索树。现在,我们知道一个树的中序遍历会得到一个递增的节点集。如此一来,我们可以对这棵树进行中序排序,然后把结果存进一个数组,这个数组的元素按照升序的顺序排列。
上面的步骤做好以后,我们使用l和r两个指针指向数组的开头和结尾。然后,我们这么做:
1.判断l和r指向的节点的值的和是否等于k。如果是,立马返回true。
2.如果他们的和小于k,l移向下一个元素。我们需要得到更大的和,那我们只有提高我们更小的那个值。
3.如果他们的和大于k,r移向上一个元素。我们需要得到更小的和,那我们只有减少我们更大的那个值。
4.循环执行1-3步,直到l和r指针相遇。
5.如果l和r指针相遇,则返回false.
public class Solution { public boolean findTarget(TreeNode root, int k) { List<Integer> list = new ArrayList(); inorder(root, list); int l = 0, r = list.size() - 1; while (l < r) { int sum = list.get(l) + list.get(r); if (sum == k) return true; if (sum < k) l++; else r--; } return false; } public void inorder(TreeNode root, List < Integer > list) { if (root == null) return; inorder(root.left, list); list.add(root.val); inorder(root.right, list); } }
//时间复杂度为 O(n),空间复杂度也为O(n).
至于广度优先算法和深度优先算法,以后有机会再展开吧。


