Treap——浅谈树堆
什么是 Treap
首先,看 Treap 这个单词。
——没错,Tree + heap = Treap。所以,可以看出,Treap就是同时具有(二分查找)树和(大/小根)堆性质的数据结构。
如果你已经对上面二分查找树有所了解,就会发现一个问题——二分查找树在平衡(即左右子树差不多大)时效率十分优秀,但是当它退化成链(比如插入一段单调序列),效率就会变得很低。
所以就诞生了一种数据结构——平衡树,就是为了尽可能在保留二分查找树的性质下又尽可能保持平衡。
为了做到这一点,出现了各种各样奇(du)怪(liu)的平衡树写法(像什么Splay,红黑树,替罪羊树之类算法我是不会的),Treap 就是其中一种。
(无旋 Treap 先鸽着,将来会了有空补)
Treap 保持平衡的原理
我们可以把这个问题分成两部分,一部分是维护元素信息(和输入数据有关),另一部分只是单纯保持树的形态(与输入数据无关)。
所以想让它平衡,很容易想到只需要另一个在随机数据(因为“和输入数据无关”)下可以平衡的数据结构来维护树的形态。
而另一个比较基本的数据结构堆在大量随机数据下基本平衡且使复杂度不退化。所以,可以考虑能否利用堆的思想对其进行优化。
解决方法就是就很暴力地把两个元素加一加——查询、插入之类操作时按二分查找树操作,操作完以后按堆来构造树的形态。
具体的,给每个节点,额外多维护一个“无用”信息 $dat$,让这棵树以这个值按堆构造形态。
但维护形态的关键点是不能影响查询和插入等操作,而这两点与树的中序排列直接相关。
做到这一点,就涉及到了 Treap 最关键的操作——旋转。
(当然还有无旋 Treap,但我还不会a)
旋转
(偷图)
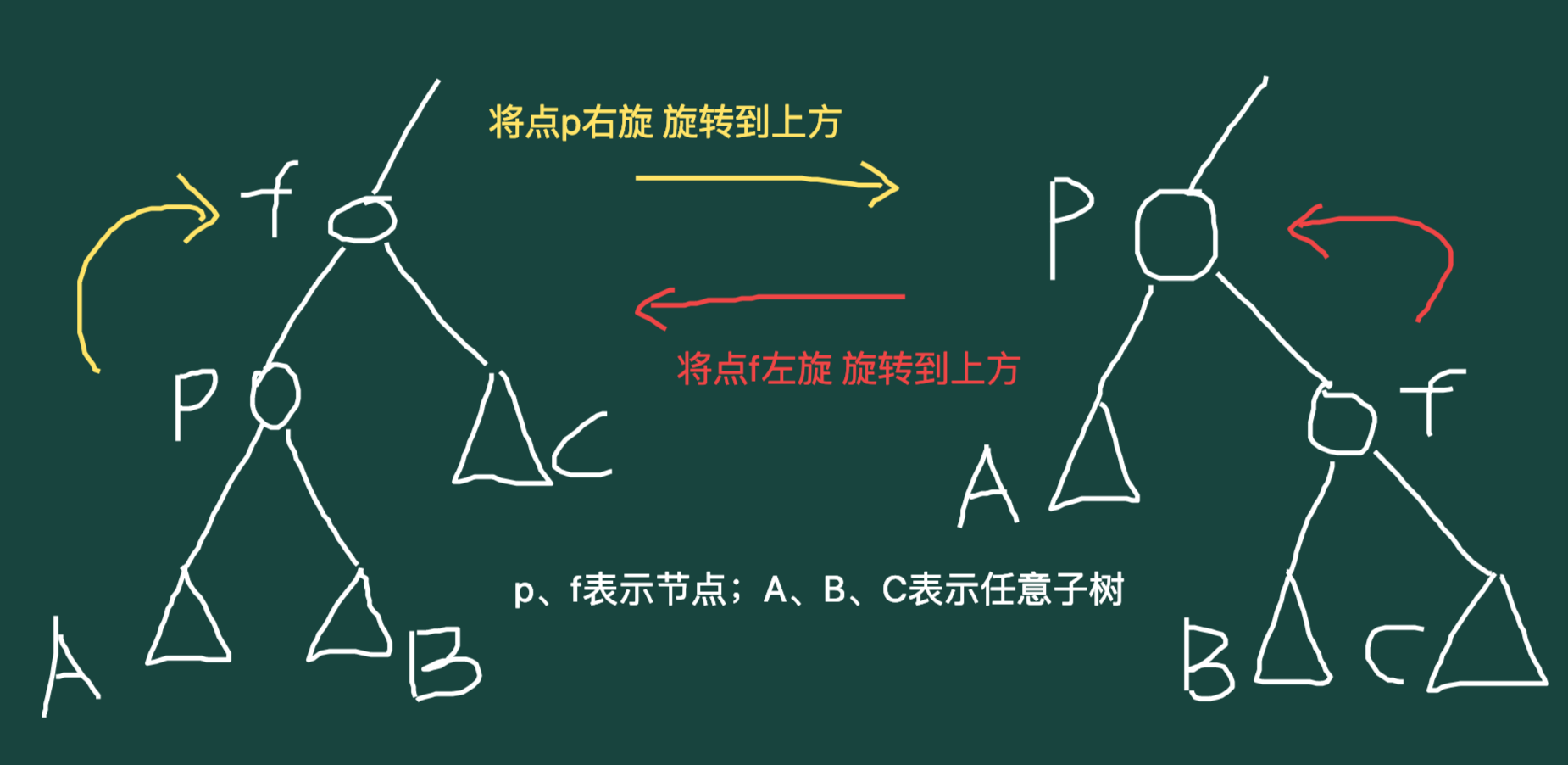
Treap 入门最迷惑的就是旋转操作,分为左旋和右旋,作用是中序排序不变(保持 BST 性质)下防止左儿子或右儿子过重,具体可以看图。
具体实现:以右旋 zig 操作为例,我的理解是把父亲拽下来,作为他原本的左儿子的第三个儿子,然后让原来的左儿子代替他的位置,这样原来的左儿子就有三个儿子了,刚好把第二个儿子作为它原来的父亲(现在的第三个儿子)的左儿子。
左旋 zag 操作类似。
具体实现可以看下面的例题及分段注释——
例题
洛谷传送门,同时这题也可以过这道题的加强版~
【模板】普通平衡树
题目描述
您需要写一种数据结构(可参考题目标题),来维护一些数,其中需要提供以下操作:
-
插入 $x$ 数
-
删除 $x$ 数(若有多个相同的数,因只删除一个)
-
查询 $x$ 数的排名(排名定义为比当前数小的数的个数 $+1$ )
-
查询排名为 $x$ 的数
-
求 $x$ 的前驱(前驱定义为小于 $x$,且最大的数)
-
求 $x$ 的后继(后继定义为大于 $x$,且最小的数)
输入格式
第一行为 $n$,表示操作的个数,下面 $n$ 行每行有两个数 $\text{opt}$ 和 $x$,$\text{opt}$ 表示操作的序号( $ 1 \leq \text{opt} \leq 6 $ )
输出格式
对于操作 $3,4,5,6$ 每行输出一个数,表示对应答案
样例 #1
样例输入 #1
10
1 106465
4 1
1 317721
1 460929
1 644985
1 84185
1 89851
6 81968
1 492737
5 493598
样例输出 #1
106465
84185
492737
提示
【数据范围】
对于 $100%$ 的数据,$1\le n \le 10^5$,$|x| \le 10^7$
代码解析
下面代码是洛谷模板题代码。
(函数的作用和它们的名字一致)
节点内容
struct Treap{ int l,r,dat,val,siz,cnt; }a[N];
分别代表左儿子、右儿子、节点的随机值(用于堆)、节点数值、树大小(包括自身)、该节点保存的数值的数量。
New
int New(int val)
{
a[++tot].val=val;
a[tot].dat=rand(); //随机值,用它保证堆的复杂度
a[tot].cnt=a[tot].siz=1;
return tot;
}
根据值新建一个节点。
Update
void Update(int p)
{
a[p].siz=a[a[p].l].siz+a[a[p].r].siz+a[p].cnt;
}
Build
void Build()
{
New(-inf),New(inf);
root=1,a[1].r=2; //根是1,2号节点是根的右儿子
Update(root);
}
先插入 $inf$ 和 $-inf$,防止查到奇奇怪怪的东西。
GetRankByVal
int GetRankByVal(int p,int val)
{
if(!p) return 1; //空节点返回1,因为这时val是一个不在树中的值
if(val==a[p].val) return a[a[p].l].siz+1;
if(val<a[p].val) return GetRankByVal(a[p].l,val);
return GetRankByVal(a[p].r,val)+a[a[p].l].siz+a[p].cnt;
}
GetValByRank
int GetValByRank(int p,int rank)
{
if(!p) return inf;
if(a[a[p].l].siz>=rank) return GetValByRank(a[p].l,rank); //val比节点值小
if(a[a[p].l].siz+a[p].cnt>=rank) return a[p].val; //找到了
return GetValByRank(a[p].r,rank-a[a[p].l].siz-a[p].cnt);
}
旋转
这个是重点操作,请配合上图食用。
void zig(int& p)
{
int q=a[p].l;
a[p].l=a[q].r,a[q].r=p,p=q;
Update(a[p].r),Update(p);
}
void zag(int& p)
{
int q=a[p].r;
a[p].r=a[q].l,a[q].l=p,p=q;
Update(a[p].l),Update(p);
}
Insert
void Insert(int& p,int val)
{
if(!p){ p=New(val); return; }
if(val==a[p].val){ a[p].cnt++,Update(p); return; } //val就是当前节点值
if(val<a[p].val) //比节点值小,在左儿子
{
Insert(a[p].l,val);
if(a[p].dat<a[a[p].l].dat) zig(p);
}
else //在右儿子
{
Insert(a[p].r,val);
if(a[p].dat<a[a[p].r].dat) zag(p);
}
Update(p);
}
求前驱后驱
前驱后驱代码只改了几个大小于符号,所以这里只放了前驱代码。
int GetPre(int val)
{
int ans=1; //先设为最大值
int p=root;
while(p)
{
if(val==a[p].val) //当前节点等于val
{
if(a[p].l>0) //存在左儿子
{
//因为左儿子子树中的值都比节点大,所以只需要找到左子树最大值,即左子树一直往右走
p=a[p].l;
while(a[p].r>0) p=a[p].r;
ans=p;
}
break;
}
if(a[p].val<val && a[p].val>a[ans].val) ans=p; //找到更优的答案
p=val<a[p].val?a[p].l:a[p].r;
}
return a[ans].val;
}
完整代码
$\color{#83C44D}{\Large\texttt{Show Code}}$
#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<ctime>
using namespace std;
const int N=1e5+5,inf=0x7fffffff;
int n,tot,root;
struct Treap{ int l,r,dat,val,siz,cnt; }a[N];
int New(int val)
{
a[++tot].val=val;
a[tot].dat=rand();
a[tot].cnt=a[tot].siz=1;
return tot;
}
void Update(int p)
{
a[p].siz=a[a[p].l].siz+a[a[p].r].siz+a[p].cnt;
}
void Build()
{
New(-inf),New(inf);
root=1,a[1].r=2;
Update(root);
}
int GetRankByVal(int p,int val)
{
if(!p) return 1;
if(val==a[p].val) return a[a[p].l].siz+1;
if(val<a[p].val) return GetRankByVal(a[p].l,val);
return GetRankByVal(a[p].r,val)+a[a[p].l].siz+a[p].cnt;
}
int GetValByRank(int p,int rank)
{
if(!p) return inf;
if(a[a[p].l].siz>=rank) return GetValByRank(a[p].l,rank);
if(a[a[p].l].siz+a[p].cnt>=rank) return a[p].val;
return GetValByRank(a[p].r,rank-a[a[p].l].siz-a[p].cnt);
}
void zig(int& p)
{
int q=a[p].l;
a[p].l=a[q].r,a[q].r=p,p=q;
Update(a[p].r),Update(p);
}
void zag(int& p)
{
int q=a[p].r;
a[p].r=a[q].l,a[q].l=p,p=q;
Update(a[p].l),Update(p);
}
void Insert(int& p,int val)
{
if(!p){ p=New(val); return; }
if(val==a[p].val){ a[p].cnt++,Update(p); return; }
if(val<a[p].val)
{
Insert(a[p].l,val);
if(a[p].dat<a[a[p].l].dat) zig(p);
}
else
{
Insert(a[p].r,val);
if(a[p].dat<a[a[p].r].dat) zag(p);
}
Update(p);
}
int GetPre(int val)
{
int ans=1;
int p=root;
while(p)
{
if(val==a[p].val)
{
if(a[p].l>0)
{
p=a[p].l;
while(a[p].r>0) p=a[p].r;
ans=p;
}
break;
}
if(a[p].val<val && a[p].val>a[ans].val) ans=p;
p=val<a[p].val?a[p].l:a[p].r;
}
return a[ans].val;
}
int GetNext(int val)
{
int ans=2;
int p=root;
while(p)
{
if(val==a[p].val)
{
if(a[p].r>0)
{
p=a[p].r;
while(a[p].l>0) p=a[p].l;
ans=p;
}
break;
}
if(a[p].val>val && a[p].val<a[ans].val) ans=p;
p=val<a[p].val?a[p].l:a[p].r;
}
return a[ans].val;
}
void Remove(int& p,int val)
{
if(!p) return;
if(val==a[p].val)
{
if(a[p].cnt>1){ a[p].cnt--,Update(p); return; }
if(a[p].l || a[p].r)
{
if(!a[p].r || a[a[p].l].dat>a[a[p].r].dat)
zig(p),Remove(a[p].r,val);
else zag(p),Remove(a[p].l,val);
Update(p);
}
else p=0;
return;
}
val<a[p].val?Remove(a[p].l,val):Remove(a[p].r,val);
Update(p);
}
int main()
{
srand(time(0));
Build();
scanf("%d",&n);
while(n--)
{
int opt,x;
scanf("%d %d",&opt,&x);
switch(opt)
{
case 1:Insert(root,x);break;
case 2:Remove(root,x);break;
case 3:printf("%d\n",GetRankByVal(root,x)-1);break;
case 4:printf("%d\n",GetValByRank(root,x+1));break;
case 5:printf("%d\n",GetPre(x));break;
case 6:printf("%d\n",GetNext(x));break;
}
}
return 0;
}


