递归函数的运用
计算组合数
一、利用n!计算
1. 设计思想:
利用组合数公式计算,通过对n的阶乘进行递归,实现求n!。通过调用n!,利用如下公式计算:

2.程序流程图:


3.源程序代码:
import java.util.Scanner; public class Zuheshu { public static void main(String[] args) { // TODO Auto-generated method stub Scanner in=new Scanner(System.in); System.out.println("m 应大于n"); System.out.println("格式为c(m,n)"); System.out.println("m:"); int m=in.nextInt(); System.out.println("n:"); int n=in.nextInt(); zhuhe(n,m); System.out.println(""); } public static int jiecheng(int n) { if(n==1){return 1;} return n*jiecheng(n-1); } public static void zhuhe(int n,int m) { int sum; sum=jiecheng(m)/(jiecheng(n)*jiecheng(m-n)); System.out.print("c"+"("+m+","+n+")"+"="+sum); } }
4.程序截图:

二、用递推的方法用杨辉三角形计算
1.设计思想:
杨辉三角可以反映组合数的值,例如杨辉三角中第六排三列为10,即对应组合数c(5,2);通过递归建立杨辉三角,
再通过杨辉三角输出组合数值。
2.程序流程图:


3.源代码:
import java.util.Scanner; public class Zuheshu_1 { public static void main(String[] args) { // TODO Auto-generated method stub Scanner in=new Scanner(System.in); System.out.println("m 应大于n"); System.out.println("格式为c(m,n)"); System.out.println("m:"); int m=in.nextInt(); System.out.println("n:"); int n=in.nextInt(); System.out.println("c"+"("+m+","+n+")"+"="+dituiYanhui(n,m)); } public static int dituiYanhui(int n,int m) { int a[][]=new int[m+1][m+1]; for(int i=0;i<m+1;i++) { for(int j=i+1;j<m+1;j++) { a[i][j]=0; } for(int j=0;j<=i;j++) { if(j==0){ a[i][j]=1;} else { a[i][j]=a[i-1][j-1]+a[i-1][j]; } } } return a[m][n]; } }
4.程序截图:

三、使用递归的方法用组合数递推公式计算
1.设计思想:通过对组合数递推公式的递归实现,输出组合数的值
2.程序流程图:

3.源程序代码:
import java.util.Scanner; public class Zuheshu_2 { public static void main(String[] args) { // TODO Auto-generated method stub Scanner in=new Scanner(System.in); System.out.println("m 应大于n"); System.out.println("格式为c(m,n)"); System.out.println("m:"); int m=in.nextInt(); System.out.println("n:"); int n=in.nextInt(); System.out.println("c"+"("+m+","+n+")"+"="+digui(n,m)); } public static int digui(int n,int m) { if(n>m||n<0||m<0){return 0;} if(n==1){return m;} if(n==m){return 1;} return digui(n-1,m-1)+digui(n,m-1); } }
4.程序截图:

递归编程解决汉罗塔问题
1.设计思想:
无论有多少个盘子,始终都有n个盘子从peg1移动到peg3,有n-1个盘子从peg3移动到peg2,也有n-1个盘子从peg1到peg2,
由此进行递归运算,解决问题。
2.程序流程图:

3.源代码:
import java.util.Scanner; public class HanLuo_1 { static int m=0; public static void main(String[] args) { // TODO Auto-generated method stub Scanner in = new Scanner(System.in); System.out.println("输入圆盘个数:"); int n=in.nextInt(); String a= "peg1"; String b= "peg2"; String c= "peg3"; move(n,a,b,c); System.out.println("共执行"+m+"次"); } public static void move(int n,String a,String b,String c) { if(n==1) { System.out.println("第"+(++m)+"次移动"+":"+n+"号圆盘"+a+"-->"+c); } else { move(n-1,a,c,b); System.out.println("第"+(++m)+"次移动"+":"+n+"号圆盘"+a+"-->"+c); move(n-1,b,a,c); } } }
4.程序截图:

使用递归方式判断某个字串是否是回文
1.设计思想:先输入一段字符串。利用String.charAT()函数得到字符串的各个位上的字符,进行比较。
在调用自己进行递归。
2.程序流程图:
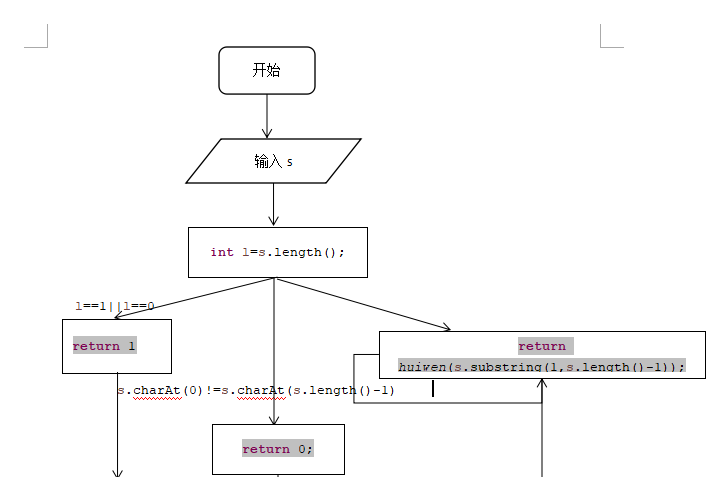

3.源代码:
import java.util.Scanner; public class HuiWenString { public static void main(String[] args) { // TODO Auto-generated method stub Scanner in = new Scanner(System.in); String s=in.nextLine(); if(huiwen(s)==1){ System.out.print("这是回文字符串"); } else { System.out.print("这不是回文字符串"); } } public static int huiwen(String s) { int l=s.length(); if(l==1||l==0) { return 1; } if(s.charAt(0)!=s.charAt(s.length()-1)) { return 0; } return huiwen(s.substring(1,s.length()-1)); } }
4程序截图:




 浙公网安备 33010602011771号
浙公网安备 33010602011771号