BFPRT算法

首先讲一下bfprt算法是干嘛的？

bfprt算法是用来求数组中第k小的元素的算法，bfprt算法可以在O（n）时间内求出答案。

算法思想：

对于求数组中第k小的元素的问题，我们已经有很好的常规算法了，这个算法在最好的情况下时间复杂度是O（n），但在最坏的情况下是O（n^2）的，其实bfprt算法就是在这个基础上改进的。

常规解法：

我们随机在数组中选择一个数作为划分值（number），然后进行快排的partation过程（将小于number的数放到数组左边，等于number的数放到数组中间，大于number的数放到数组右边），然后判断k与等于number区域的相对关系，如果k正好在等于number区域，那么数组第k小的数就是number，如果k在等于number区域的左边，那么我们递归对左边再进行上述过程，如果k在等于number区域的右边，那我们递归对右边再进行上述过程。

对于常规解法，我们分析一下它的时间复杂度：

递归函数复杂度计算：

T(N)=aT(N/b)+o(N^d);
当log(b,a)>d时 复杂度为O（N^log(b,a）);
当log(b,a)=d时 复杂度为O（N^dlog(2,N));
当log(b,a)<d时 复杂度为O（N^d);
N为样本数据个数 即数组中元素的个数。
N/b为将这N个数划分为更小的部分，每个部分的样本数据个数，一般为均分，那么b等于2。
a为划分为多个部分后，小部分执行的次数。
d为递归函数调用完成后剩下的操作的时间复杂度。

对于最好的情况：每次所选的number正好在数组的正中间，那么上式中a等于1，b等于2，对于partation过程，时间复杂度是O（n），所以d等于1。所以T（N）= T（N/2）+ O（N），此时 log( 2 , 1 ) < 1，故时间复杂度为O（N）。【第一次是O(N), 第二次是O(N/2), 第三次是 O(N/4) ... 第N次是O(N/N)，总时间复杂度就是O(N + N/2 + N/4....+1) = O(2N-1)=O(N)】

对于最坏情况：每次所选的number正好在数组最边上，那么时间复杂度为O（N ^ 2）。【第一次是O(N), 第二次是O(N-1), 第三次是 O(N-2) ... 第N次是O(N-N)，总时间复杂度就是O(N + (N-1) + (N-2)....+(N-N))=O(N^2)】

bfprt算法就是在这个number上做文章，bfprt算法能够保证每次所选的number在数组的中间位置，那么时间复杂度就是O（N）。

bfprt解法：

bfprt解法和常规解法唯一不同的就是在number的选取上，其他地方一模一样，所以我们只讲选取number这一过程。

第一步：我们将数组每5个相邻的数分成一组，后面的数如果不够5个数也分成一组。

第二步：对于每组数，我们找出这5个数的中位数，将所有组的中位数构成一个median数组（中位数数组）。

第三步：我们再求这个中位数数组中的中位数，此时所求出的中位数就是那个number。

第四步：通过这个number进行partation过程，下面和常规解法就一样了。

接下来我们分析一下为什么bfprt算法每次选number的时候都能够在数组的中间位置。

我们假设这就是分出来的每5个数的小组，每一列代表一个小组。

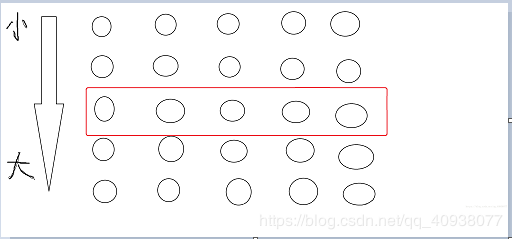
图中红框内的数我们假设就是每一组的中位数。我们假设总数组的数字个数是N，那么中位数数组中数字的个数就是 N / 5 。

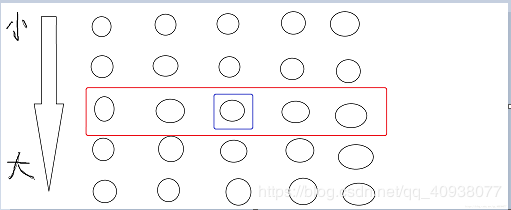
我们假设用蓝框框起来的数是中位数数组的中位数（divide），那么由中位数的性质可知，中位数数组中有一半的数比这个divide大，所以总共有 N / 10个数比这个divide大。

用紫色框框出的数肯定也是比divide大，所以至少有N / 10 + ( 2N ) / 10 = ( 3N ) / 10 个数比divide大，那么以divide为划分的partation过程能够使得divide在数组的靠近中间的位置，最坏情况也能够在数组的 ( 3N ) / 10 或者 ( 7N ) / 10 的位置。时间复杂度为O（N）。
讲一下BFPRT的空间复杂度，select分治过程用到递归，需要栈空间存储，递归次数即是栈空间大小，由于每次只处理划分后的一半，因此最差情况需要递归log（N）次，空间复杂度为log（N）。

代码如下：

"""
BFPRT算法，简称 TOP K 问题，用来求数组中第k小元素的算法
    - 可以在O（n）时间内求出答案
"""
class Solution:
    def get_median(self, nums):
        '''计算5个数的中位数'''
        begin, end = 0, len(nums) - 1

        sum = begin + end
        mid = sum // 2 + sum % 2  # 这个地方加上sum%2是为了确保偶数个数时我们求的是中间两个数的后一个
        return sorted(nums)[mid]  # 常量级别，影响不大，也可改用插入排序

    def BFPRT(self, nums, left, right):
        '''选择partition基准: 划分每5个一组，求每组的中位数'''
        num = right-left + 1
        offset = 0 if num % 5 == 0 else 1  # 最后如果剩余的数不足5个，我们也将其分成一个小组，和前面同等对待
        group = num//5 + offset

        median = []  # 中位数数组
        for i in range(group):
            begin = left + i * 5
            end = begin + 4
            Median = self.get_median(nums[begin:min(end, right) + 1])
            median.append(Median)
        # return self.get_median(median)  # 这里是求中位数数组的中位数，再调用getmedian不就行了，为啥有的人还要用下面递归select，虽然也是正确的，但直接getmedian快一点啊。2022-05-19: median可能很大 sorted() 复杂度就不是常数级别了
        return select(median, 0, groups-1, groups//2)  # 求出生成好的median数组的中位数，作为partation函数的划分值

    def partition(self, nums, left, right, base):
        '''将基准base归位'''
        if left >= right:
            return

        temp = nums[base]
        nums[base], nums[right] = nums[right], nums[base]  # 和尾部节点交换

        max_index = left
        for i in range(left, right):
            if nums[i] <= temp:
                nums[max_index], nums[i] = nums[i], nums[max_index]
                max_index += 1
        nums[max_index], nums[right] = nums[right], nums[max_index]
        return max_index

    def select(self, nums, left, right, K):
        '''快速选择过程'''
        if left == right:
            return nums[left]

        base = self.BFPRT(nums, left, right)                              # 选择基准
        base_index = self.partition(nums, left, right, nums.index(base))  # 基准归位

        if base_index == K:   # 判断目前已归位的基准，是不是第K位
            return nums[base_index]
        elif base_index > K:  # 递归左半部分
            return self.select(nums, left, base_index - 1, K)
        else:                 # 递归右半部分
            return self.select(nums, base_index + 1, right, K)

    def MoreThanHalfNum_Solution(self, numbers):
        if not numbers:
            return 0

        left, right = 0, len(numbers) - 1
        length = len(numbers)
        K = right // 2
        ans = self.select(numbers, left, right, right - K + 1)  # 第K大，也是第N-K+1小

        # 核实
        cnt = 0
        for x in numbers:
            if x == ans:
                cnt += 1
                if cnt == length // 2 + 1:
                    return ans
        return 0


# 数组中出现次数超过一半的数字
s = Solution()
ans = s.MoreThanHalfNum_Solution([1, 2, 3, 2, 2, 2, 5, 4, 2])
print(ans)

https://blog.csdn.net/qq_40938077/article/details/81213820#commentBox