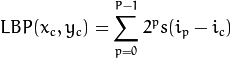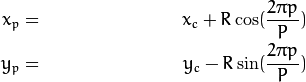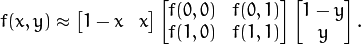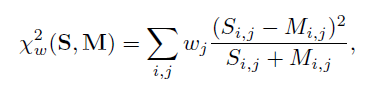图像物体检測识别中的LBP特征
图像物体检測识别中的LBP特征
1 引言
之前讲了人脸识别中的Haar特征，本文则关注人脸检測中的LBP特征。说是对于人脸检測的，事实上对于其它物体也能检測，仅仅需改动训练数据集就可以。
所以本文的题目是物体检測识别，比方能够检測是否汽车是否有车牌号等。
在opencv实现的haar特征的人脸识别算法中，LBP特征也被支持。
haar特征的博文链接：http://blog.csdn.net/stdcoutzyx/article/details/34842233。
2 LBP的历史
1996年，Ojala老大爷搞出了LBP特征，也即參考文献1。当时好像并未引发什么波澜。到了2002年的时候，老大爷又对LBP的特性进行了总结。产生了參考文献2。这篇文献眼下为止引用数目4600+。足见其分量之重了。
到了2004年的时候，Ahonen将LBP特征首次用于人脸检測。即參考文献3。因为该特征的简单易算性，尽管其整体效果不如Haar特征，但速度则快于Haar。所以也得到了广泛的使用。
2007年的时候，中科院的一帮大神将Haar特征计算的积分图方法引入进来，产生了多尺度的LBP特征。也即參考文献4。使得LBP在人脸识别的检測率上又提高了不少。
LBP特征与多尺度LBP以及LBP在人脸识别中的应用就是本文的主要内容。
3 LBP特征
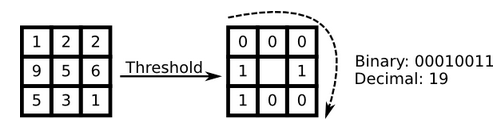
言归正传。什么是LBP特征呢？LBP，是Local Binary Pattern（局部二值模式）的缩写。其定义例如以下：
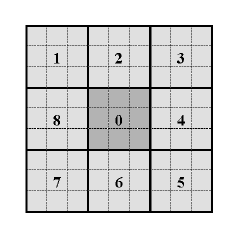
以邻域中心像素为阈值，将相邻的8个像素的灰度值与其进行比較，若周围像素值大于中心像素值。则该像素点的位置被标记为1，否则为0。这样。3x3邻域内的8个点经比較可产生8位二进制数（通常转换为十进制数即LBP码，共256种），即得到该邻域中心像素点的LBP值，并用这个值来反映该区域的纹理信息。
下图反应了某个像素的详细的LBP特征值的计算过程。须要注意的是，LBP值是依照顺时针方向组成的二进制数。
用公式来定义的话。例如以下所看到的：
当中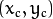
s(x)是符号函数，定义例如以下：
4 LBP特征的圆形化改进
原始论文[1]中定义了基础LBP后，还定义了一种改进方法，即圆形化LBP。
主要的 LBP算子的最大缺陷在于它仅仅覆盖了一个固定半径范围内的小区域，这显然不能满足不同尺寸和频率纹理的须要。
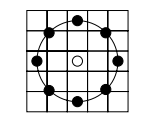
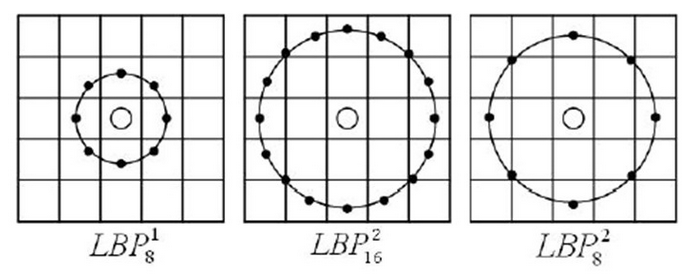
为了适应不同尺度的纹理特征。并达到灰度和旋转不变性的要求。Ojala等对 LBP 算子进行了改进，将 3×3邻域扩展到随意邻域。并用圆形邻域取代了正方形邻域。改进后的 LBP 算子同意在半径为 R 的圆形邻域内有随意多个像素点。从而得到了诸如半径为R的圆形区域内含有P个採样点的LBP算子。
比方下图定了一个5x5的邻域：
上图内有八个黑色的採样点，每一个採样点的值能够通过下式计算：
当中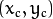
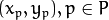
通过上式能够计算随意个採样点的坐标，可是计算得到的坐标未必全然是整数，所以能够通过双线性插值来得到该採样点的像素值：
下图列举了几种不同半径不同採样点的LBP算子例子。
5 LBP特征的再转化
经过LBP算子的计算后。图像上相应于每一个像素都会有一个LBP特征值。假设LBP特征计算时採样点是8个的话，那么LBP特征值的范围也是0~255。也能够表示成一张图像。称之为LBP图谱。例如以下图所看到的：
上图中，上面一行是原图，以下一行是LBP图谱。能够看到LBP特征的一个优势，就是LBP对光照有非常好的鲁棒性。
可是，在实际应用中，并不使用LBP图谱做特征。那使用什么哩？
对于八採样点的LBP算子来说，特征值范围为0~255，对每一个特征值进行统计，比方得到特征值为1的LBP值有多少个、特征值为245的LBP值有多少个等等。这样就形成了一个直方图，该直方图有256个bin，即256个分量，也能够把该直方图当做一个长度为256的向量。
假设直接使用该向量的话。那么对八採样点的LBP算子来说，一张图片至多会形成一个256长度的一个向量，这样位置信息就所有丢失了，会造成非常大的精度问题。
所以在实际中还会再有一个技巧，就是先把图像分成若干个区域。对每一个区域进行统计得到直方图向量，再将这些向量整合起来形成一个大的向量。下图就将一张人脸图像分成了7x7的子区域。
6 LBP特征的使用
本文介绍两个LBP特征的使用。其一是图像类似度计算，其二是人脸检測。
6.1 图像类似度计算
每一个图像都能够使用一个LBP特征向量来表示。图像的类似度就能够使用向量的类似度来计算。
向量的类似度计算方法有非常多。比方余弦、距离等。在文献3中。这种基于直方图向量的类似度计算方法给出了三种，例如以下图所看到的。
上图中公式仅仅是针对一个直方图的。使用中还会将图像分为多个区域分别计算直方图。所以在实际使用中，还可对不同区域进行加权。
6.2 特定人脸检測
在上述计算图像类似度的公式中。须要对每一个分量计算一个值（差值、最小值等），然后将这些值累加。我们还能够这样考虑，不将每一个分量计算出的值累加。而是形成一个新的向量。临时称之为差异向量。
这样就能够针对特定人脸进行检測了。
详细训练方法是这样：
a) 首先准备训练集，正例是同一个人的人脸的两张图像的差异向量。负例是不同人的人脸的两张图像的差异向量。
b) 然后。使用如Adaboost、SVM、朴素贝叶斯等分类方法对训练集进行训练，得到分类模型。
在測试时，假设有一张图像A，如今须要推断图像B与图像A中的人脸是否是同一个人。那么首先计算出两张图像的差异向量，然后使用训练得到的分类模型对其进行分类。假设分类为正，则是同一个人。当然。前提假设是图像A与图像B都是人脸图像。
7 LBP特征降维
一个LBP算子能够产生不同的二进制模式，对于半径为R的圆形区域内含有P个採样点的LBP算子将会产生2^P种模式。非常显然，随着邻域集内採样点数的添加，二进制模式的种类是急剧添加的。比如：5×5邻域内20个採样点，有2^20＝1,048,576种二进制模式。如此多的二值模式不管对于纹理的提取还是对于纹理的识别、分类及信息的存取都是不利的。
同一时候，过多的模式种类对于纹理的表达是不利的。
比如，将LBP算子用于纹理分类或人脸识别时，常採用LBP模式的统计直方图来表达图像的信息。而较多的模式种类将使得数据量过大，且直方图过于稀疏。因此。须要对原始的LBP模式进行降维，使得数据量降低的情况下能最好的代表图像的信息。
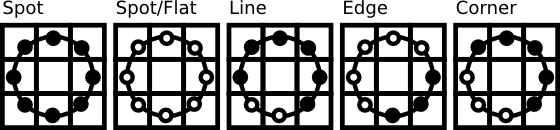
为了解决二进制模式过多的问题，提高统计性，Ojala提出了採用一种“等价模式”（Uniform Pattern）来对LBP算子的模式种类进行降维。Ojala等觉得，在实际图像中，绝大多数LBP模式最多仅仅包括两次从1到0或从0到1的跳变。因此，Ojala将“等价模式”定义为：当某个LBP所相应的循环二进制数从0到1或从1到0最多有两次跳变时。该LBP所相应的二进制就称为一个等价模式类。如00000000（0次跳变），00000111（仅仅含一次从0到1的跳变）。10001111（先由1跳到0，再由0跳到1，共两次跳变）都是等价模式类。除等价模式类以外的模式都归为还有一类。称为混合模式类，比如10010111（共四次跳变）。比方下图给出了几种等价模式的示意图。
通过这种改进。二进制模式的种类大大降低。而不会丢失不论什么信息。
模式数量由原来的2P种降低为 P ( P-1)+2种，当中P表示邻域集内的採样点数。
对于3×3邻域内8个採样点来说，二进制模式由原始的256种降低为58种。这使得特征向量的维数更少，而且能够降低高频噪声带来的影响。
由上可见。等价模式降维的理论基础是至多包括两次跳变的模式的数目占所有模式的大多数。实验也表明，普通情况下。基础LBP特征中，至多包括两次跳变的模式的数目占了所有模式数目的90%。
8 多尺度LBP
本节主要是參考文献4的成果。
基本LBP是计算的单个像素与其相邻像素的差值信息。它捕捉的是微观特征。可是不能捕捉宏观上的特征。文献4在此方面进行了改进。它提出能够将LBP算子等比例放大，计算区域与区域之间的差值信息。例如以下图所看到的：
上图就是放大3倍后的LBP算子。这时，中心元素变为了0区域9个像素的像素和，该区域的LBP特征值就变为0区域和其它区域的像素和之间的计算了。在此须要注意的是。此时的LBP特征针对的是一个区域而不是一个像素了。在计算像素和之差的时候。能够使用Haar特征时提到的积分图方法进行加速计算。
多尺度模式下。等价模式类降维的理论基础不复存在。
那么，它是怎样降维的呢？
论文中提到的方法是直接採用统计的方法对不同尺度的LBP算子的模式进行统计，选取占比例较高的模式。而不是利用跳变规则。
9 总结
LBP特征与Haar特征尽管计算方法差异非常大。但它们都有一个共同的目标。那就是对图像的信息进行表示，从而使图像的所存储的信息能更充分的被算法所利用。
图像中像素与LBP特征、Haar特征之间的关系比較类似于文本分析中字与词之间的关系。文本分析中，假设想要获得语义理解的话。那应该须要处理句子、短语、词语等，单单分析字是远远不够的。
图像处理中，要想得到丰富的图像包括的信息，单单分析像素也是不够的。
本文与Haar特征的那篇博文都使用到了Adaboost分类器。但其使用的目的却全然不一样，Haar特征中使用Adaboost是对有脸和无脸的图像进行分类，而本文是对是不是同一个人的脸进行分类。从这就能够感觉的到，非常多机器学习问题事实上本质上都能够化为分类问题，当然。还有一大类是回归问题。
个人觉得本篇博文对LBP的讨论已经够全面了。有想深入学习的同学请阅读參考文献，欢迎来信讨论。
转载请注明：http://blog.csdn.net/stdcoutzyx/article/details/37317863
參考文献
[1]. Ojala, T., Pietik¨ainen, M., Harwood, D.: A comparative study of texture measures with classification based on feature distributions. Pattern Recognition 29 (1996)51–59.
[2]. Ojala T, Pietikainen M, Maenpaa T. Multiresolution gray-scale and rotation invariant texture classification with local binary patterns[J]. Pattern Analysis and Machine Intelligence, IEEE Transactions on, 2002, 24(7):
971-987.
[3]. Ahonen T, Hadid A, Pietikäinen M. Face recognition with local binary patterns[M]//Computer vision-eccv 2004. Springer Berlin Heidelberg, 2004: 469-481.
[4]. Liao S, Zhu X, Lei Z, et al. Learning multi-scale block local binary patterns for face recognition[M]//Advances in Biometrics. Springer Berlin Heidelberg, 2007: 828-837.
[5]. http://blog.csdn.net/smartempire/article/details/23249517
