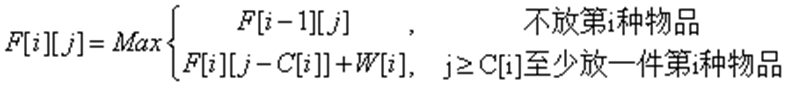包子凑数(dp 0-1、完全背包)【背包问题】
包子凑数(蓝桥杯)
题目描述
小明几乎每天早晨都会在一家包子铺吃早餐。他发现这家包子铺有N种蒸笼,其中第i种蒸笼恰好能放Ai个包子。每种蒸笼都有非常多笼,可以认为是无限笼。
每当有顾客想买X个包子,卖包子的大叔就会迅速选出若干笼包子来,使得这若干笼中恰好一共有X个包子。比如一共有3种蒸笼,分别能放3、4和5个包子。当顾客想买11个包子时,大叔就会选2笼3个的再加1笼5个的(也可能选出1笼3个的再加2笼4个的)。
当然有时包子大叔无论如何也凑不出顾客想买的数量。比如一共有3种蒸笼,分别能放4、5和6个包子。而顾客想买7个包子时,大叔就凑不出来了。
小明想知道一共有多少种数目是包子大叔凑不出来的。第一个例子:
2
4
5输出:
6
输入
第一行包含一个整数N。(1 <= N <= 100)
以下N行每行包含一个整数Ai。(1 <= Ai <= 100)输出
一个整数代表答案。如果凑不出的数目有无限多个,输出INF。
样例输入
2
4
6
样例输出INF
提示对于样例1,凑不出的数目包括:1, 2, 3, 6, 7, 11。
对于样例2,所有奇数都凑不出来,所以有无限多个。
思路:
题目说明了包子笼数假设有无限个 想到是完全背包(所有物品种类数假设有无限个)
补充:
1、0-1背包dp: (每种物品只有1个)
例题:
有重量分别为16 15 15 的三个物品 其价值分别为 30 25 25 要将他们装进承载重量最大为30的包中 计算最大价值是多少?(用dp解决这个问题)
s[i][j] 表示 遍历第i个物品 剩余背包容量为 j
代码如下:
#include<bits/stdc++.h> using namespace std; int w[5]={16,15,15},v[5]={30,25,25},dp[55][55]; int main() { int n=3,m=30,maxx=-100; for(int i=0;i<n;i++){ for(int j=0;j<=m;j++){ if(j>=w[i]){ dp[i][j]=max(dp[i-1][j],dp[i-1][j-w[i]]+v[i]); } else{ dp[i][j]=dp[i-1][j]; } if(dp[i][j]>maxx){ //或者是将判断删去 改为直接最后输出dp[n-1][m]; maxx=dp[i][j]; } } } printf("%d\n",maxx); return 0; }
2、完全背包dp:
例题 :
重量分别为2 4 8 3价值分别为5 9 18 9 的四件物品 每种物品数量有无限个 背包容量为10 计算最大价值:
· 注意和0-1 背包的区别:
例如:有重量为2的物品, dp[i][2]的时候放了一件了,当dp[i][4]的时候,dp[i][4]=max(dp[i-1][4],dp[i][4-2]+w[i]) 最多放一件
代码如下:
#include<bits/stdc++.h> using namespace std; const int maxn=105; int dp[maxn][55]; int w[maxn+5],v[maxn+5]; int n,m; int main() { int i,j,k; while(~scanf("%d %d",&n,&m)){ memset(dp,0,sizeof(dp)); for(i=1;i<=n;i++){ scanf("%d %d",&w[i],&v[i]); } for(i=1;i<=n;i++){ for(j=0;j<=m;j++){ if(j>=w[i]){ dp[i][j]=max(dp[i-1][j],dp[i][j-w[i]]+v[i]);//注意和01背包的区别,这里是 dp[i][j-need[i]]+value[i] } else{ dp[i][j]=dp[i-1][j]; } } } printf("%d\n",dp[n-1][m]); } return 0; }
这个题和上面有点差别 没有价格的区别所以我开始就把物品重量当成价值 最后判断背包是否被填满 但是数目大了就会错误 不得不放弃 看了@ Statusrank的讲解才明白我想复杂了 链接(点击)
先遍历每个a[i] 然后将对应的dp值改变
往后再遍历的时候 直接dp[j]=dp[ j-a[i] ]
例如 :
a1=4,a2=5:前提 令dp[0]=1(下面解释为甚麽)
先遍历4 将 4和其倍数的值变为1 因为dp[j]=dp[ j-a[i] ]
当j=4时 dp[4]=dp[4-a[1]]=dp[0]=1;
再遍历5的时候会将5 的倍数变为1(同理)
同时 当j=9时: dp[9]=dp[9-a[2]]=dp[4]=1; 也会将其他5 和4组成的数的dp赋值为1
AC代码:
#include<bits/stdc++.h>
using namespace std;
const int MAX=1e5;
int dp[MAX+5],a[105];
int main()
{
int n,count=0;
scanf("%d",&n);
for(int i=0;i<n;i++){
scanf("%d",&a[i]);
if(a[i]%2==0){
count++;
}
}
if(count==n){
printf("INF\n");
}
else{
count=0;
dp[0]=1;
for(int i=0;i<n;i++){
for(int j=a[i];j<=MAX+5;j++){
dp[j]=max(dp[j],dp[j-a[i]]);
}
}
for(int i=1;i<MAX+5;i++){
if(dp[i]==0){
count++;
}
}
printf("%d\n",count);
}
return 0;
}