HMM代码实践
本文主要转载于：http://www.52nlp.cn/hmm-learn-best-practices-eight-summary
这个文章是边看边实践加上自己的一些想法生成的初稿。。。。。
状态转移概率：M^2个状态转移
初始概率：pi向量，起始日天气的（或可能的）情况。（初始概率）
状态：三个状态——晴天，多云，雨天。
pi向量：定义系统初始化时每一个状态的概率。
状态转移矩阵：给定前一天天气情况下的当前天气概率。
任何一个可以用这种方式描述的系统都是一个马尔科夫过程。
关于假设，重要的一点是状态转移矩阵并不随时间的改变而改变——这个矩阵在整个系统的生命周期中是固定不变的。
三、隐藏模式（Hidden Patterns）
天气和水藻的状态是紧密相关的。在这个例子中我们有两组状态，观察的状态（水藻的状态）和隐藏的状态（天气的状态）。我们希望为隐士设计一种算法，在不能够直接观察天气的情况下，通过水藻和马尔科夫假设来预测天气。
一个更实际的问题是语音识别，我们听到的声音是来自于声带、喉咙大小、舌头位置以及其他一些东西的组合结果。所有这些因素相互作用产生一个单词的声音
需要着重指出的是，隐藏状态的数目与观察状态的数目可以是不同的。一个包含三个状态的天气系统（晴天、多云、雨天）中，可以观察到4个等级的海藻湿润情况（干、稍干、潮湿、湿润）；
在这种情况下，观察到的状态序列（海藻）与隐藏（天气）过程有一定的概率关系
2、隐马尔科夫模型（Hidden Markov Models）
隐藏状态和观察状态之间的连接表示：在给定的马尔科夫过程中，一个特定的隐藏状态生成特定的观察状态的概率
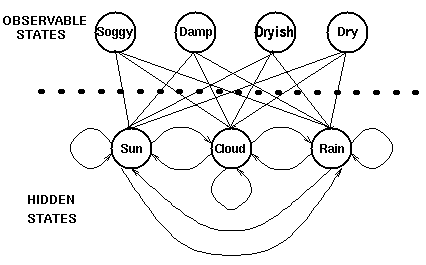
很清晰的表示了‘进入’一个观察状态的所有概率之和为1,上面这个例子中就是Pr(Obs|Sun)，Pr(Obs|Cloud) 及 Pr(Obs|Rain)之和。
除了定义了马尔科夫过程的概率关系，我们还有另一个矩阵，定义为混淆矩阵（confusion matrix）
一个隐藏状态后得到的观察状态的概率。
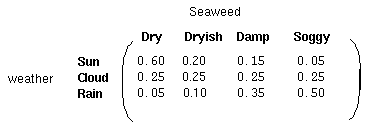
注意矩阵的每一行之和是1。
我们使用一个隐马尔科夫模型（HMM）对这些例子建模。
* 隐藏状态：一个系统的（真实）状态，可以由一个马尔科夫过程进行描述（例如，天气）。
* 观察状态：在这个过程中‘可视’的状态（例如，海藻的湿度）。
* pi向量：包含了（隐）模型在时间t=1时一个特殊的隐藏状态的概率（初始概率）。
* 状态转移矩阵：包含了一个隐藏状态到另一个隐藏状态的概率
* 混淆矩阵：包含了给定隐马尔科夫模型的某一个特殊的隐藏状态，观察到的某个观察状态的概率。
因此一个隐马尔科夫模型是在一个标准的马尔科夫过程中引入一组观察状态，以及其与隐藏状态间的一些概率关系。
四、隐马尔科夫模型（Hidden Markov Models）
1、定义（Definition of a hidden Markov model）
一个隐马尔科夫模型是一个三元组（pi, A, B）。
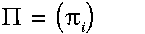：初始化概率向量；
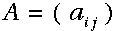：状态转移矩阵；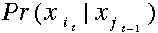
：混淆矩阵；
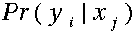
在状态转移矩阵及混淆矩阵中的每一个概率都是时间无关的——也就是说，当系统演化时这些矩阵并不随时间改变。实际上，这是马尔科夫模型关于真实世界最不现实的一个假设。
2、应用
一旦一个系统可以作为HMM被描述，就可以用来解决三个基本问题。
其中前两个是模式识别的问题：给定HMM求一个观察序列的概率（评估）；搜索最有可能生成一个观察序列的隐藏状态序列（解码）。第三个问题是给定观察序列生成一个HMM（学习）。
a) 评估（Evaluation）
我们有一些描述不同系统的隐马尔科夫模型（也就是一些( pi,A,B)三元组的集合）及一个观察序列
我们想知道哪一个HMM最有可能产生了这个给定的观察序列(海藻)。例如，对于海藻来说，我们也许会有一个“夏季”模型和一个“冬季”模型，因为不同季节之间的情况是不同的——我们也许想根据海藻湿度的观察序列来确定当前的季节。
我们使用前向算法（forward algorithm）来计算给定隐马尔科夫模型（HMM）后的一个观察序列的概率,选择最合适的隐马尔科夫模型(HMM)。
在语音识别中这种类型的问题发生在当一大堆数目的马尔科夫模型被使用，并且每一个模型都对一个特殊的单词进行建模时。一个观察序列从一个发音单词中形成，并且通过寻找对于此观察序列最有可能的隐马尔科夫模型（HMM）识别这个单词。
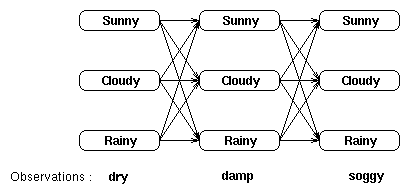
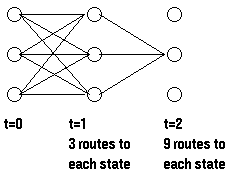
网格中的每一列都显示了可能的的天气状态，并且每一列中的每个状态都与相邻列中的每一个状态相连。而其状态间的转移都由状态转移矩阵提供一个概率。在每一列下面都是某个时间点上的观察状态，给定任一个隐藏状态所得到的观察状态的概率由混淆矩阵提供。
可以看出，一种计算观察序列概率的方法是找到每一个可能的隐藏状态，并且将这些隐藏状态下的观察序列概率相加。对于上面那个（天气）例子，将有3^3 = 27种不同的天气序列可能性，因此，观察序列的概率是：
Pr(dry,damp,soggy | HMM) = Pr(dry,damp,soggy | sunny,sunny,sunny) + Pr(dry,damp,soggy | sunny,sunny ,cloudy) + Pr(dry,damp,soggy | sunny,sunny ,rainy) + . . . . Pr(dry,damp,soggy | rainy,rainy ,rainy)
用这种方式计算观察序列概率极为昂贵，特别对于大的模型或较长的序列，因此我们可以利用这些概率的时间不变性来减少问题的复杂度。
b) 解码（ Decoding）
给定观察序列搜索最可能的隐藏状态序列（天气）。
我们使用Viterbi 算法（Viterbi algorithm）确定（搜索）已知观察序列及HMM下最可能的隐藏状态序列。
Viterbi算法（Viterbi algorithm）的另一广泛应用是自然语言处理中的词性标注
在词性标注中，句子中的单词是观察状态，词性（语法类别）是隐藏状态（注意对于许多单词，如wind，fish拥有不止一个词性）。
对于每句话中的单词，通过搜索其最可能的隐藏状态，我们就可以在给定的上下文中找到每个单词最可能的词性标注。
C）学习（Learning）
根据观察序列生成隐马尔科夫模型。
第三个问题，也是与HMM相关的问题中最难的，根据一个观察序列（来自于已知的集合），以及与其有关的一个隐藏状态集，估计一个最合适的隐马尔科夫模型（HMM)
也就是确定对已知序列描述的最合适的（pi,A,B）三元组。
当矩阵A和B不能够直接被（估计）测量时，前向-后向算法（forward-backward algorithm）被用来进行学习（参数估计），这也是实际应用中常见的情况。
3、总结（Summary）
由一个向量和两个矩阵(pi,A,B)描述的隐马尔科夫模型对于实际系统有着巨大的价值，虽然经常只是一种近似，但它们却是经得起分析的。隐马尔科夫模型通常解决的问题包括：
1. 对于一个观察序列匹配最可能的系统——评估，使用前向算法（forward algorithm）解决；
2. 对于已生成的一个观察序列，确定最可能的隐藏状态序列——解码，使用Viterbi 算法（Viterbi algorithm）解决；
3. 对于已生成的观察序列，决定最可能的模型参数——学习，使用前向-后向算法（forward-backward algorithm）解决。
前向算法1：
计算观察序列的概率
1.穷举搜索
在模型参数（pi, A, B)已知，我们想找到观察序列的概率，设连续3天海藻湿度的观察结果是（干燥、湿润、湿透）
2.使用递归降低问题复杂度：
我们首先定义局部概率（partial probability）,它是到达网格中的某个中间状态时的概率
我们可以将计算到达网格中某个中间状态的概率作为所有到达这个状态的可能路径的概率求和问题。
例如，t=2时位于“多云”状态的局部概率通过如下路径计算得出：
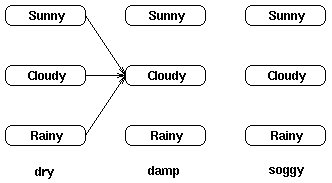
我们定义t时刻位于状态j（多云）的局部概率为at(j)——这个局部概率计算如下：
t ( j )= Pr( 观察状态 | 隐藏状态j ) x Pr(t时刻所有指向j状态的路径）
对于这些最终局部概率求和等价于对于网格中所有可能的路径概率求和
t=1时的局部概率等于当前状态的初始概率乘以相关的观察概率：
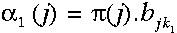
为了计算到达某个状态的所有路径的概率，我们可以计算到达此状态的每条路径的概率并对它们求和，例如：
此，我们可以通过t-1时刻的局部概率定义t时刻的‘s，即：
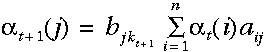i
2d.降低计算复杂度
我们首先通过计算局部概率（‘s）降低计算整个概率的复杂度，局部概率表示的是t时刻到达某个状态s的概率。
t=1时，可以利用初始概率(来自于P向量）和观察概率Pr(observation|state)（来自于混淆矩阵）计算局部概率；而t>1时的局部概率可以利用t-时的局部概率计算。
因此，这个问题是递归定义的，观察序列的概率就是通过依次计算t=1,2,…,T时的局部概率，并且对于t=T时所有局部概率‘s相加得到的。
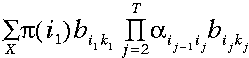
实践
testfor: 利用前向算法计算log Prob(观察序列| HMM模型)（Computes log Prob(observation|model) using the Forward algorithm.）
'/home/phoebe/Documents/umdhmm-v1.02/testfor' test.hmm test.seq
不知道为什么一定要用全的路径，否则无法找到testfor
就可以得到观察序列的概率结果的对数值，
首先，需要定义HMM的数据结构，也就是HMM的五个基本要素，在UMDHMM中是如下定义的（在hmm.h中）：
typedef struct
{
int M; /* 观察符号数目; V={1,2,…,M}*/dry damp soggy
int N; /* 隐藏状态数目;Q={1,2,…,N} */cloud sunny rain
double **A; /* 状态转移矩阵A[1..N][1..N]. a[i][j] 是从t时刻状态i到t+1时刻状态j的转移概率 */
double **B; /* 混淆矩阵B[1..N][1..M]. b[j][k]在状态j时观察到符合k的概率。*/
double *pi; /* 初始向量pi[1..N]，pi[i] 是初始状态概率分布 */
} HMM;
前向算法程序示例如下（在forward.c中）：
/*
函数参数说明：
*phmm：已知的HMM模型；T：观察符号序列长度；
*O：观察序列；**alpha：局部概率；*pprob：最终的观察概率
*/
void Forward(HMM *phmm, int T, int *O, double **alpha, double *pprob)
{
int i, j; /* 状态索引 */
int t; /* 时间索引 */
double sum; /*求局部概率时的中间值 */
/* 1. 初始化：计算t=1时刻所有状态的局部概率： */
for (i = 1; i <= phmm->N; i++)
alpha[1][i] = phmm->pi[i]* phmm->B[i][O[1]];
/* 2. 归纳：递归计算每个时间点，t=2，… ，T时的局部概率 */
for (t = 1; t < T; t++) { for (j = 1; j <= phmm->N; j++)
{
sum = 0.0;
for (i = 1; i <= phmm->N; i++)
sum += alpha[t][i]* (phmm->A[i][j]);
alpha[t+1][j] = sum*(phmm->B[j][O[t+1]]);
}
}
/* 3. 终止：观察序列的概率等于T时刻所有局部概率之和*/
*pprob = 0.0;
for (i = 1; i <= phmm->N; i++)
*pprob += alpha[T][i];
}
维特比算法
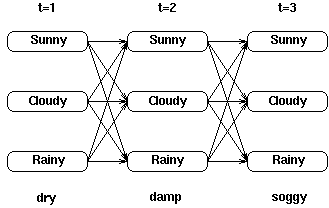
然而我们的目标是在给定一个观察序列的情况下寻找网格中最可能的隐藏状态序列——因此，我们需要一些方法来记住网格中的局部最佳路径。
就有可能记录前一时刻哪个状态生成了
(i,t).该状态导致了系统在t时刻到达状态i是最优的
这种记录（记忆）是通过对每一个状态赋予一个反向指针
完成的，这个指针指向最优的引发当前状态的前一时刻的某个状态。
形式上，我们可以写成如下的公式
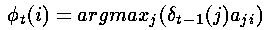
其中argmax运算符是用来计算使括号中表达式的值最大的索引j的。
请注意这个表达式是通过前一个时间步骤的局部概率‘s和转移概率计算的，并不包括观察概率（与计算局部概率‘s本身不同）。这是因为我们希望这些‘s能回答这个问题“如果我在这里，最可能通过哪条路径到达下一个状态？”——这个问题与隐藏状态有关，因此与观察概率有关的混淆（矩阵）因子是可以被忽略的。
2.维特比算法有一个非常有用的性质，就是对于观察序列的整个上下文进行了最好的解释（考虑）。事实上，寻找最可能的隐藏状态序列不止这一种方法，其他替代方法也可以，譬如，可以这样确定如下的隐藏状态序列：
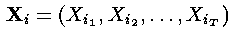
其中
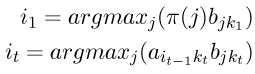（（a_i_(t-1)j是正确的）这个不是累计最优只是求每一步的最优，维特比则是全局最优
这里，采用了“自左向右”的决策方式进行一种近似的判断，其对于每个隐藏状态的判断是建立在前一个步骤的判断的基础之上（而第一步从隐藏状态的初始向量
开始）。
这种做法，如果在整个观察序列的中部发生“噪音干扰”时，其最终的结果将与正确的答案严重偏离。
相反， 维特比算法在确定最可能的终止状态前将考虑整个观察序列，然后通过指针“回溯”以确定某个隐藏状态是否是最可能的隐藏状态序列中的一员。这是非常有用的，因为这样就可以孤立序列中的“噪音”，而这些“噪音”在实时数据中是很常见的。
状态：sunny cloudy windy
观察：dry damp soggy
b_jk1 ：在状态j下观察到k1（由上面观察到下面的概率）
pi(j)：初始j状态的概率
ai_t-1 k_t:转移概率
argmaxi：求使得后面表达式最大的i
——（下面第一个公式）这一步是通过隐藏状态的初始概率和相应的观察概率之积计算了t=1时刻的局部概率。
对于t=2，…，T和i=1，…，n,令：
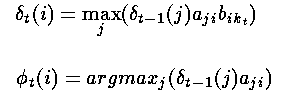算法对于每一个状态(t>1)都保存了一个反向指针()，并在每一个状态中存储了一个局部概率()。
——（上面第二公式）这样就确定了到达下一个状态的最可能路径，并对如何到达下一个状态做了记录
总结(Summary)
对于一个特定的隐马尔科夫模型，维特比算法被用来寻找生成一个观察序列的最可能的隐藏状态序列。我们利用概率的时间不变性，通过避免计算网格中每一条路径的概率来降低问题的复杂度。维特比算法对于每一个状态(t>1)都保存了一个反向指针()，并在每一个状态中存储了一个局部概率()。
局部概率是由反向指针指示的路径到达某个状态的概率。
当t=T时，维特比算法所到达的这些终止状态的局部概率‘s是按照最优（最可能）的路径到达该状态的概率。因此，选择其中最大的一个，并回溯找出所隐藏的状态路径，就是这个问题的最好答案。
关于维特比算法，需要着重强调的一点是它不是简单的对于某个给定的时间点选择最可能的隐藏状态，而是基于全局序列做决策——因此，如果在观察序列中有一个“非寻常”的事件发生，对于维特比算法的结果也影响不大。
这在语音处理中是特别有价值的，譬如当某个单词发音的一个中间音素出现失真或丢失的情况时，该单词也可以被识别出来。
个别的丢失不影响全局的情况。
维特比算法程序示例：
维特比算法程序示例如下（在viterbi.c中):
void Viterbi(HMM *phmm, int T, int *O, double **delta, int **psi,int *q, double *pprob)
{
int i, j; /* state indices */i和j分别代表后一个状态，前一个状态
int t; /* time index */时间序列
int maxvalind;状态记录标志
double maxval, val;
/* 1. Initialization */
for (i = 1; i <= phmm->N; i++)/隐藏的状态数目 sunny cloudy rainy
{
delta[1][i] = phmm->pi[i] * (phmm->B[i][O[1]]);//t=1时候的初始概率，B[i][o[1]]:在i状态下观察到o[1]的概率 “从上到下”
psi[1][i] = 0;//？
}
/* 2. Recursion */回溯
for (t = 2; t <= T; t++)
{
for (j = 1; j <= phmm->N; j++)//后一个状态j数目“3”
{
maxval = 0.0;
maxvalind = 1;
for (i = 1; i <= phmm->N; i++)//前一个状态i，数目3
{
val = delta[t-1][i]*(phmm->A[i][j]);//哪一i个到j是最优的
if (val > maxval)
{
maxval = val;
maxvalind = i;
}
}//for
delta[t][j] = maxval*(phmm->B[j][O[t]]);//记录概率值
psi[t][j] = maxvalind;//记录位置
}//for
}//for
/* 3. Termination */
*pprob = 0.0;
q[T] = 1;
for (i = 1; i <= phmm->N; i++)//确定最终的概率
{
if (delta[T][i] > *pprob)
{
*pprob = delta[T][i];
q[T] = i;
}
}
/* 4. Path (state sequence) backtracking */
for (t = T – 1; t >= 1; t–)//回溯路径
q[t] = psi[t+1][q[t+1]];
}
前向-后向算法1：
根据观察序列生成隐马尔科夫模型(Generating a HMM from a sequence of obersvations)
维特比算法：求解得到此观察序列的状态转移序列
向前算法：求此HMM 模型得到此观察序列的概率 ，目地：求得哪一个HMM最有可能产生了这个给定的观察序列
与HMM模型相关的“有用”的问题是评估（前向算法）和解码（维特比算法）——它们一个被用来测量一个模型的相对适用性，另一个被用来推测模型隐藏的部分在做什么（“到底发生了”什么）。
可以看出它们都依赖于隐马尔科夫模型（HMM）参数这一先验知识——
- 状态转移矩阵，**A
- 混淆（观察）矩阵**B，
- 以及pi向量（初始化概率向量）*pi
一个例子可能是一个庞大的语音处理数据库，其底层的语音可能由一个马尔可夫过程基于已知的音素建模的，而其可以观察的部分可能由可识别的状态（可能通过一些矢量数据表示）建模的，但是没有（直接）的方式来获取隐马尔科夫模型（HMM）参数。
之所以称其为前向-后向算法，主要是因为对于网格中的每一个状态，它既计算到达此状态的“前向”概率（给定当前模型的近似估计），又计算生成此模型最终状态的“后向”概率（给定当前模型的近似估计）。 这些都可以通过利用递归进行有利地计算，就像我们已经看到的。可以通过利用近似的HMM模型参数来提高这些中间概率进行调整，而这些调整又形成了前向-后向算法迭代的基础。
要理解前向-后向算法，首先需要了解两个算法：后向算法和EM算法。
后向算法是必须的，因为前向-后向算法就是利用了前向算法与后向算法中的变量因子，其得名也因于此；
而EM算法不是必须的，不过由于前向-后向算法是EM算法的一个特例，因此了解一下EM算法也是有好处的，说实话，对于EM算法，我也是云里雾里的。好了，废话少说，我们先谈谈后向算法。
1、后向算法（Backward algorithm）
其实如果理解了前向算法，后向算法也是比较好理解的，这里首先重新定义一下前向算法中的局部概率at(i)，称其为前向变量，这也是为前向-后向算法做点准备：
相似地，我们也可以定义一个后向变量Bt(i)（同样可以理解为一个局部概率）：
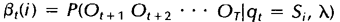
后向变量(局部概率)表示的是已知隐马尔科夫模型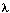
及t时刻位于隐藏状态Si这一事实，从t+1时刻到终止时刻的局部观察序列的概率。同样与前向算法相似，我们可以从后向前（故称之为后向算法）递归地计算后向变量：
1）初始化，令t=T时刻所有状态的后向变量为1：
2）归纳，递归计算每个时间点，t=T-1,T-2,…,1时的后向变量：
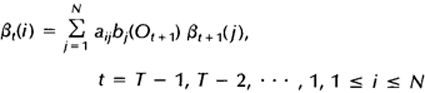
这样就可以计算每个时间点上所有的隐藏状态所对应的后向变量，如果需要利用后向算法计算观察序列的概率，只需将t=1时刻的后向变量（局部概率）相加即可。下图显示的是t+1时刻与t时刻的后向变量之间的关系：
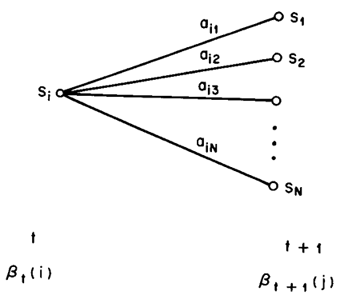
（此图为向前概率求法）
后向算法程序示例如下（在backward.c中):
void Backward(HMM *phmm, int T, int *O, double **beta, double *pprob)
{
int i, j; /* state indices */
int t; /* time index */
double sum;
/* 1. Initialization */
for (i = 1; i <= phmm->N; i++)
beta[T][i] = 1.0;
/* 2. Induction */
for (t = T - 1; t >= 1; t--)
{
for (i = 1; i <= phmm->N; i++)
{
sum = 0.0;
for (j = 1; j <= phmm->N; j++)
sum += phmm->A[i][j] *
(phmm->B[j][O[t+1]])*beta[t+1][j];
beta[t][i] = sum;
}
}
/* 3. Termination */
*pprob = 0.0;
for (i = 1; i <= phmm->N; i++)
*pprob += beta[1][i];
}
假定集合Z = (X,Y)由观测数据 X 和未观测数据Y 组成，Z = (X,Y)和 X 分别称为完整数据和不完整数据。假设Z的联合概率密度被参数化地定义为P(X，Y|Θ)，其中Θ 表示要被估计的参数。Θ 的最大似然估计是求不完整数据的对数似然函数L(X;Θ)的最大值而得到的：
L(Θ; X )= log p(X |Θ) = ∫log p(X ,Y |Θ)dY ；(1)
EM算法包括两个步骤：由E步和M步组成，它是通过迭代地最大化完整数据的对数似然函数Lc( X;Θ )的期望来最大化不完整数据的对数似然函数，其中：
Lc(X;Θ) =log p(X，Y |Θ) ； (2)
假设在算法第t次迭代后Θ 获得的估计记为Θ(t ) ，则在（t+1）次迭代时，
E-步：计算完整数据的对数似然函数的期望，记为：
Q(Θ |Θ (t) ) = E{Lc(Θ;Z)|X;Θ(t) }； (3)
M-步：通过最大化Q(Θ |Θ(t) ) 来获得新的Θ 。
通过交替使用这两个步骤，EM算法逐步改进模型的参数，使参数和训练样本的似然概率逐渐增大，最后终止于一个极大点。
直观地理解EM算法，它也可被看作为一个逐次逼近算法：事先并不知道模型的参数，可以随机的选择一套参数或者事先粗略地给定某个初始参数λ0 ，确定出对应于这组参数的最可能的状态，计算每个训练样本的可能结果的概率，在当前的状态下再由样本对参数修正，重新估计参数λ ，并在新的参数下重新确定模型的状态，这样，通过多次的迭代，循环直至某个收敛条件满足为止，就可以使得模型的参数逐渐逼近真实参数。
EM算法的主要目的是提供一个简单的迭代算法计算后验密度函数（在收到某个消息之后，接收端所了解到的该消息发送的概率称为后验概率。），它的最大优点是简单和稳定，但容易陷入局部最优。
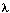，定义t时刻位于隐藏状态Si的概率变量为：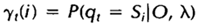
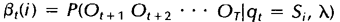
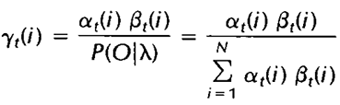
其中分母的作用是确保：
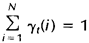
给定观察序列O及隐马尔科夫模型
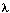，定义t时刻位于隐藏状态Si及t+1时刻位于隐藏状态Sj的概率变量为：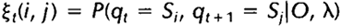
该变量在网格中所代表的关系如下图所示：
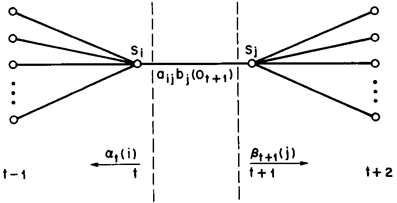
同样，该变量也可以由前向、后向变量表示：
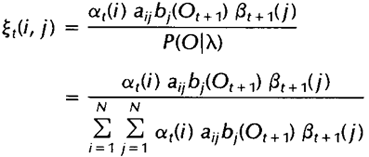
而上述定义的两个变量间也存在着如下关系：
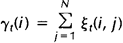
如果对于时间轴t上的所有
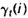相加，我们可以得到一个总和，它可以被解释为从其他隐藏状态访问Si的期望值（网格中的所有时间的期望），或者，如果我们求和时不包括时间轴上的t=T时刻，那么它可以被解释为从隐藏状态Si出发的状态转移期望值。相似地，如果对
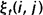在时间轴t上求和（从t=1到t=T-1），那么该和可以被解释为从状态Si到状态Sj的状态转移期望值。即：
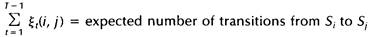
上一节我们定义了两个变量及相应的期望值，本节我们利用这两个变量及其期望值来重新估计隐马尔科夫模型（HMM）的参数pi，A及B：
如果我们定义当前的HMM模型为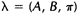
，那么可以利用该模型计算上面三个式子的右端；我们再定义重新估计的HMM模型为
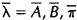，那么上面三个式子的左端就是重估的HMM模型参数。Baum及他的同事在70年代证明了
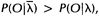因此如果我们迭代地的计算上面三个式子，由此不断地重新估计HMM的参数，那么在多次迭代后可以得到的HMM模型的一个最大似然估计。不过需要注意的是，前向-后向算法所得的这个结果（最大似然估计）是一个局部最优解。
关于前向-后向算法和EM算法的具体关系的解释，大家可以参考HMM经典论文《A tutorial on Hidden Markov Models and selected applications in speech recognition》，这里就不详述了。下面我们给出UMDHMM中的前向-后向算法示例，这个算法比较复杂，这里只取主函数，其中所引用的函数大家如果感兴趣的话可以自行参考UMDHMM
前向-后向算法程序示例如下（在baum.c中):
void BaumWelch(HMM *phmm, int T, int *O, double **alpha, double **beta, double **gamma, int *pniter, double *plogprobinit, double *plogprobfinal)
{
int i, j, k;
int t, l = 0;
double logprobf, logprobb, threshold;
double numeratorA, denominatorA;
double numeratorB, denominatorB;
double ***xi, *scale;
double delta, deltaprev, logprobprev;
deltaprev = 10e-70;
xi = AllocXi(T, phmm->N);
scale = dvector(1, T);
ForwardWithScale(phmm, T, O, alpha, scale, &logprobf);
*plogprobinit = logprobf; /* log P(O |intial model) */
BackwardWithScale(phmm, T, O, beta, scale, &logprobb);
ComputeGamma(phmm, T, alpha, beta, gamma);
ComputeXi(phmm, T, O, alpha, beta, xi);
logprobprev = logprobf;
do
{
/* reestimate frequency of state i in time t=1 */
for (i = 1; i <= phmm->N; i++)
phmm->pi[i] = .001 + .999*gamma[1][i];
/* reestimate transition matrix and symbol prob in
each state */
for (i = 1; i <= phmm->N; i++)
{
denominatorA = 0.0;
for (t = 1; t <= T - 1; t++)
denominatorA += gamma[t][i];
for (j = 1; j <= phmm->N; j++)
{
numeratorA = 0.0;
for (t = 1; t <= T - 1; t++)
numeratorA += xi[t][i][j];
phmm->A[i][j] = .001 +
.999*numeratorA/denominatorA;
}
denominatorB = denominatorA + gamma[T][i];
for (k = 1; k <= phmm->M; k++)
{
numeratorB = 0.0;
for (t = 1; t <= T; t++)
{
if (O[t] == k)
numeratorB += gamma[t][i];
}
phmm->B[i][k] = .001 +
.999*numeratorB/denominatorB;
}
}
ForwardWithScale(phmm, T, O, alpha, scale, &logprobf);
BackwardWithScale(phmm, T, O, beta, scale, &logprobb);
ComputeGamma(phmm, T, alpha, beta, gamma);
ComputeXi(phmm, T, O, alpha, beta, xi);
/* compute difference between log probability of
two iterations */
delta = logprobf - logprobprev;
logprobprev = logprobf;
l++;
}
while (delta > DELTA); /* if log probability does not
change much, exit */
*pniter = l;
*plogprobfinal = logprobf; /* log P(O|estimated model) */
FreeXi(xi, T, phmm->N);
free_dvector(scale, 1, T);
}
八、总结(Summary)
通常，模式并不是单独的出现，而是作为时间序列中的一个部分——这个过程有时候可以被辅助用来对它们进行识别。在基于时间的进程中，通常都会使用一些假设——一个最常用的假设是进程的状态只依赖于前面N个状态——这样我们就有了一个N阶马尔科夫模型。最简单的例子是N = 1。
存在很多例子，在这些例子中进程的状态（模式）是不能够被直接观察的，但是可以非直接地，或者概率地被观察为模式的另外一种集合——这样我们就可以定义一类隐马尔科夫模型——这些模型已被证明在当前许多研究领域，尤其是语音识别领域具有非常大的价值。
在实际的过程中这些模型提出了三个问题都可以得到立即有效的解决，分别是：
* 评估：对于一个给定的隐马尔科夫模型其生成一个给定的观察序列的概率是多少。前向算法可以有效的解决此问题。
* 解码：什么样的隐藏（底层）状态序列最有可能生成一个给定的观察序列。维特比算法可以有效的解决此问题。
* 学习：对于一个给定的观察序列样本，什么样的模型最可能生成该序列——也就是说，该模型的参数是什么。这个问题可以通过使用前向-后向算法解决。
隐马尔科夫模型（HMM）在分析实际系统中已被证明有很大的价值；它们通常的缺点是过于简化的假设，这与马尔可夫假设相关——即一个状态只依赖于前一个状态，并且这种依赖关系是独立于时间之外的（与时间无关）
