Biquads
From : http://www.earlevel.com/main/2003/02/28/biquads/
One of the most-used filter forms is the biquad. A biquad is a second order (two poles and two zeros) IIR filter. It is high enough order to be useful on its own, and—because of coefficient sensitivities in higher order filters—the biquad is often used as the basic building block for more complex filters. For instance, a biquad lowpass filter has a cutoff slope of 12 dB/octave, useful for tone controls; if you need a 24 dB/octave slope, you can cascade two biquads, and it will have less coefficient-sensitivity problems than a single fourth-order design.
Biquads come in several forms. The most obvious, a direct implementation of the second order difference equation (y[n] = a0*x[n] + a1*x[n-1] + a2*x[n-2] – b1*y[n-1] – b2*y[n-2]), called direct form I:
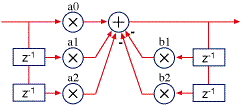 Direct form I
Direct form I
Direct form I is the best choice for implementation in a fixed point processor because it has a single summation point (fixed point DSPs usually have an extended accumulator that allows for intermediate overflows).
We can take direct form I and split it at the summation point like this:

We then take the two halves and swap them, so that the feedback half (the poles) comes first:
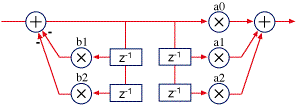
Now, notice that one pair of the z delays is redundant, storing the same information as the other. So, we can merge the two pairs, yielding the direct form II configuration:
 Direct form II
Direct form II
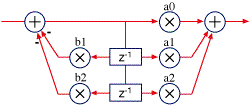
In floating point, direct form II is better because it saves two memory locations, and floating point is not sensitive to overflow in the way fixed point math is. We can improve this a little by transposing the filter. To transpose a filter, reverse the signal flow direction—output becomes input, distribution nodes become summers, and summers become nodes. The characteristics of the filter are unchanged, but in this case it happens that the floating point characteristics are a little better. Floating point has better accuracy when intermediate sums are with closer values (adding small numbers to large number in floating point is less precise than with similar values). Here is the transposed direct form II:
 Transposed direct form II
Transposed direct form II
Notes and recommendations
Again, direct form I is usually the best choice for fixed point, and transposed direct form II for floating point.
At low frequency settings, biquads are more susceptible to quantization error, mainly from the feedback coefficients (b1 and b2) and the delay memory. Lack of resolution in the coefficients makes precise positioning of the poles difficult, which is particularly a problem when the poles are positioned near the unit circle. The second problem, delay memory, is because multiplication generates more bits, and the bits are truncated when stored to memory. This quantization error is fed back in the filter, causing instability. 32-bit floating point is usually good enough for audio filters, but you may need to use double precision, especially at very low frequencies (for control filtering) and at high sample rates.
For fixed point filters, 24-bit coefficients and memory work well for most filters, but start to become unstable below about 300 Hz at 48 kHz sample rate (or twice that at 96 kHz). Double precision is always costly on a fixed point processor, but fortunately there is a simple technique for improving stability. Looking at the direct form I drawing, the quantization occurs when the higher precision accumulator is stored in the lower precision delay memory on the right side. By taking the quantization error (the difference between the full accumulated value and its value after storing it to memory) and adding it back in for the next sample calculation, the filter performs nearly as well as using full double precision calculations, but at a much lower computational cost. This technique is called first order noise shaping. There are higher order noise shapers, but this one works well enough to handle almost all audio needs, even at high sample rates.
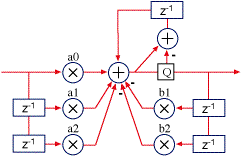 Direct form I with first-order noise shaping
Direct form I with first-order noise shaping
In general, 16-bit fixed point processing is not suitable for audio without double precision coefficients and computation.
Finally, biquads are just one of a DSP programmers tools—they aren’t always the best filter form. There are other filters that don’t share the biquad’s low-frequency sensitivities (in general, biquad coefficient precision is very good at high frequencies, and poor at low ones; there are other filter forms that spread the precision out more evenly, or trade off reduced high frequency performance for better low frequency performance). However, biquads are well known and design tools are plentiful, so they are usually the first choice for an IIR filter unless you find a reason to use another.
There are too many filter forms to cover, but one other filter form that is popular for synthesizers is the state variable filter. It has very excellent low frequency performance, and limitations in the high frequencies that have to be worked around, but most importantly frequency and Q coefficients are separate and easy to change for dynamic filtering. It also make a great low frequency sine wave generator.

