位操作实现四则运算

转载自新书《程序员面试笔试宝典》官网

参考《程序员面试笔试宝典》实现用位操作进行四则运算：

需要熟练掌握一些常见功能的位操作实现，具体为：

    <1> 常用的等式：-n = ~(n-1) = ~n+1

    <2> 获取整数n的二进制中最后一个1：n&(-n) 或者 n&~(n-1)，如：n=010100，则-n=101100，n&(-n)=000100

    <3> 去掉整数n的二进制中最后一个1：n&(n-1)，如：n=010100，n-1=010011，n&(n-1)=010000

 

(1)、加法实现

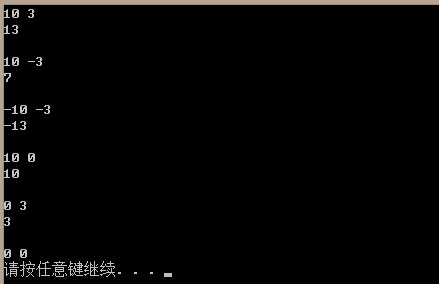
a + b，我们可以用 “异或” 运算来得到抛开进位的加法结果 add = a ^ b，然后用 "与" 和 "左移" 运算得到进位结果 carry = (a & b) << 1，再计算add + carry的值，如此就构成循环，只要carry的值不为0就一直循环下去。

int plus(int a, int b)
{
    if ((0 == a) || (0 == b))
    {
        return ((0 == a) ? b : a);
    }

    int add;
    int carry;

    while (0 != b)
    {
        add = a ^ b;
        carry = (a & b) << 1;

        a = add;
        b = carry;
    }

    return(a);
}

 

(2)、减法实现

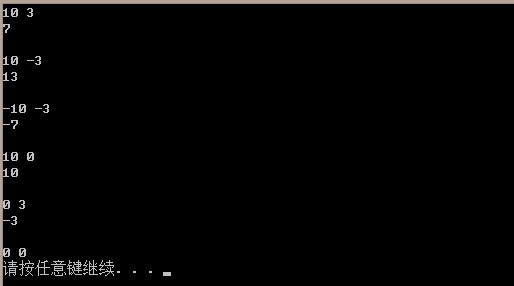
可以很容易的将减法运算转换为加法运算，a - b = a + (-b) = a + (~b) + 1。

int subtract(int a, int b)
{
    return (plus (a, plus (~b, 1)));
}

 

(3)、乘法实现

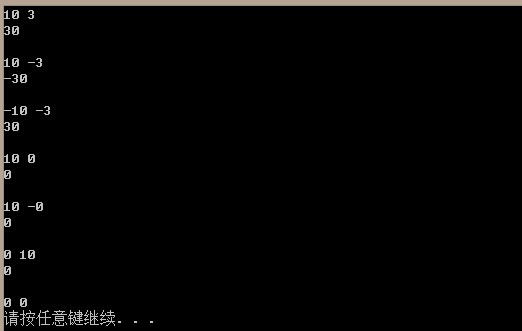
我有一篇博文提到二进制乘法的原理，这里将其转换成代码即可：

int multiply(int a, int b)
{
    if ((0 == a) || (0 == b))
    {
        return (0);
    }

    bool bFlag = (b < 0);

    if (b < 0)
    {
        b = -b;
    }

    int nAdd = 0;
    int nLast;
    int nFlag = 1;

    while (0 != b)
    {
        nLast = b & (-b);
        nFlag = 1;

        while (nFlag != nLast)
        {
            a <<= 1;
            nFlag <<= 1;
        }

        nAdd = plus (nAdd, a);
        b &= subtract (b, 1);
    }

    return (bFlag ? (-nAdd) : nAdd);
}

 

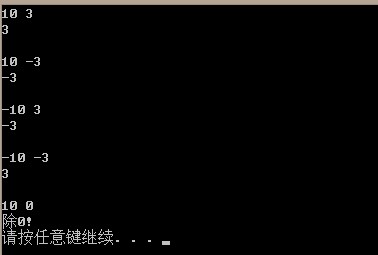
(4)、除法实现

 除法就是由乘法的过程逆推，依次减掉（如果x够减的）y^(2^31),y^(2^30),...y^8,y^4,y^2,y^1。减掉相应数量的y就在结果加上相应的数量。

int divide(int a,int b)
{
    if (0 == b)
    {
        printf ("除0!\n");
        exit(-1);
    }

    bool bFlag = (a < 0) ^ (b < 0);

    if (a < 0)
    {
        a = -a;
    }

    if (b < 0)
    {
        b = -b;
    }

    int ans=0;
    for(int i=31;i>=0;i--)
    {
        // 比较x是否大于y的(1<<i)次方，避免将x与(y<<i)比较，因为不确定y的(1<<i)次方是否溢出
        if((a >> i) >= b)
        {
            ans =plus (ans, (1<<i));
            a = subtract(a, (b << i));
        }
    }

    return (bFlag ? (-ans) : ans);
}