将二分搜索树转变成排序的双向链表

二分搜索树的数据结构为：

struct BinaryTreeNode
{
    int nValue;

    BinaryTreeNode *pLeft;
    BinaryTreeNode *pRight;
};

首先我们来通过一个简单的例子来获取直接的感官，将这颗排序二叉树

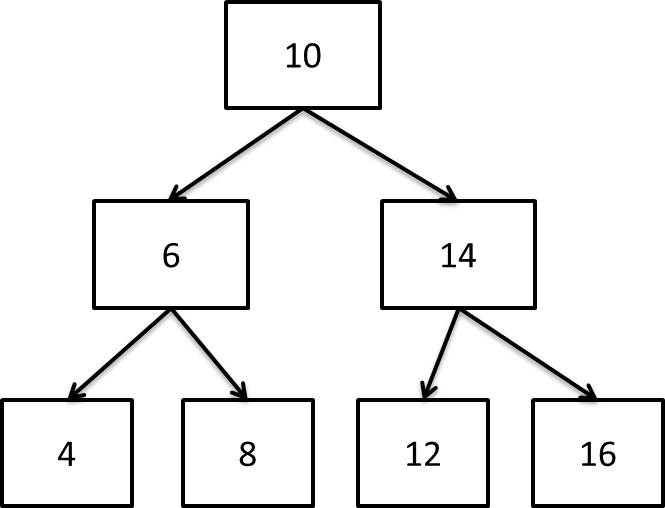
转变为排序的双向链表应为：

可以很清楚的发现转换完成的双向链表的顺序其实就是二叉搜索树的中序遍历的顺序，因此这个题我们可以借助中序遍历来完成。因为二叉树的结构很符合递归的思想，因此基本上所有关于二叉树的问题都可以用递归来完成，这个问题也不例外。我们假设中序遍历到达根节点10时，它的左子树已经转换成了排序双向链表，并且处在链表最末端的节点时链表中值最大的节点（即8），我们将这个节点和根节点10连接起来，则10成为了链表中的最后一个节点。然后利用跟左子树同样的思想，将右子树转换成排序双向链表并将其连接在10的后面，则整个转换过程完成。

基于以上分析，可以写出下面代码：

BinaryTreeNode *Convert(BinaryTreeNode *pRootOfTree)
{
    assert (pRootOfTree != NULL);

    BinaryTreeNode *pLastNodeInList = NULL;

    ConvertNode (pRootOfTree, &pLastNodeInList);

    // pLastNodeInList指向双向链表尾结点
    // 我们需要返回头结点
    BinaryTreeNode *pHeadOfList = pLastNodeInList;

    while ((pHeadOfList != NULL) && (pHeadOfList->pLeft != NULL))
    {
        pHeadOfList = pHeadOfList->pLeft;
    }

    return (pHeadOfList);
}

ConvertNode函数的实现：

void ConvertNode(BinaryTreeNode *pNode, BinaryTreeNode **pLastNodeInList)
{
    assert (pLastNodeInList != NULL);

    if (NULL == pNode)
    {
        return;
    }

    BinaryTreeNode *pCurrent = pNode;

    // 理解递归算法的核心就是我们要相信它能完成我们给它假设的任务
    // 那么在这里我们就要相信pCurrent的左子树已经被转换成了一个排序的双向链表
    // ，并且pLastNodeInList指向了这个链表的最后一个节点
    if (pCurrent->pLeft != NULL)
    {
        ConvertNode (pCurrent->pLeft, pLastNodeInList);
    }

    // 接下来的任务就是将pCurrent这个节点加入这个链表的末尾
    // 首先将pCurrent的左指针指向这个链表的最后一个节点
    pCurrent->pLeft = *pLastNodeInList;

    if (*pLastNodeInList != NULL)
    {
        // 然后若这个链表不为空，即pCurrent不是链表的首节点
        // ，那么我们还需要将链表末尾节点的右指针指向pCurrent，才算完整的将pCurrent节点连入到链表的末尾
        (*pLastNodeInList)->pRight = pCurrent;
    }

    // 更新pLastNodeInList指针的指向，使其始终指向链表的最后一个节点
    *pLastNodeInList = pCurrent;

    if (pCurrent->pRight != NULL)
    {
        // 如果pCurrent的右子树不为空，则按照左子树的方式来处理右子树
        ConvertNode (pCurrent->pRight, pLastNodeInList);
    }
}