p1324 dining(晚餐)
题目描述:
农夫JOHN为牛们做了很好的食品,但是牛吃饭很挑食. 每一头牛只喜欢吃一些食品和饮料而别的一概不吃.虽然他不一定能把所有牛喂饱,他还是想让尽可能多的牛吃到他们喜欢的食品和饮料.
农夫JOHN做了F (1 <= F <= 100) 种食品并准备了D (1 <= D <= 100) 种饮料. 他的N (1 <= N <= 100)头牛都以决定了是否愿意吃某种食物和喝某种饮料. 农夫JOHN想给每一头牛一种食品和一种饮料,使得尽可能多的牛得到喜欢的食物和饮料.
每一件食物和饮料只能由一头牛来用. 例如如果食物2被一头牛吃掉了,没有别的牛能吃食物2.
输入格式 Input Format
* 第一行: 三个数: N, F, 和 D
* 第2..N+1行: 每一行由两个数开始F_i 和 D_i, 分别是第i 头牛可以吃的食品数和可以喝的饮料数.下F_i个整数是第i头牛可以吃的食品号,再下面的D_i个整数是第i头牛可以喝的饮料号码.
输出格式 Output Format
* 第一行: 一个整数,最多可以喂饱的牛数.
样例输入 Sample Input
4 3 3
2 2 1 2 3 1
2 2 2 3 1 2
2 2 1 3 1 2
2 1 1 3 3
输入解释:
牛 1: 食品从 {1,2}, 饮料从 {1,3} 中选
牛 2: 食品从 {2,3}, 饮料从 {1,2} 中选
牛 3: 食品从 {1,3}, 饮料从 {1,2} 中选
牛 4: 食品从 {1,3}, 饮料从 {3} 中选
样例输出 Sample Output
3
输出解释:
一个方案是:
Cow 1: 不吃
Cow 2: 食品 #2, 饮料 #2
Cow 3: 食品 #1, 饮料 #1
Cow 4: 食品 #3, 饮料 #3
用鸽笼定理可以推出没有更好的解 (一共只有3总食品和饮料).当然,别的数据会更难.
时间限制 Time Limitation
1s
这道题就是一个最大流的题就是看你怎么建图了,因为一头奶牛它可能有许多喜欢的食物(这奶牛吃的怪好)
所以你就不能直接从原点--食物--奶牛--饮料--终点,如果这样就意味着奶牛会吃的超过一种食物和饮料,
所以就把奶牛拆成两个点,两个点的容量为1,一个点连食物,一个连饮料就行了。
截图.jpg
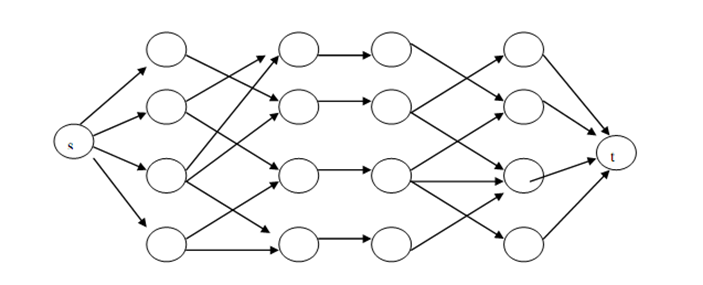
代码如下:

1 #include<iostream> 2 #include<cstdio> 3 #include<cmath> 4 #include<algorithm> 5 #include<cstring> 6 using namespace std; 7 int n,f,d; 8 int a[4000][4000]; 9 bool vis[4000],check=true; 10 int s; 11 int sum=0,forword; 12 void dfs(int k,int l) 13 { 14 vis[k]=true; 15 if(k==s) 16 { 17 check=true; 18 sum+=l; 19 forword=l; 20 return; 21 } 22 for(int i=1;i<=s;i++) 23 { 24 if((a[k][i]>0)&&(!vis[i])) 25 { 26 dfs(i,min(a[k][i],l)); 27 if(check) 28 { 29 a[k][i]-=forword; 30 a[i][k]+=forword; 31 return; 32 } 33 } 34 } 35 } 36 int main() 37 { 38 scanf("%d%d%d",&n,&f,&d); 39 for(int i=1;i<=f;i++)//从原点连到食物 40 { 41 a[1][i+1]=1; 42 } 43 for(int i=1;i<=n;i++)//奶牛拆成两点后自己连自己 44 a[f+1+i][f+1+n+i]=1; 45 for(int i=1;i<=n;i++) 46 { 47 int x,y; 48 scanf("%d%d",&x,&y); 49 for(int j=1;j<=x;j++)//食品 50 { 51 int q; 52 scanf("%d",&q); 53 a[1+q][i+f+1]=1; 54 } 55 for(int j=1;j<=y;j++)//饮料 56 { 57 int q; 58 scanf("%d",&q); 59 a[n+i+1+f][2*n+f+1+q]=1; 60 } 61 } 62 s=f+d+2*n+2; 63 for(int i=1;i<=d;i++)//最后连到终点 64 { 65 a[2*n+f+1+i][s]=1; 66 } 67 while(check) 68 { 69 check=false; 70 memset(vis,false,sizeof(vis)); 71 dfs(1,10000); 72 } 73 cout<<sum<<endl; 74 return 0; 75 }



