HNOI2018省队集训 Day4&5
HNOI2018省队集训 Day4&5
Day4很毒,先鸽了(HN队长都鸽了,所以不能怪我)
marshland
前方有一片沼泽地.
方便地, 我们用一个 n × n 的网格图来描述它, 每一个格子代表着沼泽地 的一小片区域. 其中 (1, 1) 代表网格图的左上角, (n, n) 代表网格图的右下角. 若用 X 表示行数, Y 表示列数, 那么 X + Y 为奇数的格子有一个危险度 VX,Y , X + Y 为偶数的格子的危险度为 0.
为了保障人们的安全, 你有 m 个长相怪异的大石头, 你可以选一些石头 放在网格图上的某些格子上, 石头可以看成一个 ‘L’ 形的块, 并且占三个格子, 它通过旋转有四种方式供放置, 仅会使得在拐角处的那个格子危险度减为 0.
网格图中还有 k 个位置是 “禁止位置”, 石头的任何部位都不能位于这些 格子上, 且这些位置的危险度一定为 0.
现在你需要知道放置一些石头后最小的危险度之和是多少. (石头可以不放完)
考虑费用流,最开始我考虑的是把选择每个石头抽象成点,有个常见的建法:
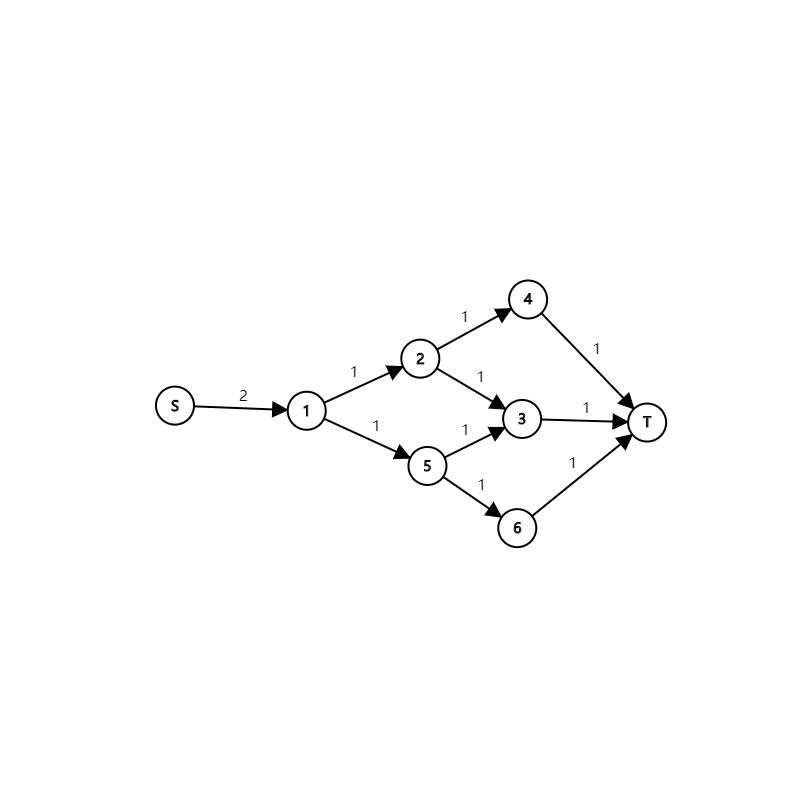
这样4、3里面只能选一个,3、6里面只能选一个,并且436每个最多选一次,貌似很符合这道题。但是这道题的每个限制是选了一个其他的无法再选,显然这样的模型无法保证(1-5-6,1-2-3)。
那么考虑对于每个点只能选一次这个限制和每个点属于哪个L形,容易发现L形可以被拆分为三个点:奇数列的偶数行点,奇数列的奇数行点,偶数列的偶数行点。这么做我们就只需要用上面的模型的后半部分(每个点被选一次),建立三排点。而且由于这些点行数和列数的奇偶性不一样,这样做就是对的。
关于计算答案,只需要把中间的点拆开加上一条(-w,1)的边即可。
注意跑费用流的时候不能dfs多路增广,需要找一条增广路增广,保证最大流每次+1,流到m或者答案不再减少直接退出即可。
party
显然party会在LCA出召开,每个点选的范围就是当前点到LCA的路径。
那么我们可以用\(O(n\frac m \omega)\)树剖+线段树建立,\(O(qc\log n\frac m \omega)\)查询每个询问中每个点可选集合。
对于每个询问怎么求答案呢?考虑到每个权值只能被选一次,题解告诉我们可以用二分图+Hall定理做。
Hall定理:二分图G存在完美匹配当且仅当X中的任意k个点至少与Y中的k个点相邻
我们可以\(2^c\frac m \omega\)求出当前点的集合可选权值种类的并集\(f(S)\) (注意这里可以递推来减少常数),然后对于每个集合\(|S|\)考虑k。因为答案一定是\(c*x\)的形式,就可以构造一个左边\(|S|*x\)个点,右边\(f(S)\)个点的二分图。 首先对于\(k=|S|*x\),\(x\)最大为 \(\frac{f(S)}{|S|}\),因为由于\(f(S)\)的定义左边的点和右边一定是完全联通的,只要总数\(|S|*x\leq f(S)\)即可。然后对于其他的至少含有 这个集合的每个点的 左边的x个点中的一个点 的k值的条件一定可以通过构造得到(去掉一些点)。那么总的x的最大值就是满足每个条件的最大值的最小值。
总复杂度\(O(n\frac m w+qc\log n\frac m w+q2^c\frac m w)\)
最开始写T了,因为没有预处理到链顶的答案。这在没有修改的题好像是常规操作,然而我一直用的是log^2...
platform
切了...但是要注意本质不同的子串算不算,我以为是算的,结果WA了一发。要仔细读题和样例解释!
考虑左端点相同的子串,右端点增大,权值和不减,降序排名单增(前面的串是后面的前缀)。那么2-1仍然单增,二分找到差值\(\leq 0\)的最后一个,判断是否等于0(相等)即可。
快速找子串排名我用的是反串的SAM的parent树上倍增+预处理出这个节点取到len最大的排名。具体加边方法画个SAM就知道了。总复杂度\(n\log^2n\),勉强卡过。
然后题解前半部分跟我是一样的,后半部分SA能做到\(\log n\),是用线段树维护区间赋值和加等差数列,SAM就暴力许多。
贴个代码吧:
#include<bits/stdc++.h>
#define FOR(i,a,b) for(int i=a;i<=b;++i)
#define ROF(i,a,b) for(int i=a;i>=b;--i)
#define ll long long
using namespace std;
const int N = 4e5+200;
int read(){
int x=0,pos=1;char ch=getchar();
for(;!isdigit(ch);ch=getchar()) if(ch=='-') pos=0;
for(;isdigit(ch);ch=getchar()) x=(x<<1)+(x<<3)+ch-'0';
return pos?x:-x;
}
char s[N];int n,w[N],pos[N],f[N][20];
ll val[N],vs[N],rk[N];
int las=1,tot=1;
struct typ{
int ch[26],fa,len,pos;
typ(){
memset(ch,0,sizeof(ch));fa=len=0;
}
}t[N];
#define pii pair<int,int>
#define fi first
#define se second
#define mp make_pair
vector<pii> edge[N];
void insert(int c,int id){
int p=las,np=las=++tot;pos[id]=np;w[np]=1;t[np].pos=id;
t[np].len=t[p].len+1;
for(;p&&!t[p].ch[c];p=t[p].fa) t[p].ch[c]=np;
if(!p){
t[np].fa=1;
}else{
int q=t[p].ch[c];
if(t[p].len+1==t[q].len) t[np].fa=q;
else{
int nq=++tot;
t[nq]=t[q];
t[nq].len=t[p].len+1,t[q].fa=t[np].fa=nq;
for(;t[p].ch[c]==q;p=t[p].fa) t[p].ch[c]=nq;
}
}
}
int ti[N],lnk[N];
ll rn=0;
void dfs1(int now){
for(int i=0;i<edge[now].size();i++){
int v=edge[now][i].se;
dfs1(v),w[now]+=w[v];if(!t[i].pos) t[i].pos=t[v].pos;
}
}
int cmp(pii a,pii b){
return a.fi>b.fi;
}
void dfs(int now){
sort(edge[now].begin(),edge[now].end(),cmp);
for(int i=0;i<edge[now].size();i++){
int v=edge[now][i].se;
dfs(v);
}
rk[now]=rn;
rn+=1ll*(t[now].len-t[t[now].fa].len);//*w[now];
}
ll calcrk(int l,int r){
int len=r-l+1,x=pos[l];
ROF(i,19,0){
if(t[f[x][i]].len>=len) x=f[x][i];
}
return 1ll+rk[x]+1ll*(t[x].len-len);//*w[x];
}
ll calcv(int l,int r){
return vs[r]-vs[l-1];
}
ll calc(int l,int r){
return calcv(l,r)-calcrk(l,r);
}
vector<pii> ans;
int main(){
scanf("%s",s+1);
n=strlen(s+1);
FOR(i,1,n){
val[i]=read();vs[i]=vs[i-1]+val[i];
}
ROF(i,n,1){
insert(s[i]-'a',i);
}
FOR(i,2,tot){
f[i][0]=t[i].fa;
edge[t[i].fa].push_back({0,i});
}
dfs1(1);
FOR(i,1,tot) edge[i].clear();
FOR(i,2,tot){
edge[t[i].fa].push_back({s[t[i].pos+t[t[i].fa].len]-'a',i});
}
dfs(1);
FOR(i,1,19){
FOR(j,1,tot){
f[j][i]=f[f[j][i-1]][i-1];
}
}
FOR(i,1,n){
int l=i,r=n+1;
while(l<r-1){
int mid=(l+r)>>1;
if(calc(i,mid)<=0) l=mid;
else r=mid;
}
if(calc(i,l)==0){
ans.push_back({i,l});
}
}
printf("%d\n",ans.size());
if(!ans.size()) return 0;
FOR(i,0,ans.size()-1){
printf("%d %d\n",ans[i].fi,ans[i].se);
}
return 0;
}


