WQS二分学习笔记
WQS二分学习笔记
我们要求n个物品的dp，有选其中m个的限制，一般情况下是\(O(nm)\)，因为状态数是这么多，wqs二分可以去掉一些状态。
令\(f(i,j)\)为i个物品选j个的最大值，\(g(j)\)表示强制选j个的最大值，如果\(g(j)\)关于j的斜率单调不增/不减则可以wqs二分
下图是一个上凸包：
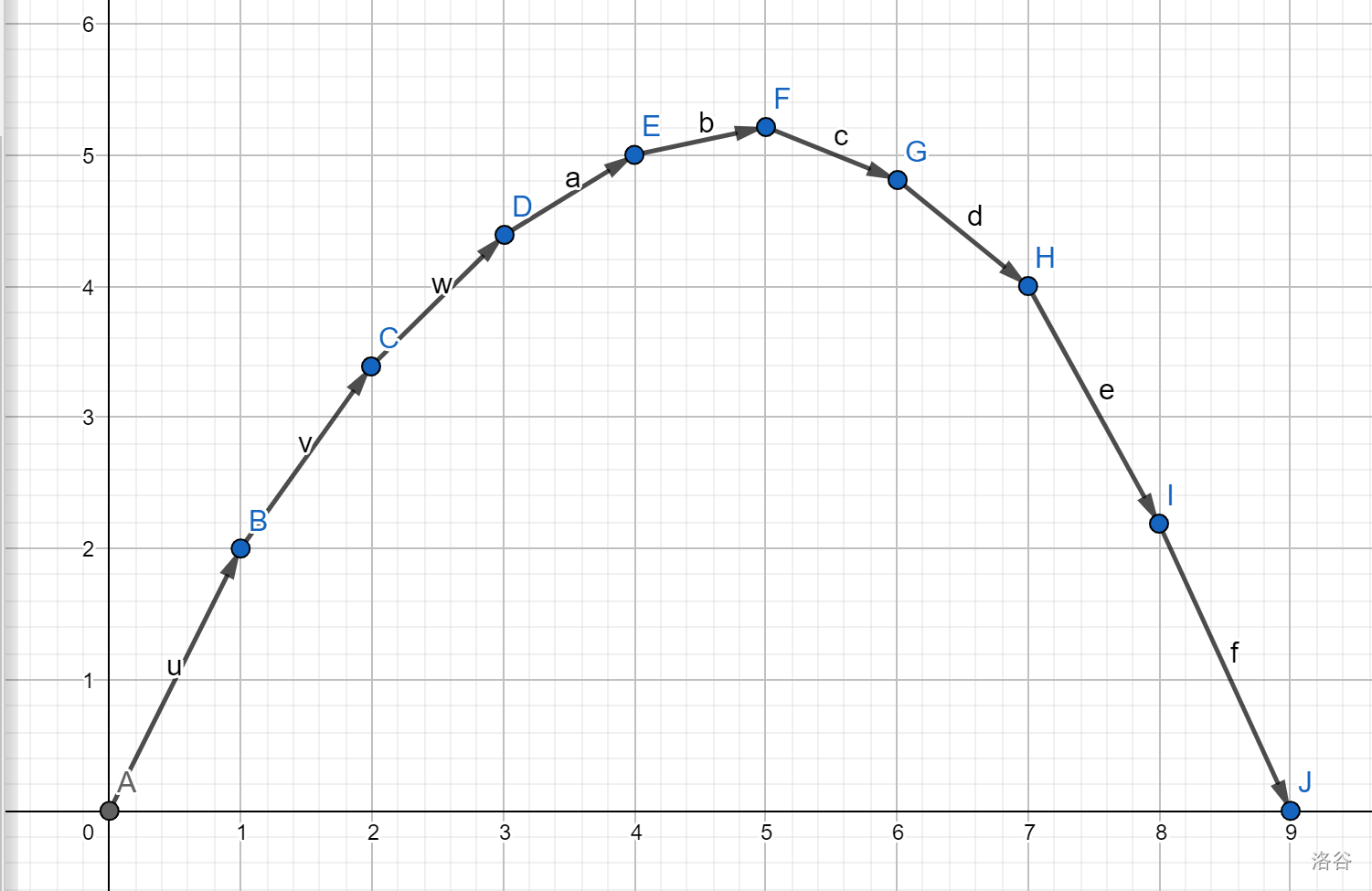
假如m=7，我们要使j=7。但是我们不知道这个g数组，我们考虑二分一条线去切这个凸包得到j=7的答案。具体方法是二分斜率k，如下图：
而且注意到切点也随k同增同减，我们就可以通过判断切点是否<=m来判断合法性了。
那么我们算出这种情况下每个点的截距，则切点的截距最大。下图E点截距最大
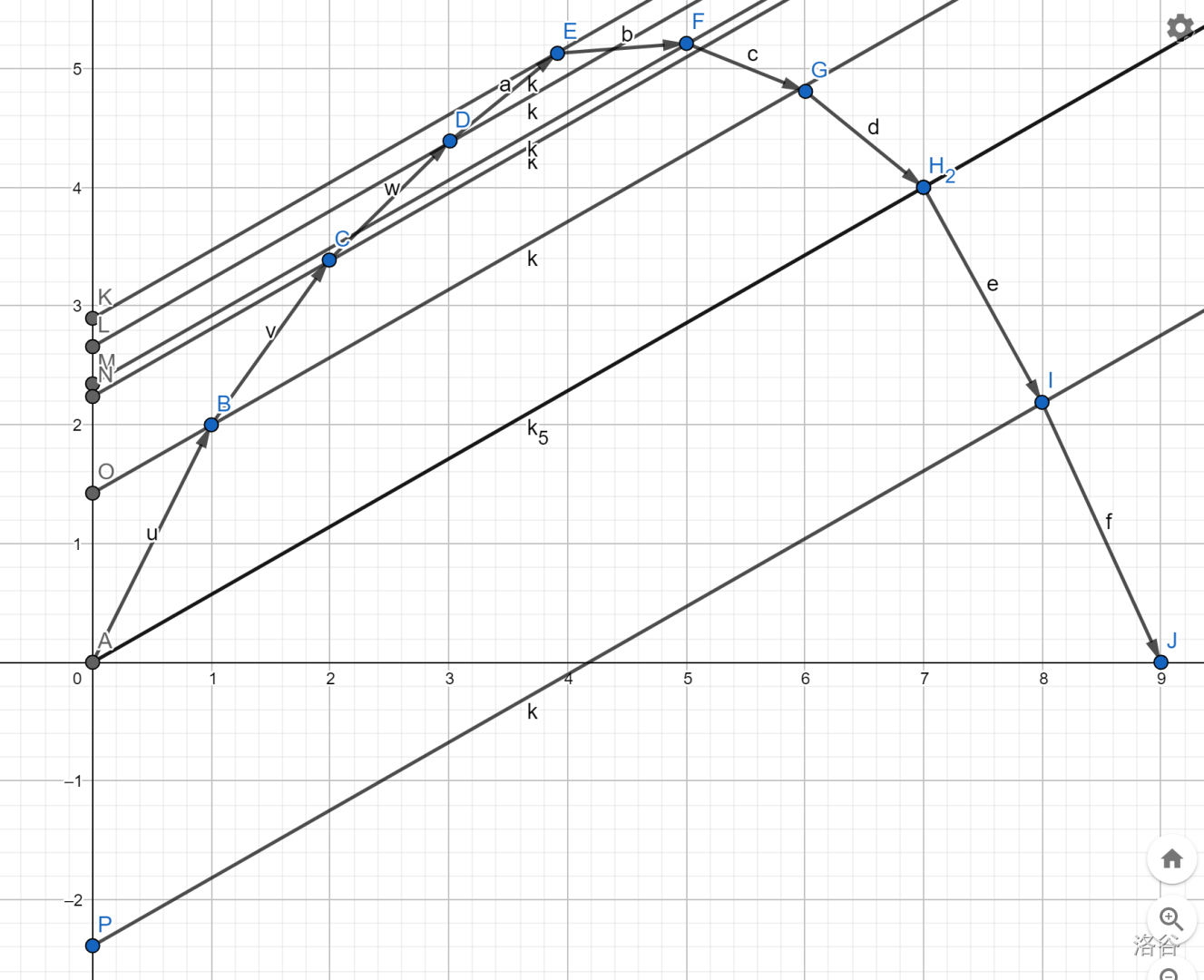
怎么计算答案呢？考虑截距\(kx+b=y\)，则\(b=y-kx\)。我们先把每个数的权值都减去\(k\)，那么取了 \(x\) 个数总权值就减去了 \(kx\) 。然后再做一遍没有限制个数的dp（一般是\(O(n)\)）求出切点和答案，然后通过切点判断往左还是往右就行了。最后一定能二分到m。注意有斜率相等的情况，或者有取不到m的情况，在所有最优结果中返回最左边的，也就是让 \(j\) 尽量小就行了，我们就可以通过这个点的答案推出m的答案。不能整体减k的时候，也可以在dp的时候每次直接减去这个k。
例题
luogu2619
通过打表观察可以发现选\(i\)条白色边的答案是一个下凸函数。感性理解，二分的斜率越大，白边数量一定增多，那么就是一个下凸壳。
loj3132
不考虑k的限制，\(f_i=\max_{j<i}(f_j+\frac{i-j}{i})\)
然后列出斜率优化式子：
\[f_k+\frac{i-k}{i}<f_j+\frac{i-j}{i}
\]
\[(f_j-f_k)\times i> j-k
\]
\[\frac{f_j-f_k}{j-k}>\frac 1 i
\]
那么加上WQS二分就行了。
PS:打表可得是个上凸壳
10 10
1.00000 1.00000 1.00000 1.00000 1.00000 1.00000 1.00000 1.00000 1.00000 1.00000
1.00000 1.50000 1.50000 1.50000 1.50000 1.50000 1.50000 1.50000 1.50000 1.50000
1.00000 1.66667 1.83333 1.83333 1.83333 1.83333 1.83333 1.83333 1.83333 1.83333
1.00000 1.75000 2.00000 2.08333 2.08333 2.08333 2.08333 2.08333 2.08333 2.08333
1.00000 1.80000 2.10000 2.23333 2.28333 2.28333 2.28333 2.28333 2.28333 2.28333
1.00000 1.83333 2.16667 2.33333 2.41667 2.45000 2.45000 2.45000 2.45000 2.45000
1.00000 1.85714 2.23810 2.42857 2.51905 2.56905 2.59286 2.59286 2.59286 2.59286
1.00000 1.87500 2.29167 2.50000 2.60833 2.66667 2.70000 2.71786 2.71786 2.71786
1.00000 1.88889 2.33333 2.55556 2.67778 2.75000 2.79127 2.81508 2.82897 2.82897
1.00000 1.90000 2.36667 2.60000 2.73333 2.81905 2.86905 2.90000 2.91786 2.92897
因为分的段越多新增段分母就越大，加的越来越慢。
同时复习了斜率优化，贴个代码：
- 斜率优化，\(i<j,slope(i,j)=\frac{Y(j)-Y(i)}{j-i}\)
- \(slope(i,j)>k,k单减\)，上凸壳+单调队列（双端）
- \(slope(i,j)>k,k单增\)，上凸壳+单调栈
- \(slope(i,j)<k,k单减\)，下凸壳+单调栈
- \(slope(i,j)<k,k单增\)，下凸壳+单调队列（双端）
- 考试的时候可以手推对于不同范围的斜率凸壳上三个点哪个比较优，来判断上下凸壳。
#include<bits/stdc++.h>
#pragma GCC optimize(2)
using namespace std;
#define ll long long
int read(){
int x=0,pos=1;char ch=getchar();
for(;!isdigit(ch);ch=getchar()) if(ch=='-') pos=0;
for(;isdigit(ch);ch=getchar()) x=(x<<1)+(x<<3)+ch-'0';
return pos?x:-x;
}
const double eps = 1e-15;
int n,m;
double ans=0,mid,f[100021];
int t,h;
int q[100021],g[100021];
double slope(int a,int b){
return (f[b]-f[a])/(1.0*(b-a));
}
int check(){
memset(f,0,sizeof(f));t=1,h=1;q[1]=0;memset(g,0,sizeof(g));
for(int i=1;i<=n;i++){
while(h<t&&slope(q[h],q[h+1])>(1.0/(1.0*i)+eps)) h++;
f[i]=f[q[h]]+(1.0*(i-q[h])/(1.0*i))-mid;g[i]=g[q[h]]+1;
while(h<t&&slope(q[t-1],q[t])<slope(q[t],i)-eps) t--;
q[++t]=i;
}
return g[n]>=m;
}
int main(){
n=read(),m=read();
double l=0,r=1;
while(l<r-eps){
mid=(l+r)/2.0;
if(check()) l=mid,ans=f[n];
else r=mid;
}
printf("%.10f",ans+m*l);
return 0;
}
九省联考2018 林克卡特树
考虑是上凸壳还是下凸壳，枚举的斜率k越小，边的权值越大，链的条数越来越小，切点向左移，先猜一个下凸壳。（懒得打表）
结果是对的
#include<iostream>
#include<algorithm>
#include<cstdio>
#include<cstring>
#define ll long long
using namespace std;
int read(){
int x=0,pos=1;char ch=getchar();
for(;!isdigit(ch);ch=getchar()) if(ch=='-') pos=0;
for(;isdigit(ch);ch=getchar()) x=(x<<1)+(x<<3)+ch-'0';
return pos?x:-x;
}
const int N = 3e5+200;
struct node{
int v,nex;ll w;
}edge[N*2];
int head[N],top=0;
void add(int u,int v,ll w){
edge[++top].w=w;
edge[top].v=v;
edge[top].nex=head[u];
head[u]=top;
}
ll mid=0;
int n,k;
struct typ{
ll f;int g;
typ(ll f=0,int g=0):f(f),g(g){}
friend typ operator + (typ a,typ b){
return typ(a.f+b.f,a.g+b.g);
}
friend int operator <(typ a,typ b){
return a.f==b.f?a.g<b.g:a.f<b.f;
}
friend typ operator + (typ a,int b){
return typ(a.f+b,a.g);
}
}dp[N][3];
typ del;
inline void ch(typ &a,typ b){
if(a<b) a=b;
}
void dfs(int now,int pre){
ch(dp[now][2],del);
for(int i=head[now];i;i=edge[i].nex){
int v=edge[i].v;if(v==pre) continue;dfs(v,now);
ch(dp[now][2],max(dp[now][2]+dp[v][0],dp[now][1]+dp[v][1]+del+edge[i].w));
ch(dp[now][1],max(dp[now][1]+dp[v][0],dp[now][0]+dp[v][1]+edge[i].w));
ch(dp[now][0],dp[v][0]+dp[now][0]);
}
ch(dp[now][0],max(dp[now][1]+del,dp[now][2]));
}
int check(){
memset(dp,0,sizeof(dp));
del=typ(-mid,1);
dfs(1,0);
return dp[1][0].g>=k;
}
int main(){
n=read(),k=read();k++;
for(int i=1;i<n;i++){
int u=read(),v=read(),w=read();
add(u,v,w);add(v,u,w);
}
ll l=-1e12,r=1e12;
ll ans=0;
while(l<r-1){
mid=(l+r)>>1;
if(check()){
l=mid,ans=dp[1][0].f;
if(dp[1][0].g==k) break;
}
else r=mid;
}
printf("%lld",ans+1ll*k*l);
return 0;
}
